Question Number 45827 by byaw last updated on 17/Oct/18

Commented by MJS last updated on 17/Oct/18

$$\mathrm{the}\:\mathrm{source}\:\mathrm{of}\:\mathrm{these}\:\mathrm{questions}\:\mathrm{is}\:\mathrm{at}\:\mathrm{least}\:\mathrm{not} \\ $$$$\mathrm{accurate},\:\mathrm{always}\:\mathrm{something}\:\mathrm{missing}\:\mathrm{or}\:\mathrm{other} \\ $$$$\mathrm{mistakes} \\ $$
Answered by hassentimol last updated on 17/Oct/18
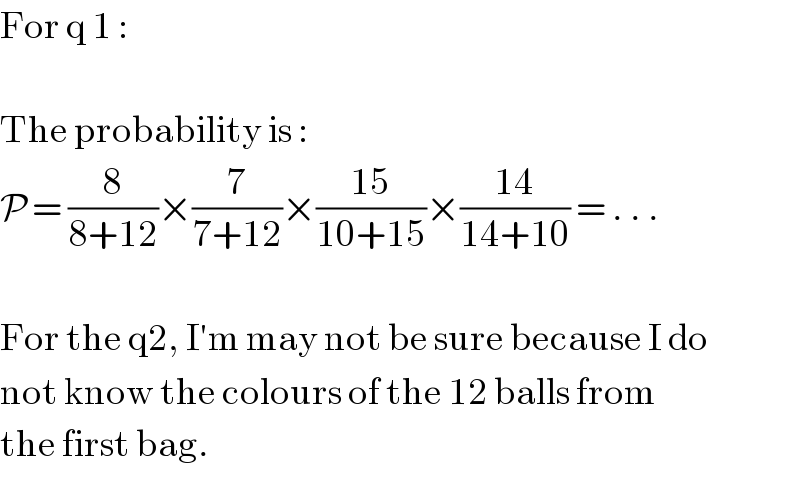
$$\mathrm{For}\:\mathrm{q}\:\mathrm{1}\:: \\ $$$$ \\ $$$$\mathrm{The}\:\mathrm{probability}\:\mathrm{is}\:: \\ $$$$\mathcal{P}\:=\:\frac{\mathrm{8}}{\mathrm{8}+\mathrm{12}}×\frac{\mathrm{7}}{\mathrm{7}+\mathrm{12}}×\frac{\mathrm{15}}{\mathrm{10}+\mathrm{15}}×\frac{\mathrm{14}}{\mathrm{14}+\mathrm{10}}\:=\:.\:.\:. \\ $$$$ \\ $$$$\mathrm{For}\:\mathrm{the}\:\mathrm{q2},\:\mathrm{I}'\mathrm{m}\:\mathrm{may}\:\mathrm{not}\:\mathrm{be}\:\mathrm{sure}\:\mathrm{because}\:\mathrm{I}\:\mathrm{do} \\ $$$$\mathrm{not}\:\mathrm{know}\:\mathrm{the}\:\mathrm{colours}\:\mathrm{of}\:\mathrm{the}\:\mathrm{12}\:\mathrm{balls}\:\mathrm{from} \\ $$$$\mathrm{the}\:\mathrm{first}\:\mathrm{bag}. \\ $$
