Menu Close

Question-45842

Tinku Tara 0 Comments
Pin




Question Number 45842 by gunawan last updated on 17/Oct/18
Commented by maxmathsup by imad last updated on 17/Oct/18
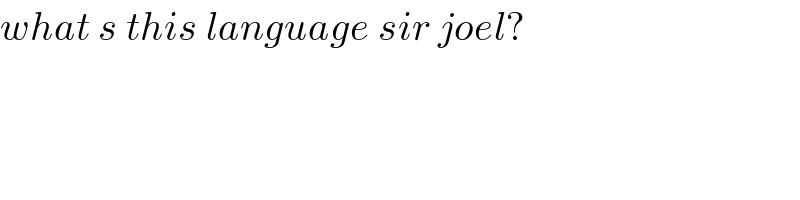
what s this language sir joel?
$${what}\:{s}\:{this}\:{language}\:{sir}\:{joel}? \\ $$
Commented by MJS last updated on 17/Oct/18
English please
$$\mathrm{English}\:\mathrm{please} \\ $$
Commented by Joel578 last updated on 17/Oct/18
It used Indonesian language
$$\mathrm{It}\:\mathrm{used}\:\mathrm{Indonesian}\:\mathrm{language} \\ $$
Commented by Joel578 last updated on 17/Oct/18
Translate: Solve the equations below: a) b) c) d) e) f) g) Hint: use the identity a cos x + b sin x = k cos (x − α)
$$\mathrm{Translate}: \\ $$$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{equations}\:\mathrm{below}: \\ $$$$\left.{a}\right) \\ $$$$\left.{b}\right) \\ $$$$\left.{c}\right) \\ $$$$\left.{d}\right) \\ $$$$\left.{e}\right) \\ $$$$\left.{f}\right) \\ $$$$\left.{g}\right) \\ $$$$\mathrm{Hint}:\:\mathrm{use}\:\mathrm{the}\:\mathrm{identity}\:\:\:{a}\:\mathrm{cos}\:{x}\:+\:{b}\:\mathrm{sin}\:{x}\:=\:{k}\:\mathrm{cos}\:\left({x}\:−\:\alpha\right) \\ $$
Commented by maxmathsup by imad last updated on 17/Oct/18
thank you..
$${thank}\:{you}.. \\ $$
Commented by maxmathsup by imad last updated on 17/Oct/18
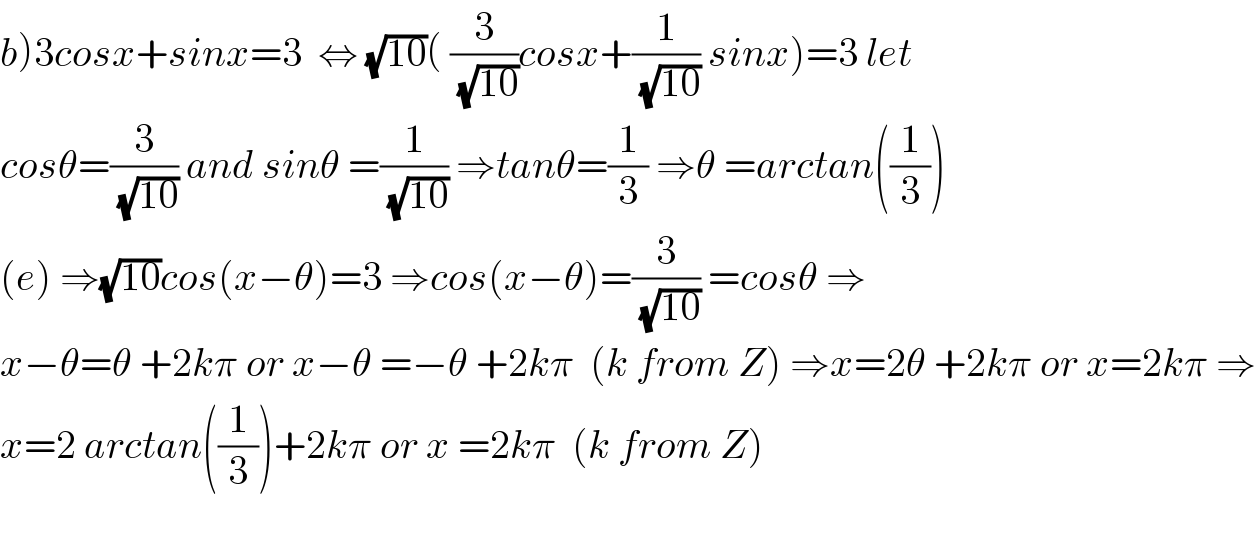
b)3cosx+sinx=3 ⇔ (√(10))( (3/( (√(10))))cosx+(1/( (√(10)))) sinx)=3 let cosθ=(3/( (√(10)))) and sinθ =(1/( (√(10)))) ⇒tanθ=(1/3) ⇒θ =arctan((1/3)) (e) ⇒(√(10))cos(x−θ)=3 ⇒cos(x−θ)=(3/( (√(10)))) =cosθ ⇒ x−θ=θ +2kπ or x−θ =−θ +2kπ (k from Z) ⇒x=2θ +2kπ or x=2kπ ⇒ x=2 arctan((1/3))+2kπ or x =2kπ (k from Z)
$$\left.{b}\right)\mathrm{3}{cosx}+{sinx}=\mathrm{3}\:\:\Leftrightarrow\:\sqrt{\mathrm{10}}\left(\:\frac{\mathrm{3}}{\:\sqrt{\mathrm{10}}}{cosx}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{10}}}\:{sinx}\right)=\mathrm{3}\:{let} \\ $$$${cos}\theta=\frac{\mathrm{3}}{\:\sqrt{\mathrm{10}}}\:{and}\:{sin}\theta\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{10}}}\:\Rightarrow{tan}\theta=\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow\theta\:={arctan}\left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$\left({e}\right)\:\Rightarrow\sqrt{\mathrm{10}}{cos}\left({x}−\theta\right)=\mathrm{3}\:\Rightarrow{cos}\left({x}−\theta\right)=\frac{\mathrm{3}}{\:\sqrt{\mathrm{10}}}\:={cos}\theta\:\Rightarrow \\ $$$${x}−\theta=\theta\:+\mathrm{2}{k}\pi\:{or}\:{x}−\theta\:=−\theta\:+\mathrm{2}{k}\pi\:\:\left({k}\:{from}\:{Z}\right)\:\Rightarrow{x}=\mathrm{2}\theta\:+\mathrm{2}{k}\pi\:{or}\:{x}=\mathrm{2}{k}\pi\:\Rightarrow \\ $$$${x}=\mathrm{2}\:{arctan}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)+\mathrm{2}{k}\pi\:{or}\:{x}\:=\mathrm{2}{k}\pi\:\:\left({k}\:{from}\:{Z}\right) \\ $$$$ \\ $$
Commented by gunawan last updated on 18/Oct/18
thank you very much sir
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{sir} \\ $$
Commented by hknkrc46 last updated on 29/Nov/18
a) cos x+(√3)sin x=1 cos x+(√3)sin x=1 cos x+tan 60sin x=1 cos x+((sin 60)/(cos 60))sin x=1 ((cos xcos 60+sin xsin 60)/(cos 60))=1 ((cos (x−60))/(cos 60))=1⇒cos (x−60)=cos 60 ⇒x−60=60 ∨ x−60=−60 ⇒x=120 ∨ x=0 b) 3cos x+sin x=3 3cos x+sin x=3⇒sin x=3−3cos x ⇒sin x=3(1−cos x) ⇒sin x(1+cos x)=3(1−cos x)(1+cos x) ⇒sin x(1+cos x)=3(1−cos^2 x) ⇒sin x(1+cos x)=3sin^2 x ⇒1+cos x=3sin x ⇒3sin x−cos x=1 (3cos x+sin x)+3(3sin x−cos x)=10sin x 3+3∙1=10sin x⇒sin x=(6/(10))=(3/5)⇒x=36,86≈37 x≈37 ∨ x≈143 c) 5cos x+4sin x=6 cos x=u ⇒ sin x=(√(1−u^2 )) 5u+4(√(1−u^2 ))=6⇒4(√(1−u^2 ))=6−5u ⇒16(1−u^2 )=(6−5u)^2 ⇒16−16u^2 =25u^2 −60u+36 ⇒41u^2 −60u+20=0 ⇒u_(1,2) =((60±(√(60^2 −4∙41∙20)))/(82))=((60±(√(320)))/(82)) ≈((60±18)/(82))⇒u_1 =cos x≈((39)/(41)) ∨ u_2 =cos x≈((21)/(41)) x≈cos^(−1) (((39)/(41))) ∨ x≈cos^(−1) (((21)/(41)))
$$\left.{a}\right)\:\mathrm{cos}\:{x}+\sqrt{\mathrm{3}}\mathrm{sin}\:{x}=\mathrm{1} \\ $$$$\mathrm{cos}\:{x}+\sqrt{\mathrm{3}}\mathrm{sin}\:{x}=\mathrm{1} \\ $$$$\mathrm{cos}\:{x}+\mathrm{tan}\:\mathrm{60sin}\:{x}=\mathrm{1} \\ $$$$\mathrm{cos}\:{x}+\frac{\mathrm{sin}\:\mathrm{60}}{\mathrm{cos}\:\mathrm{60}}\mathrm{sin}\:{x}=\mathrm{1} \\ $$$$\frac{\mathrm{cos}\:{x}\mathrm{cos}\:\mathrm{60}+\mathrm{sin}\:{x}\mathrm{sin}\:\mathrm{60}}{\mathrm{cos}\:\mathrm{60}}=\mathrm{1} \\ $$$$\frac{\mathrm{cos}\:\left({x}−\mathrm{60}\right)}{\mathrm{cos}\:\mathrm{60}}=\mathrm{1}\Rightarrow\mathrm{cos}\:\left({x}−\mathrm{60}\right)=\mathrm{cos}\:\mathrm{60} \\ $$$$\Rightarrow{x}−\mathrm{60}=\mathrm{60}\:\vee\:{x}−\mathrm{60}=−\mathrm{60} \\ $$$$\Rightarrow{x}=\mathrm{120}\:\vee\:{x}=\mathrm{0} \\ $$$$\left.{b}\right)\:\mathrm{3cos}\:{x}+\mathrm{sin}\:{x}=\mathrm{3} \\ $$$$\mathrm{3cos}\:{x}+\mathrm{sin}\:{x}=\mathrm{3}\Rightarrow\mathrm{sin}\:{x}=\mathrm{3}−\mathrm{3cos}\:{x} \\ $$$$\Rightarrow\mathrm{sin}\:{x}=\mathrm{3}\left(\mathrm{1}−\mathrm{cos}\:{x}\right) \\ $$$$\Rightarrow\mathrm{sin}\:{x}\left(\mathrm{1}+\mathrm{cos}\:{x}\right)=\mathrm{3}\left(\mathrm{1}−\mathrm{cos}\:{x}\right)\left(\mathrm{1}+\mathrm{cos}\:{x}\right) \\ $$$$\Rightarrow\mathrm{sin}\:{x}\left(\mathrm{1}+\mathrm{cos}\:{x}\right)=\mathrm{3}\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} {x}\right) \\ $$$$\Rightarrow\mathrm{sin}\:{x}\left(\mathrm{1}+\mathrm{cos}\:{x}\right)=\mathrm{3sin}\:^{\mathrm{2}} {x} \\ $$$$\Rightarrow\mathrm{1}+\mathrm{cos}\:{x}=\mathrm{3sin}\:{x} \\ $$$$\Rightarrow\mathrm{3sin}\:{x}−\mathrm{cos}\:{x}=\mathrm{1} \\ $$$$\left(\mathrm{3cos}\:{x}+\mathrm{sin}\:{x}\right)+\mathrm{3}\left(\mathrm{3sin}\:{x}−\mathrm{cos}\:{x}\right)=\mathrm{10sin}\:{x} \\ $$$$\mathrm{3}+\mathrm{3}\centerdot\mathrm{1}=\mathrm{10sin}\:{x}\Rightarrow\mathrm{sin}\:{x}=\frac{\mathrm{6}}{\mathrm{10}}=\frac{\mathrm{3}}{\mathrm{5}}\Rightarrow{x}=\mathrm{36},\mathrm{86}\approx\mathrm{37} \\ $$$${x}\approx\mathrm{37}\:\vee\:{x}\approx\mathrm{143} \\ $$$$\left.{c}\right)\:\mathrm{5cos}\:{x}+\mathrm{4sin}\:{x}=\mathrm{6} \\ $$$$\mathrm{cos}\:{x}={u}\:\Rightarrow\:\mathrm{sin}\:{x}=\sqrt{\mathrm{1}−{u}^{\mathrm{2}} } \\ $$$$\mathrm{5}{u}+\mathrm{4}\sqrt{\mathrm{1}−{u}^{\mathrm{2}} }=\mathrm{6}\Rightarrow\mathrm{4}\sqrt{\mathrm{1}−{u}^{\mathrm{2}} }=\mathrm{6}−\mathrm{5}{u} \\ $$$$\Rightarrow\mathrm{16}\left(\mathrm{1}−{u}^{\mathrm{2}} \right)=\left(\mathrm{6}−\mathrm{5}{u}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{16}−\mathrm{16}{u}^{\mathrm{2}} =\mathrm{25}{u}^{\mathrm{2}} −\mathrm{60}{u}+\mathrm{36} \\ $$$$\Rightarrow\mathrm{41}{u}^{\mathrm{2}} −\mathrm{60}{u}+\mathrm{20}=\mathrm{0} \\ $$$$\Rightarrow{u}_{\mathrm{1},\mathrm{2}} =\frac{\mathrm{60}\pm\sqrt{\mathrm{60}^{\mathrm{2}} −\mathrm{4}\centerdot\mathrm{41}\centerdot\mathrm{20}}}{\mathrm{82}}=\frac{\mathrm{60}\pm\sqrt{\mathrm{320}}}{\mathrm{82}} \\ $$$$\approx\frac{\mathrm{60}\pm\mathrm{18}}{\mathrm{82}}\Rightarrow{u}_{\mathrm{1}} =\mathrm{cos}\:{x}\approx\frac{\mathrm{39}}{\mathrm{41}}\:\vee\:{u}_{\mathrm{2}} =\mathrm{cos}\:{x}\approx\frac{\mathrm{21}}{\mathrm{41}} \\ $$$${x}\approx\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{39}}{\mathrm{41}}\right)\:\vee\:{x}\approx\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{21}}{\mathrm{41}}\right) \\ $$
Answered by Joel578 last updated on 17/Oct/18
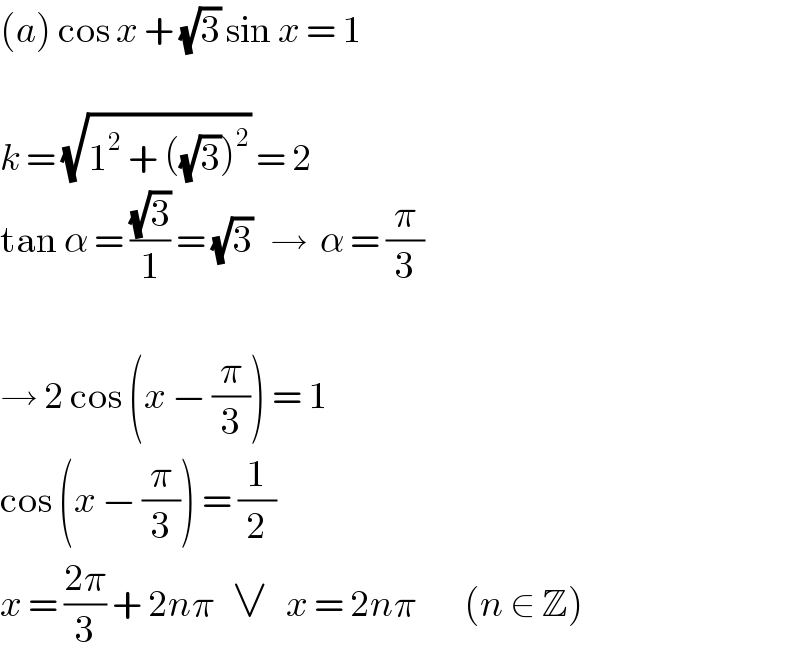
(a) cos x + (√3) sin x = 1 k = (√(1^2 + ((√3))^2 )) = 2 tan α = ((√3)/1) = (√3) → α = (π/3) → 2 cos (x − (π/3)) = 1 cos (x − (π/3)) = (1/2) x = ((2π)/3) + 2nπ ∨ x = 2nπ (n ∈ Z)
$$\left({a}\right)\:\mathrm{cos}\:{x}\:+\:\sqrt{\mathrm{3}}\:\mathrm{sin}\:{x}\:=\:\mathrm{1} \\ $$$$ \\ $$$${k}\:=\:\sqrt{\mathrm{1}^{\mathrm{2}} \:+\:\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }\:=\:\mathrm{2} \\ $$$$\mathrm{tan}\:\alpha\:=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{1}}\:=\:\sqrt{\mathrm{3}}\:\:\:\rightarrow\:\:\alpha\:=\:\frac{\pi}{\mathrm{3}} \\ $$$$ \\ $$$$\rightarrow\:\mathrm{2}\:\mathrm{cos}\:\left({x}\:−\:\frac{\pi}{\mathrm{3}}\right)\:=\:\mathrm{1} \\ $$$$\mathrm{cos}\:\left({x}\:−\:\frac{\pi}{\mathrm{3}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${x}\:=\:\frac{\mathrm{2}\pi}{\mathrm{3}}\:+\:\mathrm{2}{n}\pi\:\:\:\vee\:\:\:{x}\:=\:\mathrm{2}{n}\pi\:\:\:\:\:\:\:\:\left({n}\:\in\:\mathbb{Z}\right) \\ $$
Commented by gunawan last updated on 18/Oct/18
thanks
$$\mathrm{thanks} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *