Question Number 45930 by Tawa1 last updated on 18/Oct/18

Answered by MJS last updated on 19/Oct/18
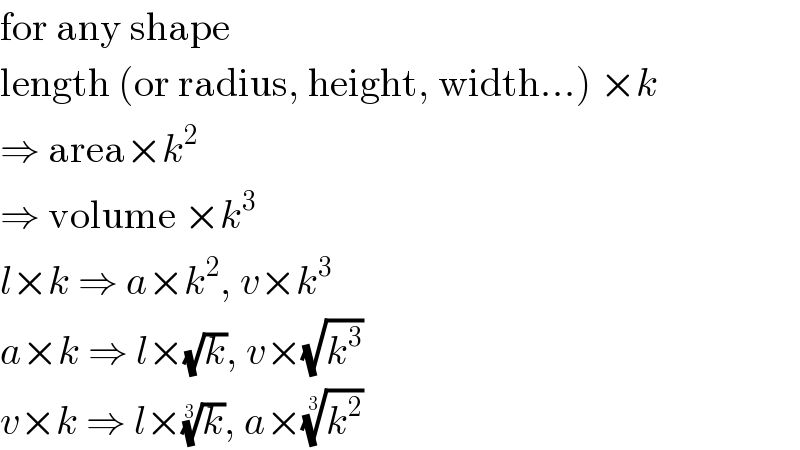
$$\mathrm{for}\:\mathrm{any}\:\mathrm{shape} \\ $$$$\mathrm{length}\:\left(\mathrm{or}\:\mathrm{radius},\:\mathrm{height},\:\mathrm{width}…\right)\:×{k} \\ $$$$\Rightarrow\:\mathrm{area}×{k}^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{volume}\:×{k}^{\mathrm{3}} \\ $$$${l}×{k}\:\Rightarrow\:{a}×{k}^{\mathrm{2}} ,\:{v}×{k}^{\mathrm{3}} \\ $$$${a}×{k}\:\Rightarrow\:{l}×\sqrt{{k}},\:{v}×\sqrt{{k}^{\mathrm{3}} } \\ $$$${v}×{k}\:\Rightarrow\:{l}×\sqrt[{\mathrm{3}}]{{k}},\:{a}×\sqrt[{\mathrm{3}}]{{k}^{\mathrm{2}} } \\ $$
Commented by Tawa1 last updated on 19/Oct/18
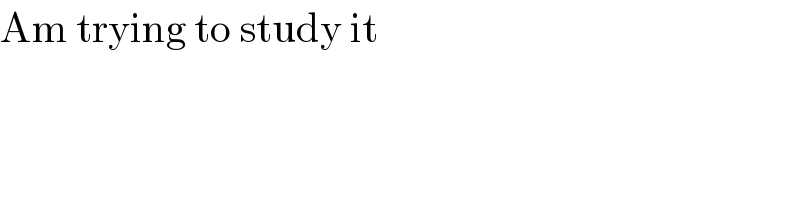
$$\mathrm{Am}\:\mathrm{trying}\:\mathrm{to}\:\mathrm{study}\:\mathrm{it} \\ $$
Commented by Tawa1 last updated on 19/Oct/18
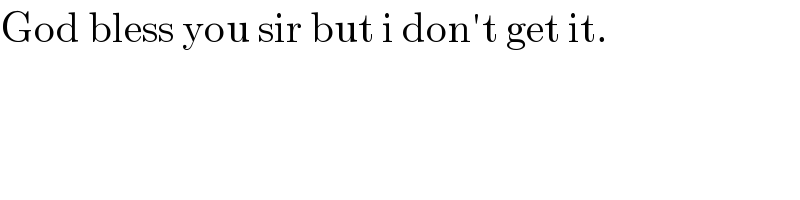
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}\:\mathrm{but}\:\mathrm{i}\:\mathrm{don}'\mathrm{t}\:\mathrm{get}\:\mathrm{it}. \\ $$
Commented by Tawa1 last updated on 19/Oct/18
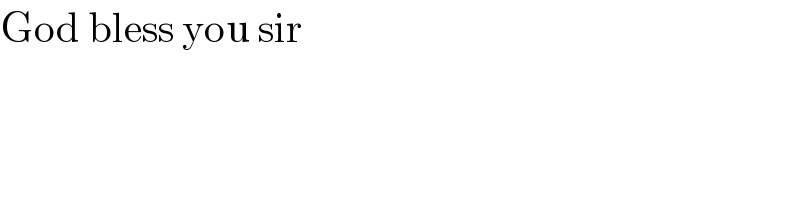
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by MJS last updated on 19/Oct/18
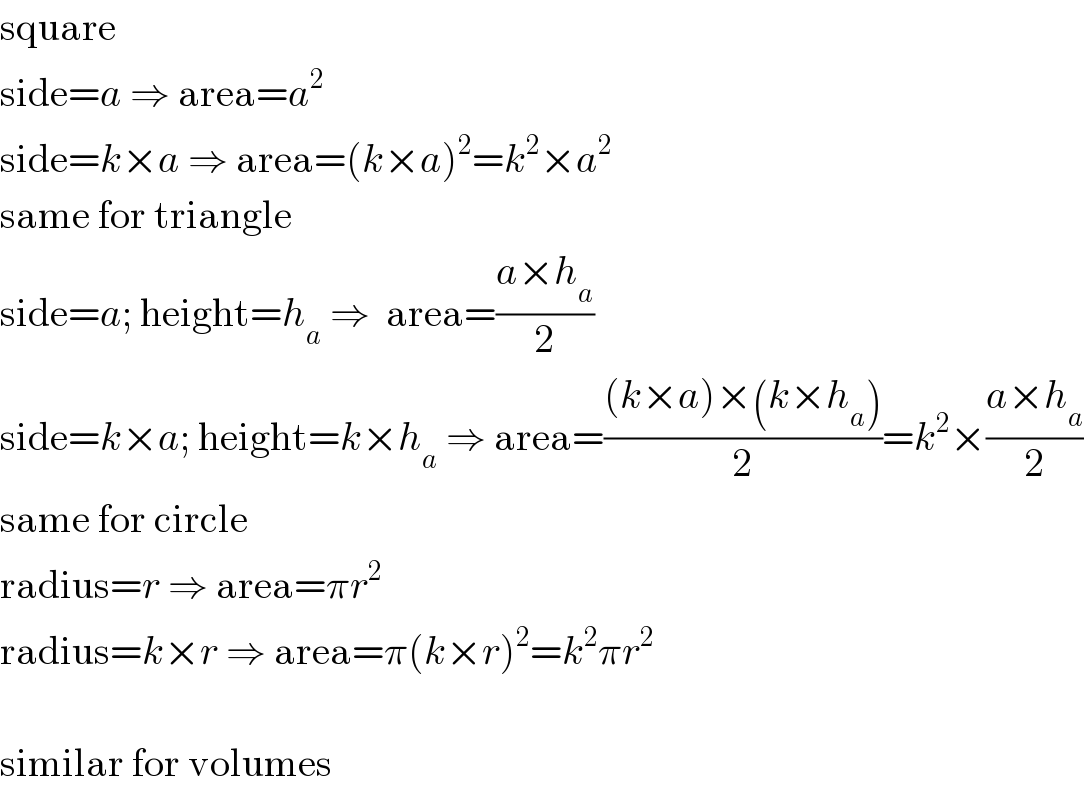
$$\mathrm{square} \\ $$$$\mathrm{side}={a}\:\Rightarrow\:\mathrm{area}={a}^{\mathrm{2}} \\ $$$$\mathrm{side}={k}×{a}\:\Rightarrow\:\mathrm{area}=\left({k}×{a}\right)^{\mathrm{2}} ={k}^{\mathrm{2}} ×{a}^{\mathrm{2}} \\ $$$$\mathrm{same}\:\mathrm{for}\:\mathrm{triangle} \\ $$$$\mathrm{side}={a};\:\mathrm{height}={h}_{{a}} \:\Rightarrow\:\:\mathrm{area}=\frac{{a}×{h}_{{a}} }{\mathrm{2}} \\ $$$$\mathrm{side}={k}×{a};\:\mathrm{height}={k}×{h}_{{a}} \:\Rightarrow\:\mathrm{area}=\frac{\left({k}×{a}\right)×\left({k}×{h}_{{a}} \right)}{\mathrm{2}}={k}^{\mathrm{2}} ×\frac{{a}×{h}_{{a}} }{\mathrm{2}} \\ $$$$\mathrm{same}\:\mathrm{for}\:\mathrm{circle} \\ $$$$\mathrm{radius}={r}\:\Rightarrow\:\mathrm{area}=\pi{r}^{\mathrm{2}} \\ $$$$\mathrm{radius}={k}×{r}\:\Rightarrow\:\mathrm{area}=\pi\left({k}×{r}\right)^{\mathrm{2}} ={k}^{\mathrm{2}} \pi{r}^{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{similar}\:\mathrm{for}\:\mathrm{volumes} \\ $$
