Menu Close

Question-46020

Tinku Tara 0 Comments
Pin




Question Number 46020 by mondodotto@gmail.com last updated on 20/Oct/18
Answered by tanmay.chaudhury50@gmail.com last updated on 20/Oct/18
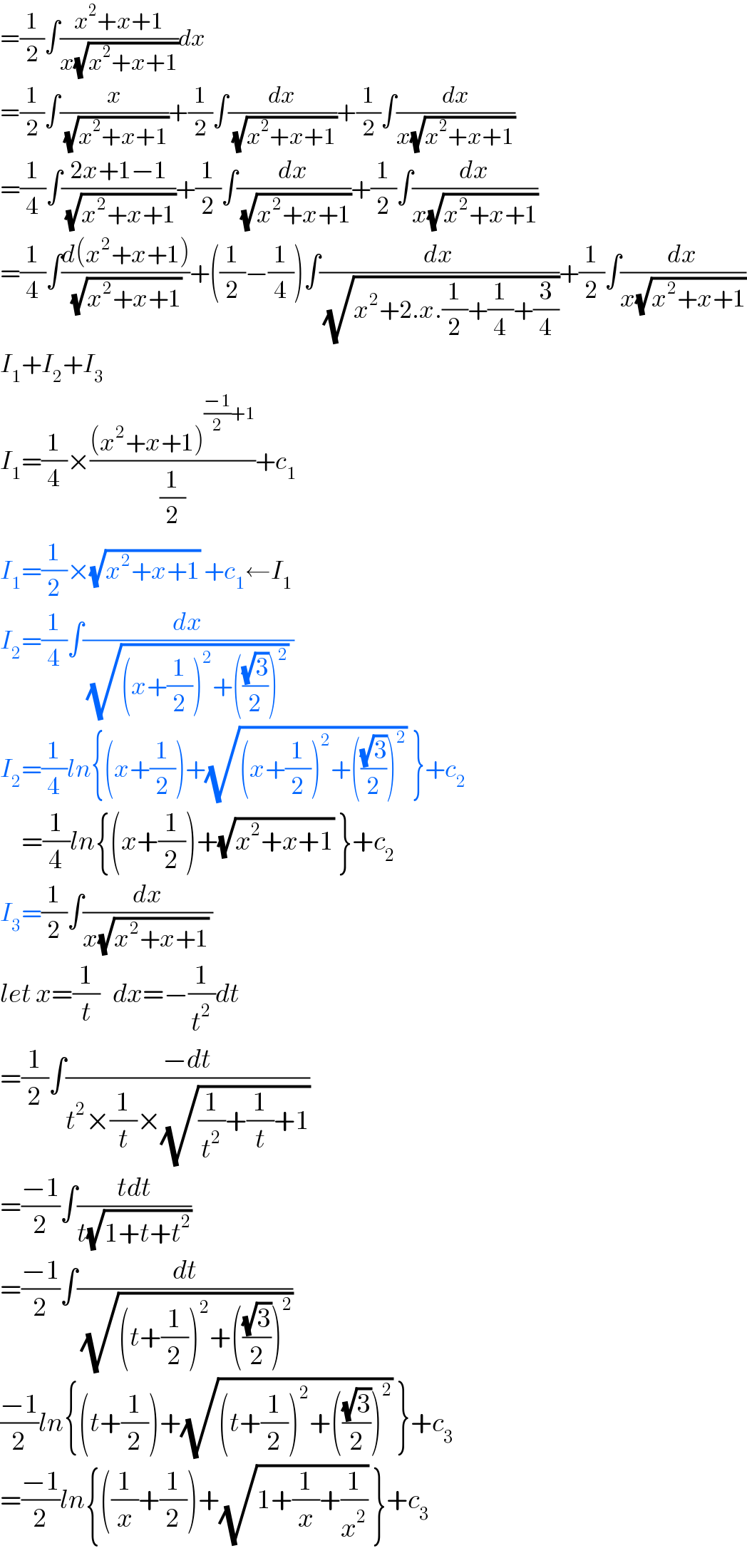
=(1/2)∫((x^2 +x+1)/(x(√(x^2 +x+1))))dx =(1/2)∫(x/( (√(x^2 +x+1))))+(1/2)∫(dx/( (√(x^2 +x+1))))+(1/2)∫(dx/(x(√(x^2 +x+1)))) =(1/4)∫((2x+1−1)/( (√(x^2 +x+1))))+(1/2)∫(dx/( (√(x^2 +x+1))))+(1/2)∫(dx/(x(√(x^2 +x+1)))) =(1/4)∫((d(x^2 +x+1))/( (√(x^2 +x+1))))+((1/2)−(1/4))∫(dx/( (√(x^2 +2.x.(1/2)+(1/4)+(3/4)))))+(1/2)∫(dx/(x(√(x^2 +x+1)))) I_1 +I_2 +I_3 I_1 =(1/4)×(((x^2 +x+1)^(((−1)/2)+1) )/(1/2))+c_1 I_1 =(1/2)×(√(x^2 +x+1)) +c_1 ←I_1 I_2 =(1/4)∫(dx/( (√((x+(1/2))^2 +(((√3)/2))^2 )) )) I_2 =(1/4)ln{(x+(1/2))+(√((x+(1/2))^2 +(((√3)/2))^2 )) }+c_2 =(1/4)ln{(x+(1/2))+(√(x^2 +x+1)) }+c_2 I_3 =(1/2)∫(dx/(x(√(x^2 +x+1)) )) let x=(1/t) dx=−(1/t^2 )dt =(1/2)∫((−dt)/(t^2 ×(1/t)×(√((1/t^2 )+(1/t)+1)))) =((−1)/2)∫((tdt)/(t(√(1+t+t^2 )))) =((−1)/2)∫(dt/( (√((t+(1/2))^2 +(((√3)/2))^2 )))) ((−1)/2)ln{(t+(1/2))+(√((t+(1/2))^2 +(((√3)/2))^2 )) }+c_3 =((−1)/2)ln{((1/x)+(1/2))+(√(1+(1/x)+(1/x^2 ))) }+c_3
$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{{x}\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{{x}\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{2}{x}+\mathrm{1}−\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{{x}\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{d}\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)}{\:\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}+\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}\right)\int\frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{2}.{x}.\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{4}}}}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{{x}\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}} \\ $$$${I}_{\mathrm{1}} +{I}_{\mathrm{2}} +{I}_{\mathrm{3}} \\ $$$${I}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{4}}×\frac{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\frac{−\mathrm{1}}{\mathrm{2}}+\mathrm{1}} }{\frac{\mathrm{1}}{\mathrm{2}}}+{c}_{\mathrm{1}} \\ $$$${I}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}×\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\:+{c}_{\mathrm{1}} \leftarrow{I}_{\mathrm{1}} \\ $$$${I}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{dx}}{\:\sqrt{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }\:} \\ $$$${I}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}{ln}\left\{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)+\sqrt{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }\:\right\}+{c}_{\mathrm{2}} \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}{ln}\left\{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)+\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\:\right\}+{c}_{\mathrm{2}} \\ $$$${I}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{{x}\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\:} \\ $$$${let}\:{x}=\frac{\mathrm{1}}{{t}}\:\:\:{dx}=−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{−{dt}}{{t}^{\mathrm{2}} ×\frac{\mathrm{1}}{{t}}×\sqrt{\frac{\mathrm{1}}{{t}^{\mathrm{2}} }+\frac{\mathrm{1}}{{t}}+\mathrm{1}}} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{2}}\int\frac{{tdt}}{{t}\sqrt{\mathrm{1}+{t}+{t}^{\mathrm{2}} }} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{\:\sqrt{\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }} \\ $$$$\frac{−\mathrm{1}}{\mathrm{2}}{ln}\left\{\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)+\sqrt{\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }\:\right\}+{c}_{\mathrm{3}} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{2}}{ln}\left\{\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{\mathrm{2}}\right)+\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}\:\right\}+{c}_{\mathrm{3}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *