Question Number 46156 by Meritguide1234 last updated on 21/Oct/18
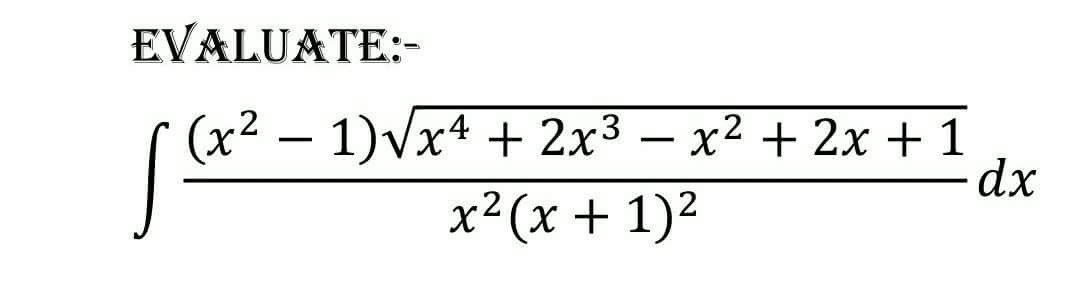
Answered by tanmay.chaudhury50@gmail.com last updated on 21/Oct/18
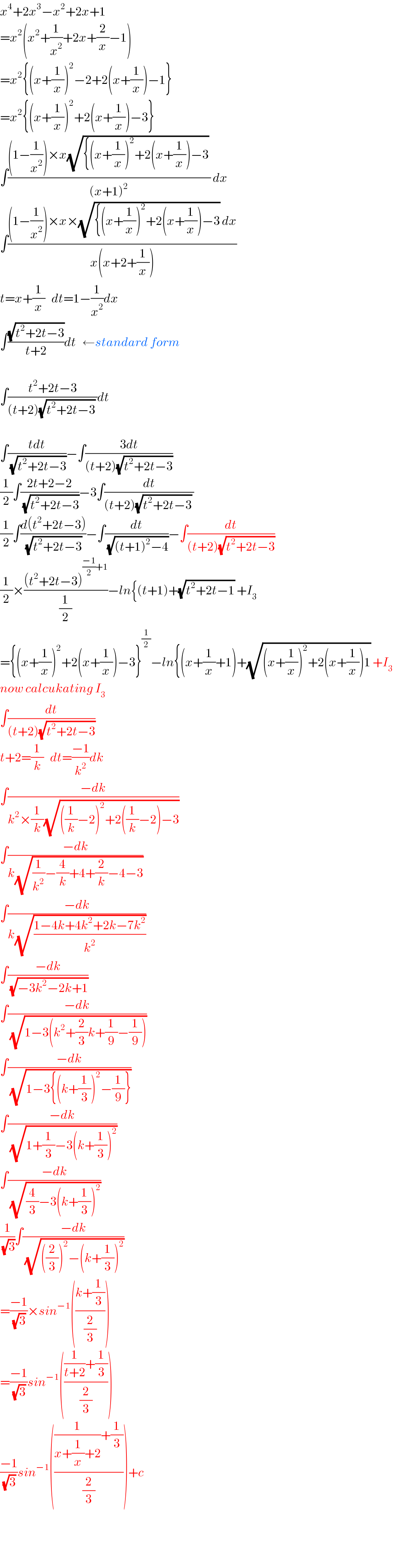
$${x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} −{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1} \\ $$$$={x}^{\mathrm{2}} \left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{2}{x}+\frac{\mathrm{2}}{{x}}−\mathrm{1}\right) \\ $$$$={x}^{\mathrm{2}} \left\{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{2}+\mathrm{2}\left({x}+\frac{\mathrm{1}}{{x}}\right)−\mathrm{1}\right\} \\ $$$$={x}^{\mathrm{2}} \left\{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{2}\left({x}+\frac{\mathrm{1}}{{x}}\right)−\mathrm{3}\right\} \\ $$$$\int\frac{\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)×{x}\sqrt{\left\{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{2}\left({x}+\frac{\mathrm{1}}{{x}}\right)−\mathrm{3}\right.}\:}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }\:{dx} \\ $$$$\int\frac{\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)×{x}×\sqrt{\left\{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{2}\left({x}+\frac{\mathrm{1}}{{x}}\right)−\mathrm{3}\right.}\:{dx}}{{x}\left({x}+\mathrm{2}+\frac{\mathrm{1}}{{x}}\right)} \\ $$$${t}={x}+\frac{\mathrm{1}}{{x}}\:\:\:{dt}=\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{dx} \\ $$$$\int\frac{\sqrt{{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{3}}}{{t}+\mathrm{2}}{dt}\:\:\:\leftarrow{standard}\:{form}\: \\ $$$$ \\ $$$$\int\frac{{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{3}}{\left({t}+\mathrm{2}\right)\sqrt{{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{3}}\:}{dt} \\ $$$$ \\ $$$$\int\frac{{tdt}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{3}}}−\int\frac{\mathrm{3}{dt}}{\left({t}+\mathrm{2}\right)\sqrt{{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{3}}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{t}+\mathrm{2}−\mathrm{2}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{3}}}−\mathrm{3}\int\frac{{dt}}{\left({t}+\mathrm{2}\right)\sqrt{{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{3}}\:} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{3}\right)}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{3}}}−\int\frac{{dt}}{\:\sqrt{\left({t}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}}}−\int\frac{{dt}}{\left({t}+\mathrm{2}\right)\sqrt{{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{3}}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\frac{\left({t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{3}\right)^{\frac{−\mathrm{1}}{\mathrm{2}}+\mathrm{1}} }{\frac{\mathrm{1}}{\mathrm{2}}}−{ln}\left\{\left({t}+\mathrm{1}\right)+\sqrt{{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{1}}\:+{I}_{\mathrm{3}} \right. \\ $$$$=\left\{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{2}\left({x}+\frac{\mathrm{1}}{{x}}\right)−\mathrm{3}\right\}^{\frac{\mathrm{1}}{\mathrm{2}}} −{ln}\left\{\left({x}+\frac{\mathrm{1}}{{x}}+\mathrm{1}\right)+\sqrt{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{2}\left({x}+\frac{\mathrm{1}}{{x}}\right)\mathrm{1}}\:+{I}_{\mathrm{3}} \right. \\ $$$${now}\:{calcukating}\:{I}_{\mathrm{3}} \\ $$$$\int\frac{{dt}}{\left({t}+\mathrm{2}\right)\sqrt{{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{3}}} \\ $$$${t}+\mathrm{2}=\frac{\mathrm{1}}{{k}}\:\:\:{dt}=\frac{−\mathrm{1}}{{k}^{\mathrm{2}} }{dk} \\ $$$$\int\frac{−{dk}}{{k}^{\mathrm{2}} ×\frac{\mathrm{1}}{{k}}\sqrt{\left(\frac{\mathrm{1}}{{k}}−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{2}\left(\frac{\mathrm{1}}{{k}}−\mathrm{2}\right)−\mathrm{3}}} \\ $$$$\int\frac{−{dk}}{{k}\sqrt{\frac{\mathrm{1}}{{k}^{\mathrm{2}} }−\frac{\mathrm{4}}{{k}}+\mathrm{4}+\frac{\mathrm{2}}{{k}}−\mathrm{4}−\mathrm{3}}} \\ $$$$\int\frac{−{dk}}{{k}\sqrt{\frac{\mathrm{1}−\mathrm{4}{k}+\mathrm{4}{k}^{\mathrm{2}} +\mathrm{2}{k}−\mathrm{7}{k}^{\mathrm{2}} }{{k}^{\mathrm{2}} }}} \\ $$$$\int\frac{−{dk}}{\:\sqrt{−\mathrm{3}{k}^{\mathrm{2}} −\mathrm{2}{k}+\mathrm{1}}} \\ $$$$\int\frac{−{dk}}{\:\sqrt{\mathrm{1}−\mathrm{3}\left({k}^{\mathrm{2}} +\frac{\mathrm{2}}{\mathrm{3}}{k}+\frac{\mathrm{1}}{\mathrm{9}}−\frac{\mathrm{1}}{\mathrm{9}}\right)}} \\ $$$$\int\frac{−{dk}}{\:\sqrt{\mathrm{1}−\mathrm{3}\left\{\left({k}+\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{9}}\right\}}} \\ $$$$\int\frac{−{dk}}{\:\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{3}\left({k}+\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} }} \\ $$$$\int\frac{−{dk}}{\:\sqrt{\frac{\mathrm{4}}{\mathrm{3}}−\mathrm{3}\left({k}+\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} }} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\int\frac{−{dk}}{\:\sqrt{\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{2}} −\left({k}+\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} }} \\ $$$$=\frac{−\mathrm{1}}{\:\sqrt{\mathrm{3}}}×{sin}^{−\mathrm{1}} \left(\frac{{k}+\frac{\mathrm{1}}{\mathrm{3}}}{\frac{\mathrm{2}}{\mathrm{3}}}\right) \\ $$$$=\frac{−\mathrm{1}}{\:\sqrt{\mathrm{3}}}{sin}^{−\mathrm{1}} \left(\frac{\frac{\mathrm{1}}{{t}+\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}}{\frac{\mathrm{2}}{\mathrm{3}}}\right) \\ $$$$\frac{−\mathrm{1}}{\:\sqrt{\mathrm{3}}}{sin}^{−\mathrm{1}} \left(\frac{\frac{\mathrm{1}}{{x}+\frac{\mathrm{1}}{{x}}+\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}}{\frac{\mathrm{2}}{\mathrm{3}}}\right)+{c} \\ $$$$ \\ $$$$ \\ $$
Commented by Meritguide1234 last updated on 22/Oct/18

$${very}\:{nice} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 22/Oct/18

$${thank}\:{you}\:{sir}\:… \\ $$
