Question Number 46168 by peter frank last updated on 21/Oct/18
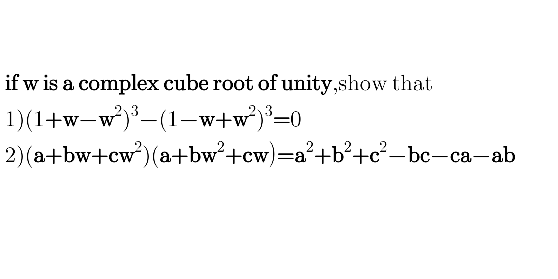
Answered by tanmay.chaudhury50@gmail.com last updated on 22/Oct/18
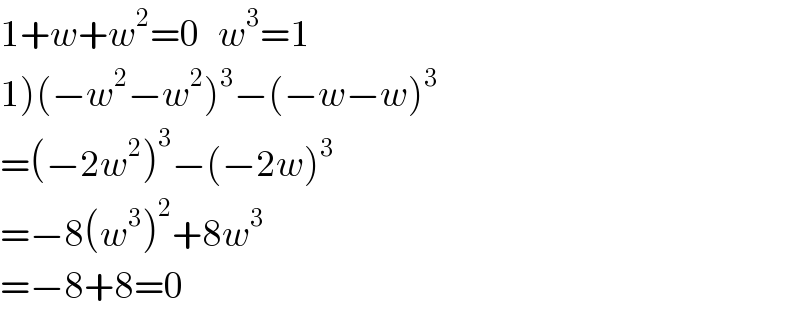
$$\mathrm{1}+{w}+{w}^{\mathrm{2}} =\mathrm{0}\:\:\:{w}^{\mathrm{3}} =\mathrm{1} \\ $$$$\left.\mathrm{1}\right)\left(−{w}^{\mathrm{2}} −{w}^{\mathrm{2}} \right)^{\mathrm{3}} −\left(−{w}−{w}\right)^{\mathrm{3}} \\ $$$$=\left(−\mathrm{2}{w}^{\mathrm{2}} \right)^{\mathrm{3}} −\left(−\mathrm{2}{w}\right)^{\mathrm{3}} \\ $$$$=−\mathrm{8}\left({w}^{\mathrm{3}} \right)^{\mathrm{2}} +\mathrm{8}{w}^{\mathrm{3}} \\ $$$$=−\mathrm{8}+\mathrm{8}=\mathrm{0} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 22/Oct/18
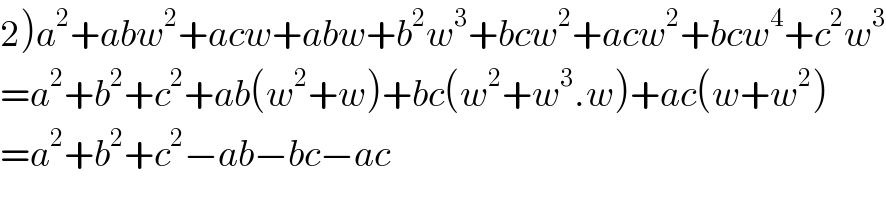
$$\left.\mathrm{2}\right){a}^{\mathrm{2}} +{abw}^{\mathrm{2}} +{acw}+{abw}+{b}^{\mathrm{2}} {w}^{\mathrm{3}} +{bcw}^{\mathrm{2}} +{acw}^{\mathrm{2}} +{bcw}^{\mathrm{4}} +{c}^{\mathrm{2}} {w}^{\mathrm{3}} \\ $$$$={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{ab}\left({w}^{\mathrm{2}} +{w}\right)+{bc}\left({w}^{\mathrm{2}} +{w}^{\mathrm{3}} .{w}\right)+{ac}\left({w}+{w}^{\mathrm{2}} \right) \\ $$$$={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{ab}−{bc}−{ac} \\ $$
