Question-46277

Question Number 46277 by rahul 19 last updated on 23/Oct/18

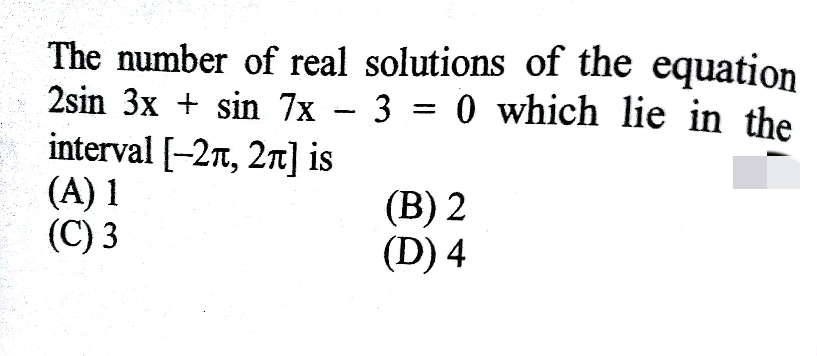
Commented by rahul 19 last updated on 23/Oct/18

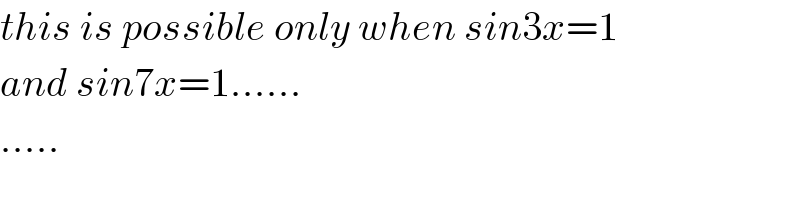
this is possible only when sin3x=1 and sin7x=1...... .....

$${this}\:{is}\:{possible}\:{only}\:{when}\:{sin}\mathrm{3}{x}=\mathrm{1} \\ $$$${and}\:{sin}\mathrm{7}{x}=\mathrm{1}…… \\ $$$$….. \\ $$

Commented by MJS last updated on 23/Oct/18

yes! you already found the solution, all you need is to calculate it

$$\mathrm{yes}!\:\mathrm{you}\:\mathrm{already}\:\mathrm{found}\:\mathrm{the}\:\mathrm{solution},\:\mathrm{all}\:\mathrm{you} \\ $$$$\mathrm{need}\:\mathrm{is}\:\mathrm{to}\:\mathrm{calculate}\:\mathrm{it} \\ $$

Answered by MJS last updated on 27/Oct/18

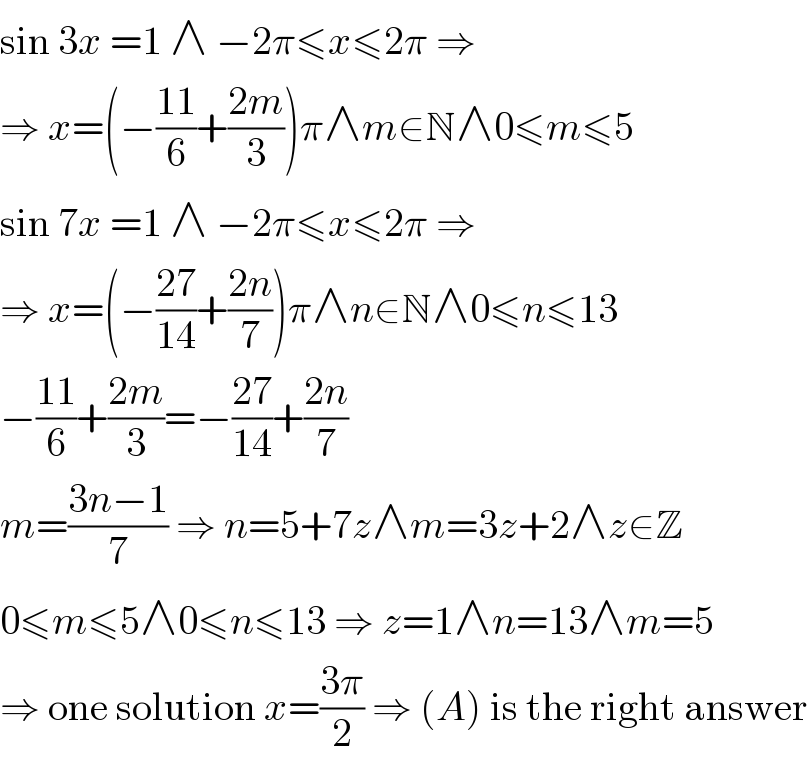
sin 3x =1 ∧ −2π≤x≤2π ⇒ ⇒ x=(−((11)/6)+((2m)/3))π∧m∈N∧0≤m≤5 sin 7x =1 ∧ −2π≤x≤2π ⇒ ⇒ x=(−((27)/(14))+((2n)/7))π∧n∈N∧0≤n≤13 −((11)/6)+((2m)/3)=−((27)/(14))+((2n)/7) m=((3n−1)/7) ⇒ n=5+7z∧m=3z+2∧z∈Z 0≤m≤5∧0≤n≤13 ⇒ z=1∧n=13∧m=5 ⇒ one solution x=((3π)/2) ⇒ (A) is the right answer

$$\mathrm{sin}\:\mathrm{3}{x}\:=\mathrm{1}\:\wedge\:−\mathrm{2}\pi\leqslant{x}\leqslant\mathrm{2}\pi\:\Rightarrow \\ $$$$\Rightarrow\:{x}=\left(−\frac{\mathrm{11}}{\mathrm{6}}+\frac{\mathrm{2}{m}}{\mathrm{3}}\right)\pi\wedge{m}\in\mathbb{N}\wedge\mathrm{0}\leqslant{m}\leqslant\mathrm{5} \\ $$$$\mathrm{sin}\:\mathrm{7}{x}\:=\mathrm{1}\:\wedge\:−\mathrm{2}\pi\leqslant{x}\leqslant\mathrm{2}\pi\:\Rightarrow \\ $$$$\Rightarrow\:{x}=\left(−\frac{\mathrm{27}}{\mathrm{14}}+\frac{\mathrm{2}{n}}{\mathrm{7}}\right)\pi\wedge{n}\in\mathbb{N}\wedge\mathrm{0}\leqslant{n}\leqslant\mathrm{13} \\ $$$$−\frac{\mathrm{11}}{\mathrm{6}}+\frac{\mathrm{2}{m}}{\mathrm{3}}=−\frac{\mathrm{27}}{\mathrm{14}}+\frac{\mathrm{2}{n}}{\mathrm{7}} \\ $$$${m}=\frac{\mathrm{3}{n}−\mathrm{1}}{\mathrm{7}}\:\Rightarrow\:{n}=\mathrm{5}+\mathrm{7}{z}\wedge{m}=\mathrm{3}{z}+\mathrm{2}\wedge{z}\in\mathbb{Z} \\ $$$$\mathrm{0}\leqslant{m}\leqslant\mathrm{5}\wedge\mathrm{0}\leqslant{n}\leqslant\mathrm{13}\:\Rightarrow\:{z}=\mathrm{1}\wedge{n}=\mathrm{13}\wedge{m}=\mathrm{5} \\ $$$$\Rightarrow\:\mathrm{one}\:\mathrm{solution}\:{x}=\frac{\mathrm{3}\pi}{\mathrm{2}}\:\Rightarrow\:\left({A}\right)\:\mathrm{is}\:\mathrm{the}\:\mathrm{right}\:\mathrm{answer} \\ $$

Commented by rahul 19 last updated on 24/Oct/18

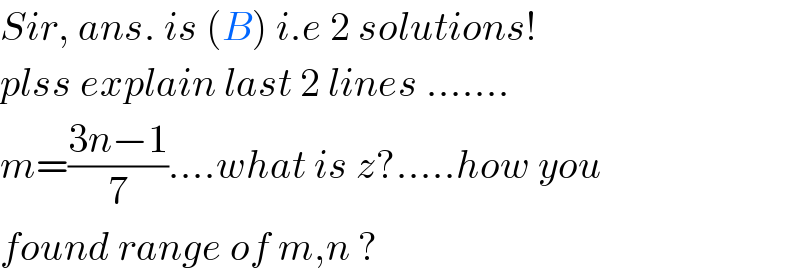
Sir, ans. is (B) i.e 2 solutions! plss explain last 2 lines ....... m=((3n−1)/7)....what is z?.....how you found range of m,n ?

$${Sir},\:{ans}.\:{is}\:\left({B}\right)\:{i}.{e}\:\mathrm{2}\:{solutions}! \\ $$$${plss}\:{explain}\:{last}\:\mathrm{2}\:{lines}\:……. \\ $$$${m}=\frac{\mathrm{3}{n}−\mathrm{1}}{\mathrm{7}}….{what}\:{is}\:{z}?…..{how}\:{you} \\ $$$${found}\:{range}\:{of}\:{m},{n}\:? \\ $$

Commented by MJS last updated on 24/Oct/18

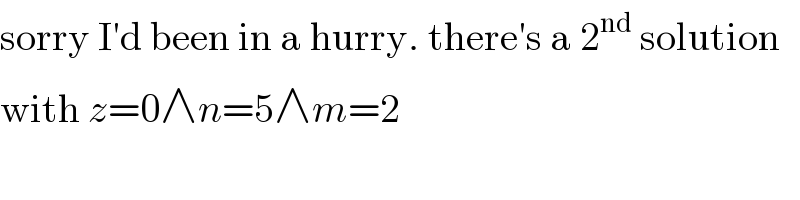
sorry I′d been in a hurry. there′s a 2^(nd) solution with z=0∧n=5∧m=2

$$\mathrm{sorry}\:\mathrm{I}'\mathrm{d}\:\mathrm{been}\:\mathrm{in}\:\mathrm{a}\:\mathrm{hurry}.\:\mathrm{there}'\mathrm{s}\:\mathrm{a}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{solution} \\ $$$$\mathrm{with}\:{z}=\mathrm{0}\wedge{n}=\mathrm{5}\wedge{m}=\mathrm{2} \\ $$

Commented by MJS last updated on 24/Oct/18

range of m, n is clear because of the given borders [−2π; 2π] m=((3n−1)/7)∧m∈Z⇒((3n−1)/7)∈Z⇒7∣(3n−1)⇒n∈{...; −9; −2; 5; 12; 19; ...}⇒n=5+7z

$$\mathrm{range}\:\mathrm{of}\:{m},\:{n}\:\mathrm{is}\:\mathrm{clear}\:\mathrm{because}\:\mathrm{of}\:\mathrm{the}\:\mathrm{given} \\ $$$$\mathrm{borders}\:\left[−\mathrm{2}\pi;\:\mathrm{2}\pi\right] \\ $$$${m}=\frac{\mathrm{3}{n}−\mathrm{1}}{\mathrm{7}}\wedge{m}\in\mathbb{Z}\Rightarrow\frac{\mathrm{3}{n}−\mathrm{1}}{\mathrm{7}}\in\mathbb{Z}\Rightarrow\mathrm{7}\mid\left(\mathrm{3}{n}−\mathrm{1}\right)\Rightarrow{n}\in\left\{…;\:−\mathrm{9};\:−\mathrm{2};\:\mathrm{5};\:\mathrm{12};\:\mathrm{19};\:…\right\}\Rightarrow{n}=\mathrm{5}+\mathrm{7}{z} \\ $$

Commented by rahul 19 last updated on 27/Oct/18

$${Here}\:{we}\:{are}\:{using}\:{hit}\:{and}\:{trial}\:{method}, \\ $$$${right}?\:{So}\:{how}\:{will}\:{you}\:{prove}\:{no}\:{other} \\ $$$${solution}\:{exists}\:{except}\:{these}\:{two}….?? \\ $$

Commented by MJS last updated on 27/Oct/18

not hit and trial. we know −2≤2sin 3x ≤2 and −1≤sin x ≤1. we need sin 3x =1∧sin 7x =1 I generally solved both equations and looked for which values of m and n the value of x is in the demanded interval [−2π; 2π]. then I needed to find those values of x for which both equations are true. I can′t see any other path...

$$\mathrm{not}\:\mathrm{hit}\:\mathrm{and}\:\mathrm{trial}.\:\mathrm{we}\:\mathrm{know}\:−\mathrm{2}\leqslant\mathrm{2sin}\:\mathrm{3}{x}\:\leqslant\mathrm{2}\:\mathrm{and} \\ $$$$−\mathrm{1}\leqslant\mathrm{sin}\:{x}\:\leqslant\mathrm{1}.\:\mathrm{we}\:\mathrm{need}\:\mathrm{sin}\:\mathrm{3}{x}\:=\mathrm{1}\wedge\mathrm{sin}\:\mathrm{7}{x}\:=\mathrm{1} \\ $$$$\mathrm{I}\:\mathrm{generally}\:\mathrm{solved}\:\mathrm{both}\:\mathrm{equations}\:\mathrm{and}\:\mathrm{looked} \\ $$$$\mathrm{for}\:\mathrm{which}\:\mathrm{values}\:\mathrm{of}\:{m}\:\mathrm{and}\:{n}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{x}\:\mathrm{is} \\ $$$$\mathrm{in}\:\mathrm{the}\:\mathrm{demanded}\:\mathrm{interval}\:\left[−\mathrm{2}\pi;\:\mathrm{2}\pi\right].\:\mathrm{then}\:\mathrm{I} \\ $$$$\mathrm{needed}\:\mathrm{to}\:\mathrm{find}\:\mathrm{those}\:\mathrm{values}\:\mathrm{of}\:{x}\:\mathrm{for}\:\mathrm{which} \\ $$$$\mathrm{both}\:\mathrm{equations}\:\mathrm{are}\:\mathrm{true}.\:\mathrm{I}\:\mathrm{can}'\mathrm{t}\:\mathrm{see}\:\mathrm{any}\:\mathrm{other} \\ $$$$\mathrm{path}… \\ $$

Commented by MJS last updated on 27/Oct/18

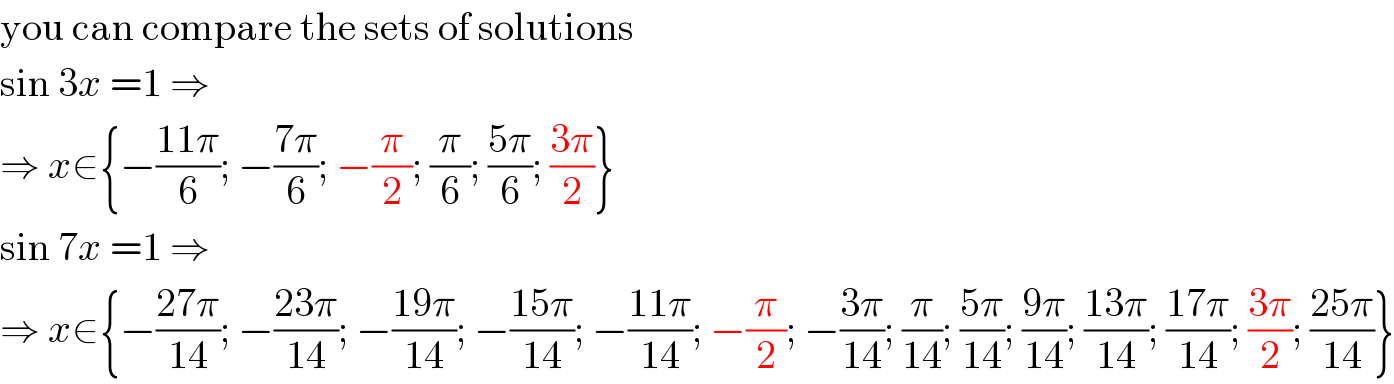
you can compare the sets of solutions sin 3x =1 ⇒ ⇒ x∈{−((11π)/6); −((7π)/6); −(π/2); (π/6); ((5π)/6); ((3π)/2)} sin 7x =1 ⇒ ⇒ x∈{−((27π)/(14)); −((23π)/(14)); −((19π)/(14)); −((15π)/(14)); −((11π)/(14)); −(π/2); −((3π)/(14)); (π/(14)); ((5π)/(14)); ((9π)/(14)); ((13π)/(14)); ((17π)/(14)); ((3π)/2); ((25π)/(14))}

$$\mathrm{you}\:\mathrm{can}\:\mathrm{compare}\:\mathrm{the}\:\mathrm{sets}\:\mathrm{of}\:\mathrm{solutions} \\ $$$$\mathrm{sin}\:\mathrm{3}{x}\:=\mathrm{1}\:\Rightarrow \\ $$$$\Rightarrow\:{x}\in\left\{−\frac{\mathrm{11}\pi}{\mathrm{6}};\:−\frac{\mathrm{7}\pi}{\mathrm{6}};\:−\frac{\pi}{\mathrm{2}};\:\frac{\pi}{\mathrm{6}};\:\frac{\mathrm{5}\pi}{\mathrm{6}};\:\frac{\mathrm{3}\pi}{\mathrm{2}}\right\} \\ $$$$\mathrm{sin}\:\mathrm{7}{x}\:=\mathrm{1}\:\Rightarrow \\ $$$$\Rightarrow\:{x}\in\left\{−\frac{\mathrm{27}\pi}{\mathrm{14}};\:−\frac{\mathrm{23}\pi}{\mathrm{14}};\:−\frac{\mathrm{19}\pi}{\mathrm{14}};\:−\frac{\mathrm{15}\pi}{\mathrm{14}};\:−\frac{\mathrm{11}\pi}{\mathrm{14}};\:−\frac{\pi}{\mathrm{2}};\:−\frac{\mathrm{3}\pi}{\mathrm{14}};\:\frac{\pi}{\mathrm{14}};\:\frac{\mathrm{5}\pi}{\mathrm{14}};\:\frac{\mathrm{9}\pi}{\mathrm{14}};\:\frac{\mathrm{13}\pi}{\mathrm{14}};\:\frac{\mathrm{17}\pi}{\mathrm{14}};\:\frac{\mathrm{3}\pi}{\mathrm{2}};\:\frac{\mathrm{25}\pi}{\mathrm{14}}\right\} \\ $$

Commented by rahul 19 last updated on 28/Oct/18

thank you so much sir !��

Facebook Tweet Pin

Leave a Reply Cancel reply