Question Number 46944 by Tawa1 last updated on 02/Nov/18
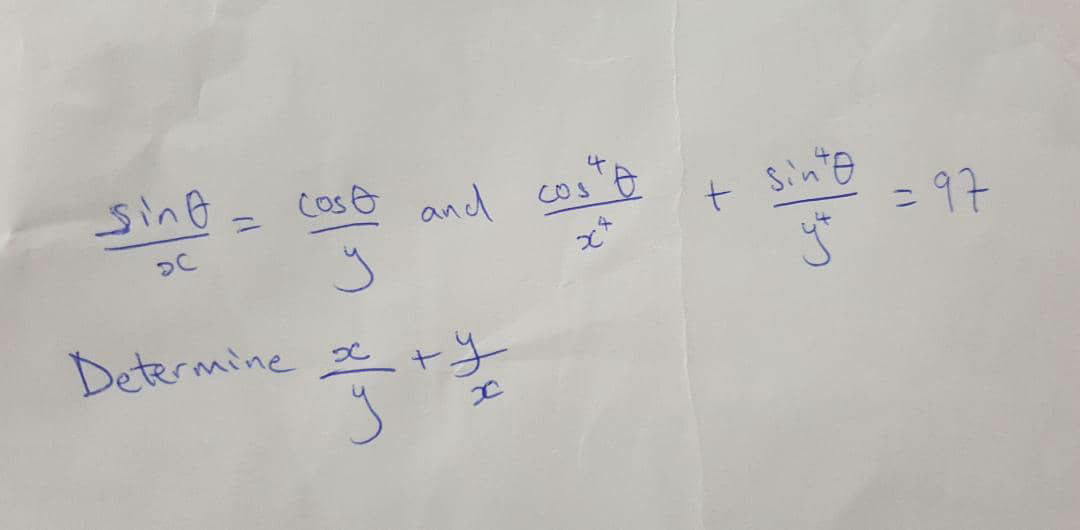
Commented by maxmathsup by imad last updated on 03/Nov/18

$${we}\:{have}\:\frac{{x}}{{y}}\:+\frac{{y}}{{x}}\:=\frac{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }{{xy}}\:\:{and} \\ $$$$\frac{{x}}{{sin}\theta}\:=\frac{{y}}{{cos}\theta}\:\Rightarrow\frac{{x}^{\mathrm{4}} }{{sin}^{\mathrm{4}} \theta}\:=\frac{{y}^{\mathrm{4}} }{{cos}^{\mathrm{4}} \theta}\:\left(×\frac{\mathrm{1}}{{x}^{\mathrm{4}} {y}^{\mathrm{4}} }\right)\Rightarrow\frac{\mathrm{1}}{{y}^{\mathrm{4}} {sin}^{\mathrm{4}} \theta}\:=\frac{\mathrm{1}}{{x}^{\mathrm{4}} {cos}^{\mathrm{4}} }\:=\frac{\mathrm{2}}{{x}^{\mathrm{4}} {cos}^{\mathrm{4}} \theta+{y}^{\mathrm{4}} {sin}^{\mathrm{4}} \theta} \\ $$$${so}\:{if}\:{we}\:{take}\:{the}\:{cond}.\:\:\frac{{sin}^{\mathrm{4}} \theta}{{x}^{\mathrm{4}} }\:+\frac{{cos}^{\mathrm{4}} \theta}{{y}^{\mathrm{4}} }\:=\mathrm{97}\:\Rightarrow\frac{{y}^{\mathrm{4}} {sin}^{\mathrm{4}} \theta\:+{x}^{\mathrm{4}} {cos}^{\mathrm{4}} \theta}{{x}^{\mathrm{4}} {y}^{\mathrm{4}} }\:=\mathrm{97}\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{{y}^{\mathrm{4}} {sin}^{\mathrm{4}} \theta}\:=\frac{\mathrm{2}}{\mathrm{97}{x}^{\mathrm{4}} {y}^{\mathrm{4}} }\:\Rightarrow\frac{\mathrm{1}}{{sin}^{\mathrm{4}} \theta}\:=\frac{\mathrm{2}}{\mathrm{97}\:{y}^{\mathrm{4}} }\:\Rightarrow\mathrm{97}\:{y}^{\mathrm{4}} \:=\mathrm{2}{sin}^{\mathrm{4}} \theta\:{also}\:{we}\:{get}\mathrm{97}{x}^{\mathrm{4}} \:=\mathrm{2}\:{cos}^{\mathrm{4}} \theta\Rightarrow \\ $$$$\mathrm{97}\left({x}^{\mathrm{4}} \:+{y}^{\mathrm{4}} \right)=\mathrm{2}\left({cos}^{\mathrm{4}} \theta\:+{sin}^{\mathrm{4}} \theta\right)\Rightarrow\frac{{x}^{\mathrm{4}} \:+{y}^{\mathrm{4}} }{{cos}^{\mathrm{4}} \theta\:+{sin}^{\mathrm{4}} \theta}\:=\frac{\mathrm{2}}{\mathrm{97}}\:{but} \\ $$$$\frac{{x}}{{sin}\theta}\:=\frac{{y}}{{cos}\theta}\:\Rightarrow\:\frac{{x}^{\mathrm{4}} }{{sin}^{\mathrm{4}} \theta}\:=\frac{{y}^{\mathrm{4}} }{{cos}^{\mathrm{4}} \theta}\:=\frac{{x}^{\mathrm{4}} \:+{y}^{\mathrm{4}} }{{sin}^{\mathrm{4}} \theta\:+{cos}^{\mathrm{4}} \theta}\:=\frac{\mathrm{2}}{\mathrm{97}}\:\Rightarrow \\ $$$${x}^{\mathrm{4}} \:=\frac{\mathrm{2}}{\mathrm{97}}\:{sin}^{\mathrm{4}} \theta\:\:{and}\:{y}^{\mathrm{4}} \:=\frac{\mathrm{2}}{\mathrm{97}}\:{cos}^{\mathrm{4}} \theta\:\Rightarrow{x}^{\mathrm{2}} \:=\sqrt{\frac{\mathrm{2}}{\mathrm{97}}}{sin}^{\mathrm{2}} \theta\:\:\:{and}\:{y}^{\mathrm{2}} \:=\sqrt{\frac{\mathrm{2}}{\mathrm{97}}}{cos}^{\mathrm{2}} \theta \\ $$$$ \\ $$$$\Rightarrow{x}^{\mathrm{2}\:} +{y}^{\mathrm{2}} \:=\sqrt{\frac{\mathrm{2}}{\mathrm{97}}}\:\:\:\:{but}\:{x}\:={k}\:{sin}\theta\:{and}\:{y}\:={kcos}\theta\:\Rightarrow{k}^{\mathrm{2}} \:=\sqrt{\frac{\mathrm{2}}{\mathrm{97}}}\:\Rightarrow \\ $$$${k}\:=^{\mathrm{4}} \sqrt{\frac{\mathrm{2}}{\mathrm{97}}}\:\Rightarrow\:\frac{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }{{xy}}\:=\frac{\sqrt{\frac{\mathrm{2}}{\mathrm{97}}}}{\left(^{\mathrm{4}} \sqrt{\frac{\mathrm{2}}{\mathrm{97}}}\right)\left(^{\mathrm{4}} \sqrt{\frac{\mathrm{2}}{\mathrm{97}}}\right){sin}\theta\:{cos}\theta}\:=\frac{\mathrm{1}}{{sin}\theta{cos}\theta} \\ $$
Commented by Tawa1 last updated on 03/Nov/18
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by maxmathsup by imad last updated on 03/Nov/18
$${you}\:{are}\:{welcome}\:{sir}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 03/Nov/18
![((sinθ)/x)=((cosθ)/y)=(1/k) x=ksinθ y=kcosθ x^2 +y^2 =k^2 ((cos^4 θ)/(k^4 sin^4 θ))+((sin^4 θ)/(k^4 cos^4 θ))=97 cot^4 θ+tan^4 θ=97k^4 (cot^2 θ+tan^2 θ)^2 −2=97k^4 {(cotθ+tanθ)^2 −2}^2 =97k^4 +2 (cotθ+tanθ)^2 =2+(√(97k^4 +2)) cotθ+tanθ=[2+(√(97k^4 +2)) ]^(1/2) (y/x)+(x/y)=[2+(√(97k^4 +2)) ]^(1/2) (y/x)+(x/y)=[2+(√(97(x^2 +y^2 )^2 +2)) ]^(1/2)](https://www.tinkutara.com/question/Q46958.png)
$$\frac{{sin}\theta}{{x}}=\frac{{cos}\theta}{{y}}=\frac{\mathrm{1}}{{k}} \\ $$$${x}={ksin}\theta\:\:\:{y}={kcos}\theta \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={k}^{\mathrm{2}} \\ $$$$\frac{{cos}^{\mathrm{4}} \theta}{{k}^{\mathrm{4}} {sin}^{\mathrm{4}} \theta}+\frac{{sin}^{\mathrm{4}} \theta}{{k}^{\mathrm{4}} {cos}^{\mathrm{4}} \theta}=\mathrm{97} \\ $$$${cot}^{\mathrm{4}} \theta+{tan}^{\mathrm{4}} \theta=\mathrm{97}{k}^{\mathrm{4}} \\ $$$$\left({cot}^{\mathrm{2}} \theta+{tan}^{\mathrm{2}} \theta\right)^{\mathrm{2}} −\mathrm{2}=\mathrm{97}{k}^{\mathrm{4}} \\ $$$$\left\{\left({cot}\theta+{tan}\theta\right)^{\mathrm{2}} −\mathrm{2}\right\}^{\mathrm{2}} =\mathrm{97}{k}^{\mathrm{4}} +\mathrm{2} \\ $$$$\left({cot}\theta+{tan}\theta\right)^{\mathrm{2}} =\mathrm{2}+\sqrt{\mathrm{97}{k}^{\mathrm{4}} +\mathrm{2}}\:\: \\ $$$${cot}\theta+{tan}\theta=\left[\mathrm{2}+\sqrt{\mathrm{97}{k}^{\mathrm{4}} +\mathrm{2}}\:\right]^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\frac{{y}}{{x}}+\frac{{x}}{{y}}=\left[\mathrm{2}+\sqrt{\mathrm{97}{k}^{\mathrm{4}} +\mathrm{2}}\:\right]^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\frac{{y}}{{x}}+\frac{{x}}{{y}}=\left[\mathrm{2}+\sqrt{\mathrm{97}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{2}}\:\right]^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$ \\ $$$$ \\ $$
Commented by Tawa1 last updated on 03/Nov/18
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 03/Nov/18

$${is}\:{it}\:{the}\:{answer}… \\ $$
Commented by Tawa1 last updated on 03/Nov/18
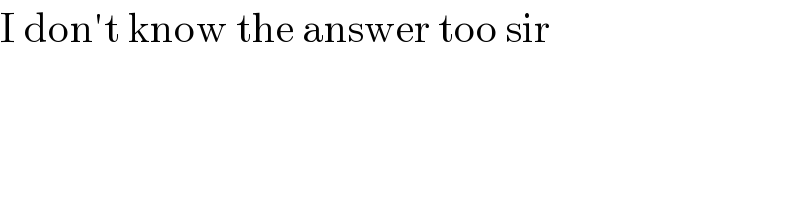
$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{too}\:\mathrm{sir} \\ $$
