Menu Close

Question-47026

Tinku Tara 0 Comments
Pin




Question Number 47026 by ajfour last updated on 04/Nov/18
Commented by ajfour last updated on 04/Nov/18
If the circle has unit radius and both coloured areas are equal, find the eq. of parabola.
$${If}\:{the}\:{circle}\:{has}\:{unit}\:{radius}\:{and} \\ $$$${both}\:{coloured}\:{areas}\:{are}\:{equal}, \\ $$$${find}\:{the}\:{eq}.\:{of}\:{parabola}. \\ $$
Commented by ajfour last updated on 04/Nov/18
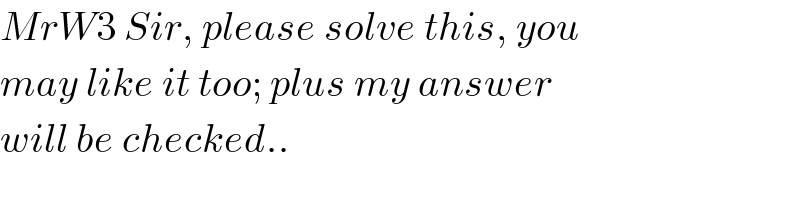
MrW3 Sir, please solve this, you may like it too; plus my answer will be checked..
$${MrW}\mathrm{3}\:{Sir},\:{please}\:{solve}\:{this},\:{you} \\ $$$${may}\:{like}\:{it}\:{too};\:{plus}\:{my}\:{answer} \\ $$$${will}\:{be}\:{checked}.. \\ $$
Commented by Meritguide1234 last updated on 04/Nov/18
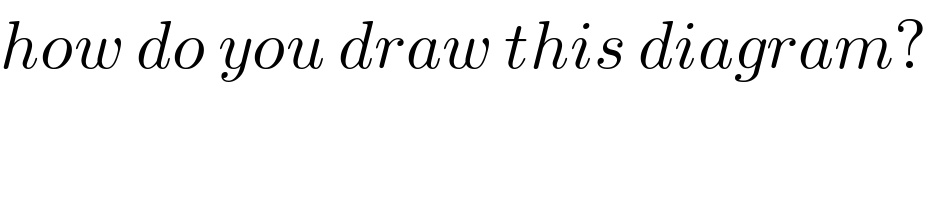
how do you draw this diagram?
$${how}\:{do}\:{you}\:{draw}\:{this}\:{diagram}? \\ $$
Commented by ajfour last updated on 04/Nov/18
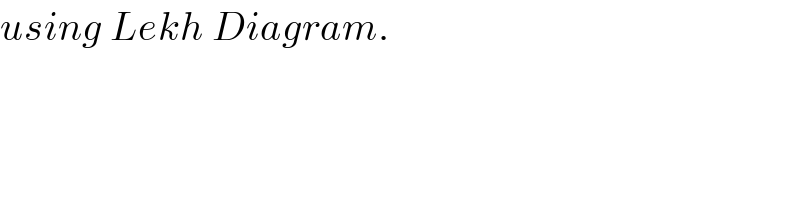
using Lekh Diagram.
$${using}\:{Lekh}\:{Diagram}. \\ $$
Answered by MrW3 last updated on 04/Nov/18
eqn. of parabola: y=ax^2 ⇒y′=2ax eqn. of circle: x^2 +(y−b)^2 =r^2 with r=1 ⇒x+(y−b)y′=0 let ar=λ contact points (±h,k) k=ah^2 ...(i) m=2ah ...(ii) h^2 +(k−b)^2 =r^2 ...(iii) h+(k−b)m=0 ...(iv) ⇒k−b=−(h/m)=−(1/(2a)) ⇒b=k+(1/(2a)) h^2 +(−(1/(2a)))^2 =r^2 h^2 =r^2 −(1/(4a^2 )) ⇒h=(√(r^2 −(1/(4a^2 ))))=r(√(1−(1/(4λ^2 )))) ⇒k=ah^2 =a(r^2 −(1/(4a^2 )))=r(ar−(1/(4ar)))=r(λ−(1/(4λ))) ⇒b=k+(1/(2a))=ar^2 +(1/(4a))=r(λ+(1/(4λ))) ⇒tan θ=m=2ah=2ar(√(1−(1/(4λ^2 ))))=(√(4λ^2 −1)) A_(yellow/2) =((2hk)/3)+(1/2)×r cos θ×r sin θ−((θr^2 )/2) A_(yellow/2) =((2r^2 )/3)(λ−(1/(4λ)))(√(1−(1/(4λ^2 ))))+((r^2 sin θ cos θ)/2)−((θr^2 )/2) A_(yellow/2) =A_(blue/2) =((πr^2 )/2) ((2r^2 )/3)(λ−(1/(4λ)))(√(1−(1/(4λ^2 ))))+((r^2 sin θ cos θ)/2)−((θr^2 )/2)=((πr^2 )/2) (4/3)(λ−(1/(4λ)))(√(1−(1/(4λ^2 ))))+sin θ cos θ−θ=π (4/3)(λ−(1/(4λ)))(√(1−(1/(4λ^2 ))))+((tan θ)/(1+tan^2 θ))−θ=π (((4λ)/3)−(1/(3λ)))(√(1−(1/(4λ^2 ))))+(1/(2λ))(√(1−(1/(4λ^2 ))))−tan^(−1) (√(4λ^2 −1))=π (1/3)(4λ+(1/(2λ)))(√(1−(1/(4λ^2 ))))−tan^(−1) (√(4λ^2 −1))=π (1/3)(2+(1/(4λ^2 )))(√(4λ^2 −1))−tan^(−1) (√(4λ^2 −1))=π ⇒λ=3.425 ⇒a=3.425 ⇒b=3.498
$${eqn}.\:{of}\:{parabola}: \\ $$$${y}={ax}^{\mathrm{2}} \\ $$$$\Rightarrow{y}'=\mathrm{2}{ax} \\ $$$$ \\ $$$${eqn}.\:{of}\:{circle}: \\ $$$${x}^{\mathrm{2}} +\left({y}−{b}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \:{with}\:{r}=\mathrm{1} \\ $$$$\Rightarrow{x}+\left({y}−{b}\right){y}'=\mathrm{0} \\ $$$$ \\ $$$${let}\:{ar}=\lambda \\ $$$$ \\ $$$${contact}\:{points}\:\left(\pm{h},{k}\right) \\ $$$${k}={ah}^{\mathrm{2}} \:\:\:…\left({i}\right) \\ $$$${m}=\mathrm{2}{ah}\:\:\:\:…\left({ii}\right) \\ $$$${h}^{\mathrm{2}} +\left({k}−{b}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \:\:\:…\left({iii}\right) \\ $$$${h}+\left({k}−{b}\right){m}=\mathrm{0}\:\:\:…\left({iv}\right) \\ $$$$\Rightarrow{k}−{b}=−\frac{{h}}{{m}}=−\frac{\mathrm{1}}{\mathrm{2}{a}} \\ $$$$\Rightarrow{b}={k}+\frac{\mathrm{1}}{\mathrm{2}{a}} \\ $$$${h}^{\mathrm{2}} +\left(−\frac{\mathrm{1}}{\mathrm{2}{a}}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$${h}^{\mathrm{2}} ={r}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}{a}^{\mathrm{2}} } \\ $$$$\Rightarrow{h}=\sqrt{{r}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}{a}^{\mathrm{2}} }}={r}\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}\lambda^{\mathrm{2}} }} \\ $$$$\Rightarrow{k}={ah}^{\mathrm{2}} ={a}\left({r}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}{a}^{\mathrm{2}} }\right)={r}\left({ar}−\frac{\mathrm{1}}{\mathrm{4}{ar}}\right)={r}\left(\lambda−\frac{\mathrm{1}}{\mathrm{4}\lambda}\right) \\ $$$$\Rightarrow{b}={k}+\frac{\mathrm{1}}{\mathrm{2}{a}}={ar}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}{a}}={r}\left(\lambda+\frac{\mathrm{1}}{\mathrm{4}\lambda}\right) \\ $$$$\Rightarrow\mathrm{tan}\:\theta={m}=\mathrm{2}{ah}=\mathrm{2}{ar}\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}\lambda^{\mathrm{2}} }}=\sqrt{\mathrm{4}\lambda^{\mathrm{2}} −\mathrm{1}} \\ $$$${A}_{{yellow}/\mathrm{2}} =\frac{\mathrm{2}{hk}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{2}}×{r}\:\mathrm{cos}\:\theta×{r}\:\mathrm{sin}\:\theta−\frac{\theta{r}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${A}_{{yellow}/\mathrm{2}} =\frac{\mathrm{2}{r}^{\mathrm{2}} }{\mathrm{3}}\left(\lambda−\frac{\mathrm{1}}{\mathrm{4}\lambda}\right)\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}\lambda^{\mathrm{2}} }}+\frac{{r}^{\mathrm{2}} \:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta}{\mathrm{2}}−\frac{\theta{r}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${A}_{{yellow}/\mathrm{2}} ={A}_{{blue}/\mathrm{2}} =\frac{\pi{r}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$ \\ $$$$\frac{\mathrm{2}{r}^{\mathrm{2}} }{\mathrm{3}}\left(\lambda−\frac{\mathrm{1}}{\mathrm{4}\lambda}\right)\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}\lambda^{\mathrm{2}} }}+\frac{{r}^{\mathrm{2}} \:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta}{\mathrm{2}}−\frac{\theta{r}^{\mathrm{2}} }{\mathrm{2}}=\frac{\pi{r}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\frac{\mathrm{4}}{\mathrm{3}}\left(\lambda−\frac{\mathrm{1}}{\mathrm{4}\lambda}\right)\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}\lambda^{\mathrm{2}} }}+\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta−\theta=\pi \\ $$$$\frac{\mathrm{4}}{\mathrm{3}}\left(\lambda−\frac{\mathrm{1}}{\mathrm{4}\lambda}\right)\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}\lambda^{\mathrm{2}} }}+\frac{\mathrm{tan}\:\theta}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta}−\theta=\pi \\ $$$$\left(\frac{\mathrm{4}\lambda}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}\lambda}\right)\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}\lambda^{\mathrm{2}} }}+\frac{\mathrm{1}}{\mathrm{2}\lambda}\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}\lambda^{\mathrm{2}} }}−\mathrm{tan}^{−\mathrm{1}} \sqrt{\mathrm{4}\lambda^{\mathrm{2}} −\mathrm{1}}=\pi \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{4}\lambda+\frac{\mathrm{1}}{\mathrm{2}\lambda}\right)\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}\lambda^{\mathrm{2}} }}−\mathrm{tan}^{−\mathrm{1}} \sqrt{\mathrm{4}\lambda^{\mathrm{2}} −\mathrm{1}}=\pi \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{2}+\frac{\mathrm{1}}{\mathrm{4}\lambda^{\mathrm{2}} }\right)\sqrt{\mathrm{4}\lambda^{\mathrm{2}} −\mathrm{1}}−\mathrm{tan}^{−\mathrm{1}} \sqrt{\mathrm{4}\lambda^{\mathrm{2}} −\mathrm{1}}=\pi \\ $$$$\Rightarrow\lambda=\mathrm{3}.\mathrm{425} \\ $$$$\Rightarrow{a}=\mathrm{3}.\mathrm{425} \\ $$$$\Rightarrow{b}=\mathrm{3}.\mathrm{498} \\ $$
Commented by ajfour last updated on 04/Nov/18
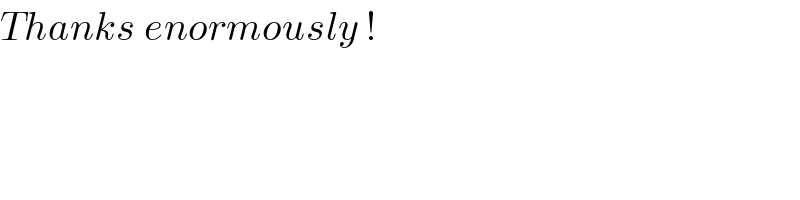
Thanks enormously !
$${Thanks}\:{enormously}\:! \\ $$
Answered by ajfour last updated on 04/Nov/18
Commented by ajfour last updated on 05/Nov/18
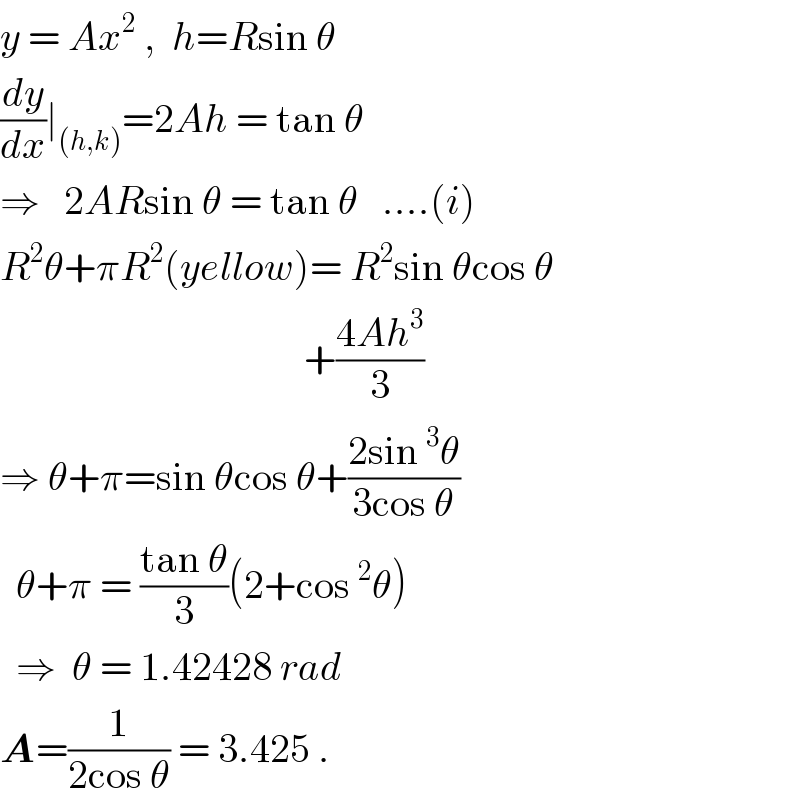
y = Ax^2 , h=Rsin θ (dy/dx)∣_((h,k)) =2Ah = tan θ ⇒ 2ARsin θ = tan θ ....(i) R^2 θ+πR^2 (yellow)= R^2 sin θcos θ +((4Ah^3 )/3) ⇒ θ+π=sin θcos θ+((2sin^3 θ)/(3cos θ)) θ+π = ((tan θ)/3)(2+cos^2 θ) ⇒ θ = 1.42428 rad A=(1/(2cos θ)) = 3.425 .
$${y}\:=\:{Ax}^{\mathrm{2}} \:,\:\:{h}={R}\mathrm{sin}\:\theta \\ $$$$\frac{{dy}}{{dx}}\mid_{\left({h},{k}\right)} =\mathrm{2}{Ah}\:=\:\mathrm{tan}\:\theta \\ $$$$\Rightarrow\:\:\:\mathrm{2}{AR}\mathrm{sin}\:\theta\:=\:\mathrm{tan}\:\theta\:\:\:….\left({i}\right) \\ $$$${R}^{\mathrm{2}} \theta+\pi{R}^{\mathrm{2}} \left({yellow}\right)=\:{R}^{\mathrm{2}} \mathrm{sin}\:\theta\mathrm{cos}\:\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\frac{\mathrm{4}{Ah}^{\mathrm{3}} }{\mathrm{3}} \\ $$$$\Rightarrow\:\theta+\pi=\mathrm{sin}\:\theta\mathrm{cos}\:\theta+\frac{\mathrm{2sin}\:^{\mathrm{3}} \theta}{\mathrm{3cos}\:\theta} \\ $$$$\:\:\theta+\pi\:=\:\frac{\mathrm{tan}\:\theta}{\mathrm{3}}\left(\mathrm{2}+\mathrm{cos}\:^{\mathrm{2}} \theta\right) \\ $$$$\:\:\Rightarrow\:\:\theta\:=\:\mathrm{1}.\mathrm{42428}\:{rad} \\ $$$$\boldsymbol{{A}}=\frac{\mathrm{1}}{\mathrm{2cos}\:\theta}\:=\:\mathrm{3}.\mathrm{425}\:. \\ $$
Commented by MrW3 last updated on 05/Nov/18
nice approach, short and direct! what is A in 3D case, i.e. blue and yellow volumns are the same?
$${nice}\:{approach},\:{short}\:{and}\:{direct}! \\ $$$${what}\:{is}\:{A}\:{in}\:\mathrm{3}{D}\:{case},\:{i}.{e}.\:{blue}\:{and} \\ $$$${yellow}\:{volumns}\:{are}\:{the}\:{same}? \\ $$
Commented by ajfour last updated on 09/Nov/18
z_P = Ar_P ^2 ; r_P = Rsin α (dz/dr) = tan α = 2ARsin α ⇒ 2ARcos α = 1 .....(I) z_P = AR^2 sin^2 α = (R/2)sin αtan α ..(II) yellow volume = blue volume 2π∫_0 ^( Rsin α) r{z_P +Rcos α−(√(R^2 −r^2 ))−Ar^2 )}dr = (4/3)πR^3 ⇒ [(z_P +Rcos α)(r^2 /2) + (((R^2 −r^2 )^(3/2) )/3) −((Ar^4 )/4)]_0 ^(Rsin α) = ((2R^3 )/3) (((sin^2 α)/(2cos α))+cos α)((sin^2 α)/2)−(((1−cos^3 α))/3) −((sin^4 α)/(8cos α)) = (2/3) dividing by cos^3 α , & with m= tan α (((m^2 +2)m^2 )/4)−(((1+m^2 )^(3/2) )/3)+(1/3) −(m^4 /8) = ((2(1+m^2 )^(3/2) )/3) ⇒ 3m^4 −24(1+m^2 )^(3/2) +12m^2 +8= 0 ⇒ m = 7.67754 A = (1/(2cos (tan^(−1) 7.67754))) ⇒ A= 3.8712 .
$${z}_{{P}} \:=\:{Ar}_{{P}} ^{\mathrm{2}} \:\:\:;\:\:{r}_{{P}} =\:{R}\mathrm{sin}\:\alpha \\ $$$$\:\:\frac{{dz}}{{dr}}\:=\:\mathrm{tan}\:\alpha\:=\:\mathrm{2}{AR}\mathrm{sin}\:\alpha \\ $$$$\Rightarrow\:\:\:\:\:\mathrm{2}{AR}\mathrm{cos}\:\alpha\:=\:\mathrm{1}\:\:\:\:…..\left({I}\right) \\ $$$${z}_{{P}} \:=\:{AR}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \alpha\:=\:\frac{{R}}{\mathrm{2}}\mathrm{sin}\:\alpha\mathrm{tan}\:\alpha\:\:\:..\left({II}\right) \\ $$$${yellow}\:{volume}\:=\:{blue}\:{volume} \\ $$$$\left.\mathrm{2}\pi\int_{\mathrm{0}} ^{\:\:{R}\mathrm{sin}\:\alpha} {r}\left\{{z}_{{P}} +{R}\mathrm{cos}\:\alpha−\sqrt{{R}^{\mathrm{2}} −{r}^{\mathrm{2}} }−{Ar}^{\mathrm{2}} \right)\right\}{dr}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{4}}{\mathrm{3}}\pi{R}^{\mathrm{3}} \\ $$$$\Rightarrow\:\:\left[\left({z}_{{P}} +{R}\mathrm{cos}\:\alpha\right)\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\:+\:\frac{\left({R}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} }{\mathrm{3}}\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:−\frac{{Ar}^{\mathrm{4}} }{\mathrm{4}}\right]_{\mathrm{0}} ^{{R}\mathrm{sin}\:\alpha} \:=\:\frac{\mathrm{2}{R}^{\mathrm{3}} }{\mathrm{3}} \\ $$$$\:\:\left(\frac{\mathrm{sin}\:^{\mathrm{2}} \alpha}{\mathrm{2cos}\:\alpha}+\mathrm{cos}\:\alpha\right)\frac{\mathrm{sin}\:^{\mathrm{2}} \alpha}{\mathrm{2}}−\frac{\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{3}} \alpha\right)}{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\frac{\mathrm{sin}\:^{\mathrm{4}} \alpha}{\mathrm{8cos}\:\alpha}\:=\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${dividing}\:{by}\:\mathrm{cos}\:^{\mathrm{3}} \alpha\:,\:\&\:{with}\: \\ $$$$\:\:\:{m}=\:\mathrm{tan}\:\alpha \\ $$$$\frac{\left({m}^{\mathrm{2}} +\mathrm{2}\right){m}^{\mathrm{2}} }{\mathrm{4}}−\frac{\left(\mathrm{1}+{m}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} }{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\frac{{m}^{\mathrm{4}} }{\mathrm{8}}\:=\:\frac{\mathrm{2}\left(\mathrm{1}+{m}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} }{\mathrm{3}} \\ $$$$\Rightarrow\:\mathrm{3}{m}^{\mathrm{4}} −\mathrm{24}\left(\mathrm{1}+{m}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} +\mathrm{12}{m}^{\mathrm{2}} +\mathrm{8}=\:\mathrm{0} \\ $$$$\Rightarrow\:\:{m}\:=\:\mathrm{7}.\mathrm{67754} \\ $$$$\:\:\:\:\:\:{A}\:=\:\frac{\mathrm{1}}{\mathrm{2cos}\:\left(\mathrm{tan}^{−\mathrm{1}} \mathrm{7}.\mathrm{67754}\right)} \\ $$$$\Rightarrow\:\:{A}=\:\mathrm{3}.\mathrm{8712}\:. \\ $$
Commented by ajfour last updated on 09/Nov/18
MrW Sir , please check this.
$${MrW}\:{Sir}\:,\:{please}\:{check}\:{this}. \\ $$
Commented by MrW3 last updated on 09/Nov/18
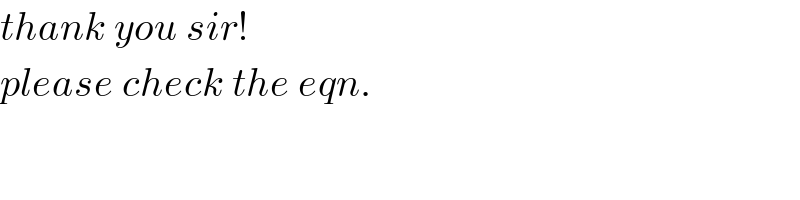
thank you sir! please check the eqn.
$${thank}\:{you}\:{sir}! \\ $$$${please}\:{check}\:{the}\:{eqn}. \\ $$
Answered by MJS last updated on 04/Nov/18
I turn it upside down and put parabola: y=−ax^2 +b; y′=−2ax circle: x^2 +(y+c)^2 =1 y=−c+(√(1−x^2 )) y′=−(x/( (√(1−x^2 )))) zeros x=±(√(1−c^2 )) slope of tangents in zeros s=∓((√(1−c^2 ))/c) parabola: zeros at x=±(√(1−c^2 )) −a(1−c^2 )+b=0 ⇒ b=a(1−c^2 ) slope=∓((√(1−c^2 ))/c) at x=±(√(1−c^2 )) ((√(1−c^2 ))/c)=2a(√(1−c^2 )) ⇒ a=(1/(2c)); b=((1−c^2 )/(2c)) parabola: y=−(x^2 /(2c))+((1−c^2 )/(2c)) −(1/(2c))∫_(−(√(1−c^2 ))) ^(√(1−c^2 )) (x^2 −1+c^2 )dx+∫_(−(√(1−c^2 ))) ^(√(1−c^2 )) (c−(√(1−x^2 )))dx= =(((2+c^2 )(√(1−c^2 )))/(3c))−arcsin (√(1−c^2 )) (((2+c^2 )(√(1−c^2 )))/(3c))−arcsin (√(1−c^2 ))=π ⇒ c=.145986 ⇒ a=3.42500 ⇒ b=3.35200
$$\mathrm{I}\:\mathrm{turn}\:\mathrm{it}\:\mathrm{upside}\:\mathrm{down}\:\mathrm{and}\:\mathrm{put} \\ $$$$\mathrm{parabola}:\:{y}=−{ax}^{\mathrm{2}} +{b};\:{y}'=−\mathrm{2}{ax} \\ $$$$\mathrm{circle}:\:{x}^{\mathrm{2}} +\left({y}+{c}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\:\:\:\:\:{y}=−{c}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:{y}'=−\frac{{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$$\mathrm{zeros} \\ $$$$\:\:\:\:\:{x}=\pm\sqrt{\mathrm{1}−{c}^{\mathrm{2}} } \\ $$$$\mathrm{slope}\:\mathrm{of}\:\mathrm{tangents}\:\mathrm{in}\:\mathrm{zeros} \\ $$$$\:\:\:\:\:{s}=\mp\frac{\sqrt{\mathrm{1}−{c}^{\mathrm{2}} }}{{c}} \\ $$$$\mathrm{parabola}:\:\mathrm{zeros}\:\mathrm{at}\:{x}=\pm\sqrt{\mathrm{1}−{c}^{\mathrm{2}} } \\ $$$$−{a}\left(\mathrm{1}−{c}^{\mathrm{2}} \right)+{b}=\mathrm{0}\:\Rightarrow\:{b}={a}\left(\mathrm{1}−{c}^{\mathrm{2}} \right) \\ $$$$\mathrm{slope}=\mp\frac{\sqrt{\mathrm{1}−{c}^{\mathrm{2}} }}{{c}}\:\mathrm{at}\:{x}=\pm\sqrt{\mathrm{1}−{c}^{\mathrm{2}} } \\ $$$$\frac{\sqrt{\mathrm{1}−{c}^{\mathrm{2}} }}{{c}}=\mathrm{2}{a}\sqrt{\mathrm{1}−{c}^{\mathrm{2}} }\:\Rightarrow\:{a}=\frac{\mathrm{1}}{\mathrm{2}{c}};\:{b}=\frac{\mathrm{1}−{c}^{\mathrm{2}} }{\mathrm{2}{c}} \\ $$$$\mathrm{parabola}:\:{y}=−\frac{{x}^{\mathrm{2}} }{\mathrm{2}{c}}+\frac{\mathrm{1}−{c}^{\mathrm{2}} }{\mathrm{2}{c}} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}{c}}\underset{−\sqrt{\mathrm{1}−{c}^{\mathrm{2}} }} {\overset{\sqrt{\mathrm{1}−{c}^{\mathrm{2}} }} {\int}}\left({x}^{\mathrm{2}} −\mathrm{1}+{c}^{\mathrm{2}} \right){dx}+\underset{−\sqrt{\mathrm{1}−{c}^{\mathrm{2}} }} {\overset{\sqrt{\mathrm{1}−{c}^{\mathrm{2}} }} {\int}}\left({c}−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right){dx}= \\ $$$$=\frac{\left(\mathrm{2}+{c}^{\mathrm{2}} \right)\sqrt{\mathrm{1}−{c}^{\mathrm{2}} }}{\mathrm{3}{c}}−\mathrm{arcsin}\:\sqrt{\mathrm{1}−{c}^{\mathrm{2}} } \\ $$$$\frac{\left(\mathrm{2}+{c}^{\mathrm{2}} \right)\sqrt{\mathrm{1}−{c}^{\mathrm{2}} }}{\mathrm{3}{c}}−\mathrm{arcsin}\:\sqrt{\mathrm{1}−{c}^{\mathrm{2}} }=\pi \\ $$$$\Rightarrow\:{c}=.\mathrm{145986} \\ $$$$\Rightarrow\:{a}=\mathrm{3}.\mathrm{42500} \\ $$$$\Rightarrow\:{b}=\mathrm{3}.\mathrm{35200} \\ $$
Commented by ajfour last updated on 05/Nov/18
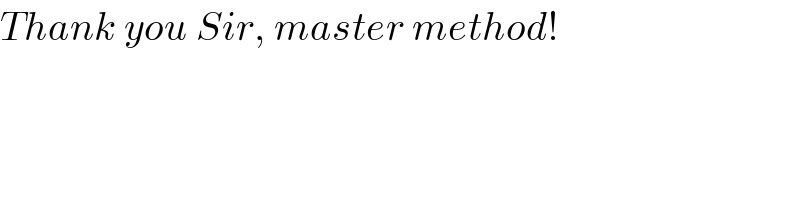
Thank you Sir, master method!
$${Thank}\:{you}\:{Sir},\:{master}\:{method}! \\ $$
Commented by MJS last updated on 09/Nov/18
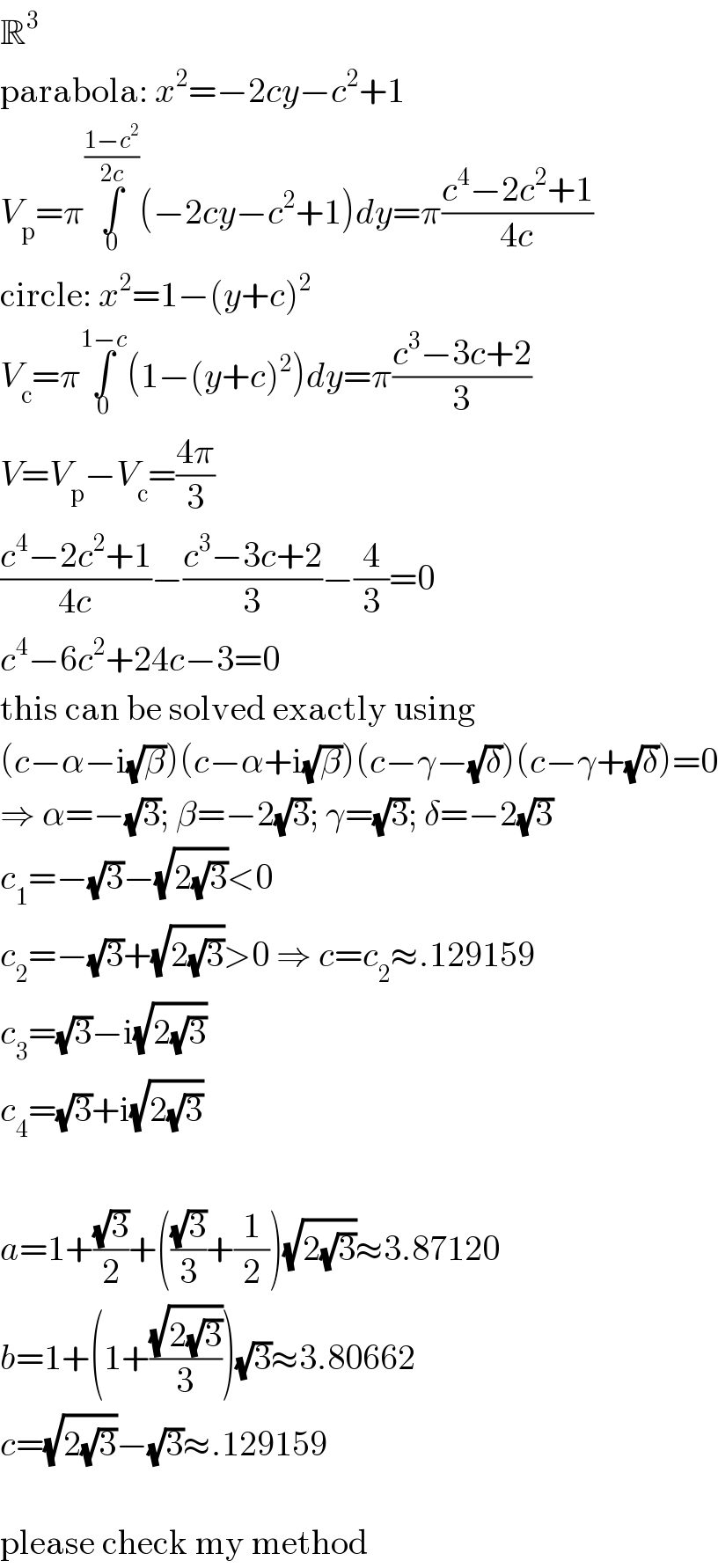
R^3 parabola: x^2 =−2cy−c^2 +1 V_p =π∫_0 ^((1−c^2 )/(2c)) (−2cy−c^2 +1)dy=π((c^4 −2c^2 +1)/(4c)) circle: x^2 =1−(y+c)^2 V_c =π∫_0 ^(1−c) (1−(y+c)^2 )dy=π((c^3 −3c+2)/3) V=V_p −V_c =((4π)/3) ((c^4 −2c^2 +1)/(4c))−((c^3 −3c+2)/3)−(4/3)=0 c^4 −6c^2 +24c−3=0 this can be solved exactly using (c−α−i(√β))(c−α+i(√β))(c−γ−(√δ))(c−γ+(√δ))=0 ⇒ α=−(√3); β=−2(√3); γ=(√3); δ=−2(√3) c_1 =−(√3)−(√(2(√3)))<0 c_2 =−(√3)+(√(2(√3)))>0 ⇒ c=c_2 ≈.129159 c_3 =(√3)−i(√(2(√3))) c_4 =(√3)+i(√(2(√3))) a=1+((√3)/2)+(((√3)/3)+(1/2))(√(2(√3)))≈3.87120 b=1+(1+((√(2(√3)))/3))(√3)≈3.80662 c=(√(2(√3)))−(√3)≈.129159 please check my method
$$\mathbb{R}^{\mathrm{3}} \\ $$$$\mathrm{parabola}:\:{x}^{\mathrm{2}} =−\mathrm{2}{cy}−{c}^{\mathrm{2}} +\mathrm{1} \\ $$$${V}_{\mathrm{p}} =\pi\underset{\mathrm{0}} {\overset{\frac{\mathrm{1}−{c}^{\mathrm{2}} }{\mathrm{2}{c}}} {\int}}\left(−\mathrm{2}{cy}−{c}^{\mathrm{2}} +\mathrm{1}\right){dy}=\pi\frac{{c}^{\mathrm{4}} −\mathrm{2}{c}^{\mathrm{2}} +\mathrm{1}}{\mathrm{4}{c}} \\ $$$$\mathrm{circle}:\:{x}^{\mathrm{2}} =\mathrm{1}−\left({y}+{c}\right)^{\mathrm{2}} \\ $$$${V}_{\mathrm{c}} =\pi\underset{\mathrm{0}} {\overset{\mathrm{1}−{c}} {\int}}\left(\mathrm{1}−\left({y}+{c}\right)^{\mathrm{2}} \right){dy}=\pi\frac{{c}^{\mathrm{3}} −\mathrm{3}{c}+\mathrm{2}}{\mathrm{3}} \\ $$$${V}={V}_{\mathrm{p}} −{V}_{\mathrm{c}} =\frac{\mathrm{4}\pi}{\mathrm{3}} \\ $$$$\frac{{c}^{\mathrm{4}} −\mathrm{2}{c}^{\mathrm{2}} +\mathrm{1}}{\mathrm{4}{c}}−\frac{{c}^{\mathrm{3}} −\mathrm{3}{c}+\mathrm{2}}{\mathrm{3}}−\frac{\mathrm{4}}{\mathrm{3}}=\mathrm{0} \\ $$$${c}^{\mathrm{4}} −\mathrm{6}{c}^{\mathrm{2}} +\mathrm{24}{c}−\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{this}\:\mathrm{can}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{exactly}\:\mathrm{using} \\ $$$$\left({c}−\alpha−\mathrm{i}\sqrt{\beta}\right)\left({c}−\alpha+\mathrm{i}\sqrt{\beta}\right)\left({c}−\gamma−\sqrt{\delta}\right)\left({c}−\gamma+\sqrt{\delta}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\alpha=−\sqrt{\mathrm{3}};\:\beta=−\mathrm{2}\sqrt{\mathrm{3}};\:\gamma=\sqrt{\mathrm{3}};\:\delta=−\mathrm{2}\sqrt{\mathrm{3}} \\ $$$${c}_{\mathrm{1}} =−\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}\sqrt{\mathrm{3}}}<\mathrm{0} \\ $$$${c}_{\mathrm{2}} =−\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}\sqrt{\mathrm{3}}}>\mathrm{0}\:\Rightarrow\:{c}={c}_{\mathrm{2}} \approx.\mathrm{129159} \\ $$$${c}_{\mathrm{3}} =\sqrt{\mathrm{3}}−\mathrm{i}\sqrt{\mathrm{2}\sqrt{\mathrm{3}}} \\ $$$${c}_{\mathrm{4}} =\sqrt{\mathrm{3}}+\mathrm{i}\sqrt{\mathrm{2}\sqrt{\mathrm{3}}} \\ $$$$ \\ $$$${a}=\mathrm{1}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{2}}\right)\sqrt{\mathrm{2}\sqrt{\mathrm{3}}}\approx\mathrm{3}.\mathrm{87120} \\ $$$${b}=\mathrm{1}+\left(\mathrm{1}+\frac{\sqrt{\mathrm{2}\sqrt{\mathrm{3}}}}{\mathrm{3}}\right)\sqrt{\mathrm{3}}\approx\mathrm{3}.\mathrm{80662} \\ $$$${c}=\sqrt{\mathrm{2}\sqrt{\mathrm{3}}}−\sqrt{\mathrm{3}}\approx.\mathrm{129159} \\ $$$$ \\ $$$$\mathrm{please}\:\mathrm{check}\:\mathrm{my}\:\mathrm{method} \\ $$
Commented by MrW3 last updated on 09/Nov/18
great sir! we get the same eqn. and result.
$${great}\:{sir}! \\ $$$${we}\:{get}\:{the}\:{same}\:{eqn}.\:{and}\:{result}. \\ $$
Answered by MrW3 last updated on 09/Nov/18
Commented by MrW3 last updated on 09/Nov/18
y=ax^2 y′=2ax m=tan θ=2ah ⇒h=((tan θ)/(2a))=R sin θ ⇒a=(1/(2R cos θ)) k=ah^2 =((R^2 sin^2 θ)/(2R cos θ))=((R sin θ tan θ)/2) V_(yellow) =πh^2 k−πR^2 (1−cos θ)^2 [R−((1−cos θ)/3)R]−2π∫_0 ^h ax^3 dx V_(yellow) =πh^2 k−πR^3 (1−cos θ)^2 (((2+cos θ)/3))−((πah^4 )/2) V_(yellow) =((πR^3 sin^3 θ tan θ)/2)−πR^3 (1−cos θ)^2 (((2+cos θ)/3))−((πR^3 sin^4 θ)/(4 cos θ))=((4πR^3 )/3) ((sin^3 θ tan θ)/2)−(1−cos θ)^2 (((2+cos θ)/3))−((sin^4 θ)/(4 cos θ))=(4/3) 3 sin^4 θ−4(1−cos θ)^2 (2+cos θ)cos θ=16 cos θ 3 sin^4 θ−24cos θ+12 cos^2 θ−4cos^4 θ=0 ⇒cos^4 θ−6 cos^2 θ+24cos θ−3=0 ⇒cos θ=0.1292⇒θ=82.576° ⇒a=(1/(2×0.1292))=3.87
$${y}={ax}^{\mathrm{2}} \\ $$$${y}'=\mathrm{2}{ax} \\ $$$${m}=\mathrm{tan}\:\theta=\mathrm{2}{ah} \\ $$$$\Rightarrow{h}=\frac{\mathrm{tan}\:\theta}{\mathrm{2}{a}}={R}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow{a}=\frac{\mathrm{1}}{\mathrm{2}{R}\:\mathrm{cos}\:\theta} \\ $$$${k}={ah}^{\mathrm{2}} =\frac{{R}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta}{\mathrm{2}{R}\:\mathrm{cos}\:\theta}=\frac{{R}\:\mathrm{sin}\:\theta\:\mathrm{tan}\:\theta}{\mathrm{2}} \\ $$$${V}_{{yellow}} =\pi{h}^{\mathrm{2}} {k}−\pi{R}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}\:\theta\right)^{\mathrm{2}} \left[{R}−\frac{\mathrm{1}−\mathrm{cos}\:\theta}{\mathrm{3}}{R}\right]−\mathrm{2}\pi\int_{\mathrm{0}} ^{{h}} {ax}^{\mathrm{3}} {dx} \\ $$$${V}_{{yellow}} =\pi{h}^{\mathrm{2}} {k}−\pi{R}^{\mathrm{3}} \left(\mathrm{1}−\mathrm{cos}\:\theta\right)^{\mathrm{2}} \left(\frac{\mathrm{2}+\mathrm{cos}\:\theta}{\mathrm{3}}\right)−\frac{\pi{ah}^{\mathrm{4}} }{\mathrm{2}} \\ $$$${V}_{{yellow}} =\frac{\pi{R}^{\mathrm{3}} \:\mathrm{sin}^{\mathrm{3}} \:\theta\:\mathrm{tan}\:\theta}{\mathrm{2}}−\pi{R}^{\mathrm{3}} \left(\mathrm{1}−\mathrm{cos}\:\theta\right)^{\mathrm{2}} \left(\frac{\mathrm{2}+\mathrm{cos}\:\theta}{\mathrm{3}}\right)−\frac{\pi{R}^{\mathrm{3}} \mathrm{sin}^{\mathrm{4}} \:\theta}{\mathrm{4}\:\mathrm{cos}\:\theta}=\frac{\mathrm{4}\pi{R}^{\mathrm{3}} }{\mathrm{3}} \\ $$$$\frac{\mathrm{sin}^{\mathrm{3}} \:\theta\:\mathrm{tan}\:\theta}{\mathrm{2}}−\left(\mathrm{1}−\mathrm{cos}\:\theta\right)^{\mathrm{2}} \left(\frac{\mathrm{2}+\mathrm{cos}\:\theta}{\mathrm{3}}\right)−\frac{\mathrm{sin}^{\mathrm{4}} \:\theta}{\mathrm{4}\:\mathrm{cos}\:\theta}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\mathrm{3}\:\mathrm{sin}^{\mathrm{4}} \:\theta−\mathrm{4}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)^{\mathrm{2}} \left(\mathrm{2}+\mathrm{cos}\:\theta\right)\mathrm{cos}\:\theta=\mathrm{16}\:\mathrm{cos}\:\theta \\ $$$$\mathrm{3}\:\mathrm{sin}^{\mathrm{4}} \:\theta−\mathrm{24cos}\:\theta+\mathrm{12}\:\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{4cos}^{\mathrm{4}} \:\theta=\mathrm{0} \\ $$$$\Rightarrow\mathrm{cos}^{\mathrm{4}} \:\theta−\mathrm{6}\:\mathrm{cos}^{\mathrm{2}} \:\theta+\mathrm{24cos}\:\theta−\mathrm{3}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{cos}\:\theta=\mathrm{0}.\mathrm{1292}\Rightarrow\theta=\mathrm{82}.\mathrm{576}° \\ $$$$\Rightarrow{a}=\frac{\mathrm{1}}{\mathrm{2}×\mathrm{0}.\mathrm{1292}}=\mathrm{3}.\mathrm{87} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *