Question Number 47243 by MrW3 last updated on 06/Nov/18

Answered by MJS last updated on 07/Nov/18
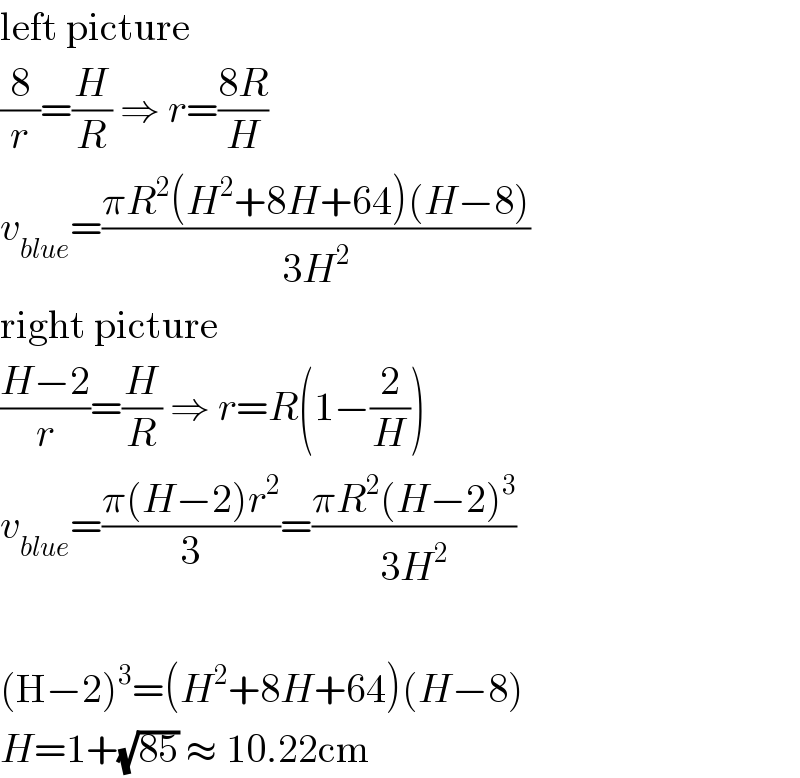
$$\mathrm{left}\:\mathrm{picture} \\ $$$$\frac{\mathrm{8}}{{r}}=\frac{{H}}{{R}}\:\Rightarrow\:{r}=\frac{\mathrm{8}{R}}{{H}} \\ $$$${v}_{{blue}} =\frac{\pi{R}^{\mathrm{2}} \left({H}^{\mathrm{2}} +\mathrm{8}{H}+\mathrm{64}\right)\left({H}−\mathrm{8}\right)}{\mathrm{3}{H}^{\mathrm{2}} } \\ $$$$\mathrm{right}\:\mathrm{picture} \\ $$$$\frac{{H}−\mathrm{2}}{{r}}=\frac{{H}}{{R}}\:\Rightarrow\:{r}={R}\left(\mathrm{1}−\frac{\mathrm{2}}{{H}}\right) \\ $$$${v}_{{blue}} =\frac{\pi\left({H}−\mathrm{2}\right){r}^{\mathrm{2}} }{\mathrm{3}}=\frac{\pi{R}^{\mathrm{2}} \left({H}−\mathrm{2}\right)^{\mathrm{3}} }{\mathrm{3}{H}^{\mathrm{2}} } \\ $$$$ \\ $$$$\left(\mathrm{H}−\mathrm{2}\right)^{\mathrm{3}} =\left({H}^{\mathrm{2}} +\mathrm{8}{H}+\mathrm{64}\right)\left({H}−\mathrm{8}\right) \\ $$$${H}=\mathrm{1}+\sqrt{\mathrm{85}}\:\approx\:\mathrm{10}.\mathrm{22cm} \\ $$
Commented by MrW3 last updated on 07/Nov/18

$${thank}\:{you}\:{sir}! \\ $$
