Question Number 47282 by behi83417@gmail.com last updated on 07/Nov/18
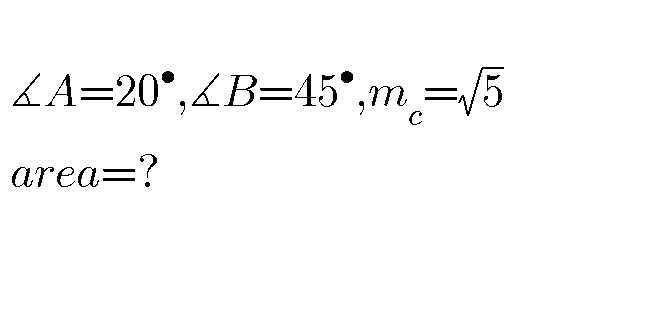
Answered by MrW3 last updated on 07/Nov/18
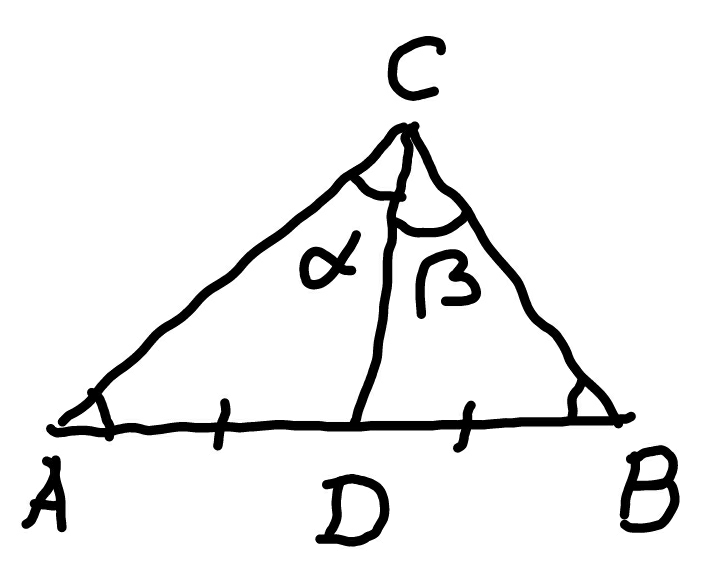
Commented by MrW3 last updated on 08/Nov/18

$${AB}={c} \\ $$$${AD}={DB}=\frac{{c}}{\mathrm{2}} \\ $$$${CD}={m}_{{c}} \\ $$$${let}\:\lambda=\frac{{c}}{\mathrm{2}{m}_{{c}} } \\ $$$$\frac{{m}_{{c}} }{\mathrm{sin}\:{A}}=\frac{{c}}{\mathrm{2}\:\mathrm{sin}\:\alpha} \\ $$$$\Rightarrow\mathrm{sin}\:\alpha=\frac{{c}}{\mathrm{2}{m}_{{c}} }\:\mathrm{sin}\:{A}=\lambda\:\mathrm{sin}\:{A} \\ $$$${similarly} \\ $$$$\mathrm{sin}\:\beta=\lambda\:\mathrm{sin}\:{B} \\ $$$$\alpha+\beta=\angle{C}=\pi−\left(\angle{A}+\angle{B}\right) \\ $$$$\Rightarrow\mathrm{sin}\:\left(\alpha+\beta\right)=\mathrm{sin}\:\left({A}+{B}\right) \\ $$$$\Rightarrow\mathrm{sin}\:\alpha\:\mathrm{cos}\:\beta+\mathrm{cos}\:\alpha\:\mathrm{sin}\:\beta=\mathrm{sin}\:\left({A}+{B}\right) \\ $$$$\Rightarrow\lambda\left(\mathrm{sin}\:{A}\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:{B}}+\mathrm{sin}\:{B}\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:{A}}\right)=\mathrm{sin}\:\left({A}+{B}\right) \\ $$$${A}=\mathrm{20}°,\:{B}=\mathrm{45}° \\ $$$${A}+{B}=\mathrm{65}°\neq\mathrm{90}° \\ $$$$\Rightarrow\lambda=\mathrm{1}\:\left({not}\:{suitable}\:{since}\:{A}+{B}\neq\mathrm{90}°\right) \\ $$$$\Rightarrow\lambda=\mathrm{1}.\mathrm{4112} \\ $$$$\Rightarrow{c}=\mathrm{2}×\mathrm{1}.\mathrm{4112}×\sqrt{\mathrm{5}}=\mathrm{6}.\mathrm{3111} \\ $$$$\frac{{h}}{\mathrm{tan}\:{A}}+\frac{{h}}{\mathrm{tan}\:{B}}={c} \\ $$$$\Rightarrow{h}=\frac{{c}}{\mathrm{cot}\:{A}+\mathrm{cot}\:{B}}=\mathrm{1}.\mathrm{6841} \\ $$$${A}_{\Delta{ABC}} =\frac{\mathrm{1}}{\mathrm{2}}{ch}=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{6}.\mathrm{3111}×\mathrm{1}.\mathrm{6841} \\ $$$$=\mathrm{5}.\mathrm{314}. \\ $$
Commented by behi83417@gmail.com last updated on 07/Nov/18
$${thanks}\:{in}\:{advance}\:{dear}\:{master}. \\ $$
Answered by behi83417@gmail.com last updated on 07/Nov/18
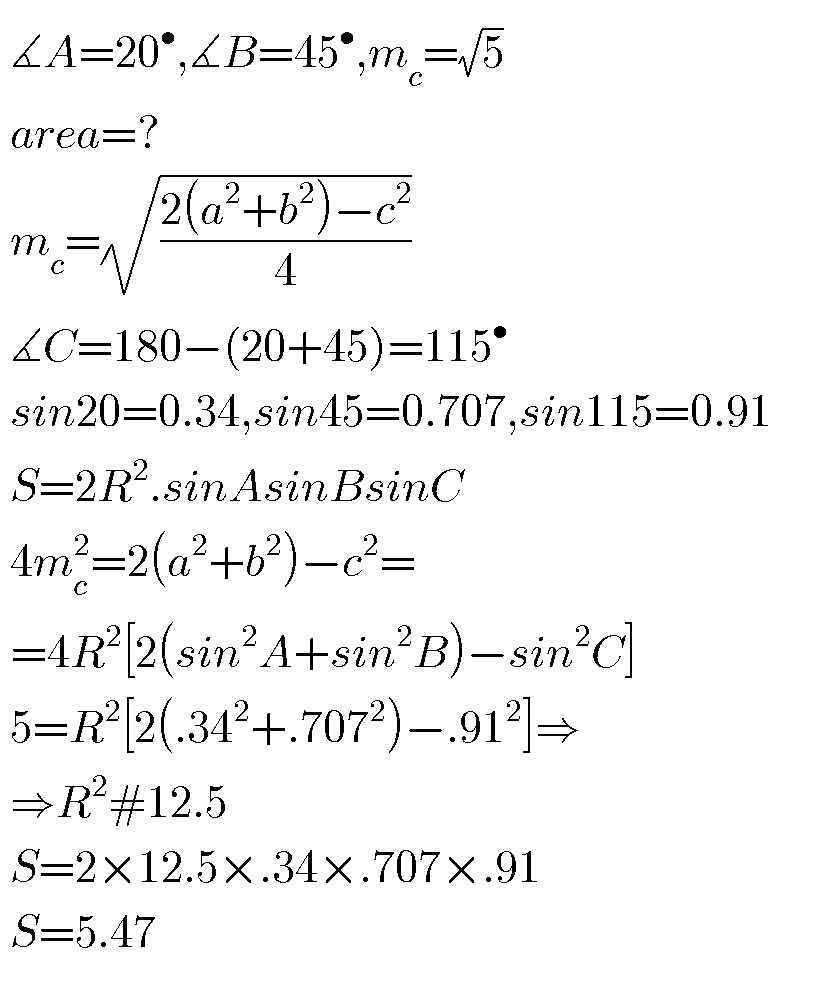
Commented by MrW3 last updated on 08/Nov/18

$${nice}\:{method}\:{sir}! \\ $$
