Question Number 47311 by Meritguide1234 last updated on 08/Nov/18
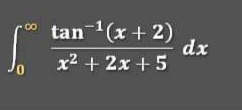
Commented by maxmathsup by imad last updated on 09/Nov/18
![changement x+2=t give ∫_0 ^∞ ((arctan(x+2))/(x^2 +2x+5))dx =∫_2 ^(+∞) ((arctan(t))/((t−2)^2 +2(t−2)+5))dt =∫_2 ^(+∞) ((arctant)/(t^2 −4t+4 +2t−4+5))dt =∫_2 ^(+∞) ((arctan(t))/(t^2 −2t +9))dt =∫_2 ^(+∞) ((arctan(t))/((t−1)^2 +8))dt =_(t−1=2(√2)u) ∫_(1/(2(√2))) ^(+∞) ((arctan(1+2(√2)u))/(8(1+u^2 ))) 2(√2)du =((√2)/4) ∫_((√2)/4) ^(+∞) ((arctan(1+2(√2)u))/(1+u^2 ))dt by parts ∫_((√2)/4) ^(+∞) ((arctan(1+2(√2)u))/(1+u^2 ))du =[arctanu.arctan(1+2(√2)u)]_((√2)/4) ^(+∞) −∫_((√2)/4) ^(+∞) ((arctanu)/(1+(1+2(√2)u)^2 )) 2(√2)du =(π^2 /4) −arctan(((√2)/4))arctan(2) −2(√2)∫_((√2)/4) ^(+∞) ((arctanu)/(1+1+4(√2)u +8u^2 ))du =(π^2 /4) −arctan(((√2)/4))arctan(2)−(√2)∫_((√2)/4) ^(+∞) ((arctan(u))/(1+2(√2)u +4u^2 ))du...be continued...](https://www.tinkutara.com/question/Q47390.png)
$${changement}\:{x}+\mathrm{2}={t}\:{give}\: \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left({x}+\mathrm{2}\right)}{{x}^{\mathrm{2}} \:+\mathrm{2}{x}+\mathrm{5}}{dx}\:=\int_{\mathrm{2}} ^{+\infty} \:\:\frac{{arctan}\left({t}\right)}{\left({t}−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{2}\left({t}−\mathrm{2}\right)+\mathrm{5}}{dt} \\ $$$$=\int_{\mathrm{2}} ^{+\infty} \:\:\frac{{arctant}}{{t}^{\mathrm{2}} −\mathrm{4}{t}+\mathrm{4}\:+\mathrm{2}{t}−\mathrm{4}+\mathrm{5}}{dt}\:=\int_{\mathrm{2}} ^{+\infty} \:\:\:\frac{{arctan}\left({t}\right)}{{t}^{\mathrm{2}} −\mathrm{2}{t}\:+\mathrm{9}}{dt} \\ $$$$=\int_{\mathrm{2}} ^{+\infty} \:\:\:\frac{{arctan}\left({t}\right)}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{8}}{dt}\:\:\:=_{{t}−\mathrm{1}=\mathrm{2}\sqrt{\mathrm{2}}{u}} \:\int_{\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}} ^{+\infty} \:\:\:\frac{{arctan}\left(\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}{u}\right)}{\mathrm{8}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\:\mathrm{2}\sqrt{\mathrm{2}}{du} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\:\int_{\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}} ^{+\infty} \:\:\:\frac{{arctan}\left(\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}{u}\right)}{\mathrm{1}+{u}^{\mathrm{2}} }{dt}\:{by}\:{parts}\:\: \\ $$$$\int_{\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}} ^{+\infty} \:\frac{{arctan}\left(\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}{u}\right)}{\mathrm{1}+{u}^{\mathrm{2}} }{du}\:=\left[{arctanu}.{arctan}\left(\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}{u}\right)\right]_{\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}} ^{+\infty} \\ $$$$−\int_{\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}} ^{+\infty} \:\:\:\:\frac{{arctanu}}{\mathrm{1}+\left(\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}{u}\right)^{\mathrm{2}} }\:\mathrm{2}\sqrt{\mathrm{2}}{du} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\:−{arctan}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\right){arctan}\left(\mathrm{2}\right)\:−\mathrm{2}\sqrt{\mathrm{2}}\int_{\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}} ^{+\infty} \:\:\frac{{arctanu}}{\mathrm{1}+\mathrm{1}+\mathrm{4}\sqrt{\mathrm{2}}{u}\:+\mathrm{8}{u}^{\mathrm{2}} }{du} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\:−{arctan}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\right){arctan}\left(\mathrm{2}\right)−\sqrt{\mathrm{2}}\int_{\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}} ^{+\infty} \:\:\:\:\frac{{arctan}\left({u}\right)}{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}{u}\:+\mathrm{4}{u}^{\mathrm{2}} }{du}…{be}\:{continued}… \\ $$
