Question Number 47342 by ajfour last updated on 08/Nov/18

Commented by ajfour last updated on 08/Nov/18

$${Find}\:{the}\:{Tension}\:{in}\:{rope}\left({light}\right)\:{if}\: \\ $$$${all}\:{surfaces}\:{are}\:{frictioness}. \\ $$
Answered by MrW3 last updated on 08/Nov/18
![a_1 =acceleration of wedge (→) a_2 =acceleration of small block on ground (←) a_3 =acceleration of small block on wedge (↙) a_3 =a_1 +a_2 T=m_o a_2 mg sin β−T=m(a_3 −a_1 cos β)=m[(1−cos β)a_1 +a_2 ] mg cos β−N=ma_1 sin β ⇒N=m(g cos β−a_1 sin β) T−T cos β+N sin β=Ma_1 T(1−cos β)+m(g cos β−a_1 sin β)sin β=Ma_1 m_0 a_2 (1−cos β)+m(g cos β−a_1 sin β)sin β=Ma_1 ⇒(M+m sin^2 β)a_1 −m_0 (1−cos β)a_2 =mg cos βsin β ...(i) ⇒m(1−cos β)a_1 +(m+m_0 )a_2 =mg sin β ...(ii) ⇒[(m+m_0 )(M+m sin^2 β)+m_0 m(1−cos β)^2 ]a_2 =mg sin β[M+m(1−cos β)] ⇒a_2 =((mg sin β[M+m(1−cos β)])/((m+m_0 )(M+m sin^2 β)+m_0 m(1−cos β)^2 )) ⇒T=((m_0 m[M+m(1−cos β)]g sin β)/((m+m_0 )(M+m sin^2 β)+m_0 m(1−cos β)^2 ))](https://www.tinkutara.com/question/Q47352.png)
$${a}_{\mathrm{1}} ={acceleration}\:{of}\:{wedge}\:\left(\rightarrow\right) \\ $$$${a}_{\mathrm{2}} ={acceleration}\:{of}\:{small}\:{block}\:{on}\:{ground}\:\left(\leftarrow\right) \\ $$$${a}_{\mathrm{3}} ={acceleration}\:{of}\:{small}\:{block}\:{on}\:{wedge}\:\left(\swarrow\right) \\ $$$${a}_{\mathrm{3}} ={a}_{\mathrm{1}} +{a}_{\mathrm{2}} \\ $$$${T}={m}_{{o}} {a}_{\mathrm{2}} \\ $$$${mg}\:\mathrm{sin}\:\beta−{T}={m}\left({a}_{\mathrm{3}} −{a}_{\mathrm{1}} \mathrm{cos}\:\beta\right)={m}\left[\left(\mathrm{1}−\mathrm{cos}\:\beta\right){a}_{\mathrm{1}} +{a}_{\mathrm{2}} \right] \\ $$$${mg}\:\mathrm{cos}\:\beta−{N}={ma}_{\mathrm{1}} \mathrm{sin}\:\beta \\ $$$$\Rightarrow{N}={m}\left({g}\:\mathrm{cos}\:\beta−{a}_{\mathrm{1}} \mathrm{sin}\:\beta\right) \\ $$$${T}−{T}\:\mathrm{cos}\:\beta+{N}\:\mathrm{sin}\:\beta={Ma}_{\mathrm{1}} \\ $$$${T}\left(\mathrm{1}−\mathrm{cos}\:\beta\right)+{m}\left({g}\:\mathrm{cos}\:\beta−{a}_{\mathrm{1}} \mathrm{sin}\:\beta\right)\mathrm{sin}\:\beta={Ma}_{\mathrm{1}} \\ $$$${m}_{\mathrm{0}} {a}_{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}\:\beta\right)+{m}\left({g}\:\mathrm{cos}\:\beta−{a}_{\mathrm{1}} \mathrm{sin}\:\beta\right)\mathrm{sin}\:\beta={Ma}_{\mathrm{1}} \\ $$$$\Rightarrow\left({M}+{m}\:\mathrm{sin}^{\mathrm{2}} \:\beta\right){a}_{\mathrm{1}} −{m}_{\mathrm{0}} \left(\mathrm{1}−\mathrm{cos}\:\beta\right){a}_{\mathrm{2}} ={mg}\:\mathrm{cos}\:\beta\mathrm{sin}\:\beta\:\:\:…\left({i}\right) \\ $$$$\Rightarrow{m}\left(\mathrm{1}−\mathrm{cos}\:\beta\right){a}_{\mathrm{1}} +\left({m}+{m}_{\mathrm{0}} \right){a}_{\mathrm{2}} ={mg}\:\mathrm{sin}\:\beta\:\:\:…\left({ii}\right) \\ $$$$ \\ $$$$\Rightarrow\left[\left({m}+{m}_{\mathrm{0}} \right)\left({M}+{m}\:\mathrm{sin}^{\mathrm{2}} \:\beta\right)+{m}_{\mathrm{0}} {m}\left(\mathrm{1}−\mathrm{cos}\:\beta\right)^{\mathrm{2}} \right]{a}_{\mathrm{2}} ={mg}\:\mathrm{sin}\:\beta\left[{M}+{m}\left(\mathrm{1}−\mathrm{cos}\:\beta\right)\right] \\ $$$$\Rightarrow{a}_{\mathrm{2}} =\frac{{mg}\:\mathrm{sin}\:\beta\left[{M}+{m}\left(\mathrm{1}−\mathrm{cos}\:\beta\right)\right]}{\left({m}+{m}_{\mathrm{0}} \right)\left({M}+{m}\:\mathrm{sin}^{\mathrm{2}} \:\beta\right)+{m}_{\mathrm{0}} {m}\left(\mathrm{1}−\mathrm{cos}\:\beta\right)^{\mathrm{2}} } \\ $$$$\Rightarrow{T}=\frac{{m}_{\mathrm{0}} {m}\left[{M}+{m}\left(\mathrm{1}−\mathrm{cos}\:\beta\right)\right]{g}\:\mathrm{sin}\:\beta}{\left({m}+{m}_{\mathrm{0}} \right)\left({M}+{m}\:\mathrm{sin}^{\mathrm{2}} \:\beta\right)+{m}_{\mathrm{0}} {m}\left(\mathrm{1}−\mathrm{cos}\:\beta\right)^{\mathrm{2}} } \\ $$
Commented by ajfour last updated on 09/Nov/18
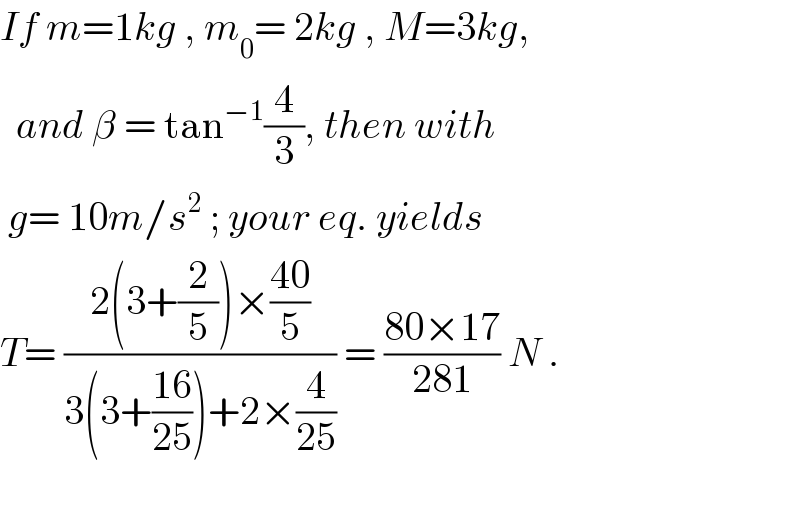
$${If}\:{m}=\mathrm{1}{kg}\:,\:{m}_{\mathrm{0}} =\:\mathrm{2}{kg}\:,\:{M}=\mathrm{3}{kg}, \\ $$$$\:\:{and}\:\beta\:=\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{4}}{\mathrm{3}},\:{then}\:{with}\: \\ $$$$\:{g}=\:\mathrm{10}{m}/{s}^{\mathrm{2}} \:;\:{your}\:{eq}.\:{yields} \\ $$$${T}=\:\frac{\mathrm{2}\left(\mathrm{3}+\frac{\mathrm{2}}{\mathrm{5}}\right)×\frac{\mathrm{40}}{\mathrm{5}}}{\mathrm{3}\left(\mathrm{3}+\frac{\mathrm{16}}{\mathrm{25}}\right)+\mathrm{2}×\frac{\mathrm{4}}{\mathrm{25}}}\:=\:\frac{\mathrm{80}×\mathrm{17}}{\mathrm{281}}\:{N}\:. \\ $$$$ \\ $$
Commented by ajfour last updated on 09/Nov/18

$${Thank}\:{you}\:{Sir}. \\ $$
Answered by ajfour last updated on 09/Nov/18
![T=(M+m)A−m(A+a_0 )cos β = m_0 a_0 mgsin β−T = m[(A+a_0 )−Acos β] Adding ⇒ mgsin β=ma_0 (1−cos β)+MA +2mA(1−cos β) ⇒ mgsin β=ma_0 (1−cos β) +A[M+2m(1−cos β)] ⇒ mgsin β=ma_0 (1−cos β) +((a_0 (m_0 +mcos β)[M+2m(1−cos β))/(M+m(1−cos β))) a_0 =((mgsin β[M+m(1−cos β)])/(m(1−cos β)[M+m(1−cos β)]+(m_0 +mcos β)[M+2m(1−cos β)])) T= ((mm_0 gsin β[M+m(1−cos β)])/(m(1−cos β)[M+m(1−cos β)]+(m_0 +mcos β)[M+2m(1−cos β)])) If m=1kg , m_0 = 2kg , M=3kg and β = tan^(−1) (4/3) T = ((20×(4/5)(3+(2/5)))/((2/5)(3+(2/5))+(2+(3/5))(3+(4/5)))) = ((80×17)/(34+13×19)) = ((80×17)/(281)) N .](https://www.tinkutara.com/question/Q47372.png)
$${T}=\left({M}+{m}\right){A}−{m}\left({A}+{a}_{\mathrm{0}} \right)\mathrm{cos}\:\beta \\ $$$$\:\:\:=\:{m}_{\mathrm{0}} {a}_{\mathrm{0}} \\ $$$${mg}\mathrm{sin}\:\beta−{T}\:=\:{m}\left[\left({A}+{a}_{\mathrm{0}} \right)−{A}\mathrm{cos}\:\beta\right] \\ $$$${Adding} \\ $$$$\Rightarrow\:{mg}\mathrm{sin}\:\beta={ma}_{\mathrm{0}} \left(\mathrm{1}−\mathrm{cos}\:\beta\right)+{MA} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{2}{mA}\left(\mathrm{1}−\mathrm{cos}\:\beta\right) \\ $$$$\Rightarrow\:{mg}\mathrm{sin}\:\beta={ma}_{\mathrm{0}} \left(\mathrm{1}−\mathrm{cos}\:\beta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:+{A}\left[{M}+\mathrm{2}{m}\left(\mathrm{1}−\mathrm{cos}\:\beta\right)\right] \\ $$$$ \\ $$$$\Rightarrow\:{mg}\mathrm{sin}\:\beta={ma}_{\mathrm{0}} \left(\mathrm{1}−\mathrm{cos}\:\beta\right) \\ $$$$\:\:\:+\frac{{a}_{\mathrm{0}} \left({m}_{\mathrm{0}} +{m}\mathrm{cos}\:\beta\right)\left[{M}+\mathrm{2}{m}\left(\mathrm{1}−\mathrm{cos}\:\beta\right)\right.}{{M}+{m}\left(\mathrm{1}−\mathrm{cos}\:\beta\right)} \\ $$$$ \\ $$$${a}_{\mathrm{0}} =\frac{{mg}\mathrm{sin}\:\beta\left[{M}+{m}\left(\mathrm{1}−\mathrm{cos}\:\beta\right)\right]}{{m}\left(\mathrm{1}−\mathrm{cos}\:\beta\right)\left[{M}+{m}\left(\mathrm{1}−\mathrm{cos}\:\beta\right)\right]+\left({m}_{\mathrm{0}} +{m}\mathrm{cos}\:\beta\right)\left[{M}+\mathrm{2}{m}\left(\mathrm{1}−\mathrm{cos}\:\beta\right)\right]} \\ $$$${T}=\:\frac{{mm}_{\mathrm{0}} {g}\mathrm{sin}\:\beta\left[{M}+{m}\left(\mathrm{1}−\mathrm{cos}\:\beta\right)\right]}{{m}\left(\mathrm{1}−\mathrm{cos}\:\beta\right)\left[{M}+{m}\left(\mathrm{1}−\mathrm{cos}\:\beta\right)\right]+\left({m}_{\mathrm{0}} +{m}\mathrm{cos}\:\beta\right)\left[{M}+\mathrm{2}{m}\left(\mathrm{1}−\mathrm{cos}\:\beta\right)\right]} \\ $$$${If}\:{m}=\mathrm{1}{kg}\:\:,\:{m}_{\mathrm{0}} =\:\mathrm{2}{kg}\:,\:{M}=\mathrm{3}{kg} \\ $$$$\:\:{and}\:\:\beta\:=\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{4}}{\mathrm{3}} \\ $$$${T}\:=\:\frac{\mathrm{20}×\frac{\mathrm{4}}{\mathrm{5}}\left(\mathrm{3}+\frac{\mathrm{2}}{\mathrm{5}}\right)}{\frac{\mathrm{2}}{\mathrm{5}}\left(\mathrm{3}+\frac{\mathrm{2}}{\mathrm{5}}\right)+\left(\mathrm{2}+\frac{\mathrm{3}}{\mathrm{5}}\right)\left(\mathrm{3}+\frac{\mathrm{4}}{\mathrm{5}}\right)} \\ $$$$\:\:\:\:=\:\frac{\mathrm{80}×\mathrm{17}}{\mathrm{34}+\mathrm{13}×\mathrm{19}}\:=\:\frac{\mathrm{80}×\mathrm{17}}{\mathrm{281}}\:{N}\:. \\ $$$$ \\ $$
