Question Number 47350 by behi83417@gmail.com last updated on 08/Nov/18

Commented by behi83417@gmail.com last updated on 08/Nov/18
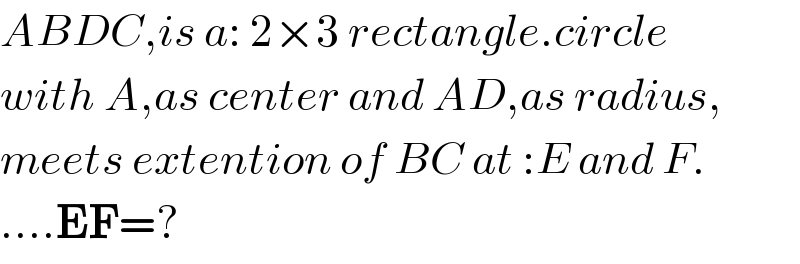
$${ABDC},{is}\:{a}:\:\mathrm{2}×\mathrm{3}\:{rectangle}.{circle} \\ $$$${with}\:{A},{as}\:{center}\:{and}\:{AD},{as}\:{radius}, \\ $$$${meets}\:{extention}\:{of}\:{BC}\:{at}\::{E}\:{and}\:{F}. \\ $$$$….\boldsymbol{\mathrm{EF}}=? \\ $$
Answered by MJS last updated on 09/Nov/18

$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$$${CD}:\:{y}=−\frac{{b}}{{a}}{x}+{b} \\ $$$${x}^{\mathrm{2}} +\left(−\frac{{b}}{{a}}{x}+{b}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} −\frac{\mathrm{2}{ab}^{\mathrm{2}} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{x}−\frac{{a}^{\mathrm{4}} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }=\mathrm{0} \\ $$$${x}=\frac{{a}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\left({b}^{\mathrm{2}} \pm\sqrt{{a}^{\mathrm{4}} +{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{4}} }\right) \\ $$$${y}={b}\left(\mathrm{1}−\frac{\mathrm{1}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\left({b}^{\mathrm{2}} \pm\sqrt{{a}^{\mathrm{4}} +{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{4}} }\right)\right) \\ $$$${E}=\begin{pmatrix}{\frac{{a}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\left({b}^{\mathrm{2}} −\sqrt{{a}^{\mathrm{4}} +{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{4}} }\right)}\\{{b}\left(\mathrm{1}−\frac{\mathrm{1}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\left({b}^{\mathrm{2}} −\sqrt{{a}^{\mathrm{4}} +{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{4}} }\right)\right)}\end{pmatrix} \\ $$$${F}=\begin{pmatrix}{\frac{{a}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\left({b}^{\mathrm{2}} +\sqrt{{a}^{\mathrm{4}} +{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{4}} }\right)}\\{{b}\left(\mathrm{1}−\frac{\mathrm{1}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\left({b}^{\mathrm{2}} +\sqrt{{a}^{\mathrm{4}} +{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{4}} }\right)\right)}\end{pmatrix} \\ $$$$\mid{EF}\mid=\mathrm{2}\sqrt{\frac{{a}^{\mathrm{4}} +{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{4}} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$$${a}=\mathrm{3} \\ $$$${b}=\mathrm{2} \\ $$$$\Rightarrow\:\mid{EF}\mid=\mathrm{2}\sqrt{\frac{\mathrm{133}}{\mathrm{13}}}\approx\mathrm{6}.\mathrm{39711} \\ $$
Commented by behi83417@gmail.com last updated on 09/Nov/18
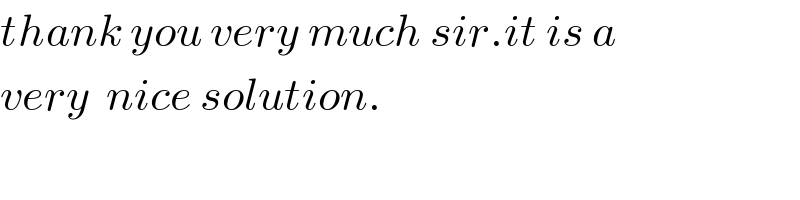
$${thank}\:{you}\:{very}\:{much}\:{sir}.{it}\:{is}\:{a} \\ $$$${very}\:\:{nice}\:{solution}. \\ $$
Answered by behi83417@gmail.com last updated on 09/Nov/18

Answered by mr W last updated on 09/Nov/18

Commented by mr W last updated on 09/Nov/18
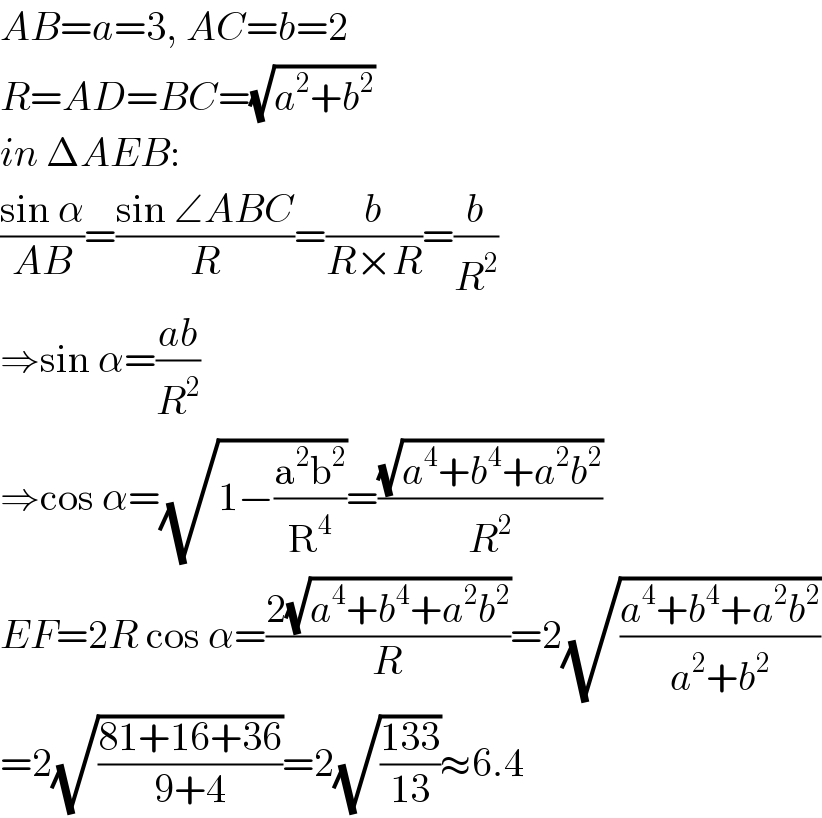
$${AB}={a}=\mathrm{3},\:{AC}={b}=\mathrm{2} \\ $$$${R}={AD}={BC}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$${in}\:\Delta{AEB}: \\ $$$$\frac{\mathrm{sin}\:\alpha}{{AB}}=\frac{\mathrm{sin}\:\angle{ABC}}{{R}}=\frac{{b}}{{R}×{R}}=\frac{{b}}{{R}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{sin}\:\alpha=\frac{{ab}}{{R}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{cos}\:\alpha=\sqrt{\mathrm{1}−\frac{\mathrm{a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} }{\mathrm{R}^{\mathrm{4}} }}=\frac{\sqrt{{a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{a}^{\mathrm{2}} {b}^{\mathrm{2}} }}{{R}^{\mathrm{2}} } \\ $$$${EF}=\mathrm{2}{R}\:\mathrm{cos}\:\alpha=\frac{\mathrm{2}\sqrt{{a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{a}^{\mathrm{2}} {b}^{\mathrm{2}} }}{{R}}=\mathrm{2}\sqrt{\frac{{a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$$$=\mathrm{2}\sqrt{\frac{\mathrm{81}+\mathrm{16}+\mathrm{36}}{\mathrm{9}+\mathrm{4}}}=\mathrm{2}\sqrt{\frac{\mathrm{133}}{\mathrm{13}}}\approx\mathrm{6}.\mathrm{4} \\ $$
Commented by behi83417@gmail.com last updated on 09/Nov/18

$${congratulation}\:{to}\:{new}\:{ID}\:{and}\:{to} \\ $$$${new}\:{smartphone},{dear}\:{master}. \\ $$$${thank}\:{you}\:{for}\:{solving}\:{this}\:{question}. \\ $$
