Question Number 47376 by vajpaithegrate@gmail.com last updated on 09/Nov/18
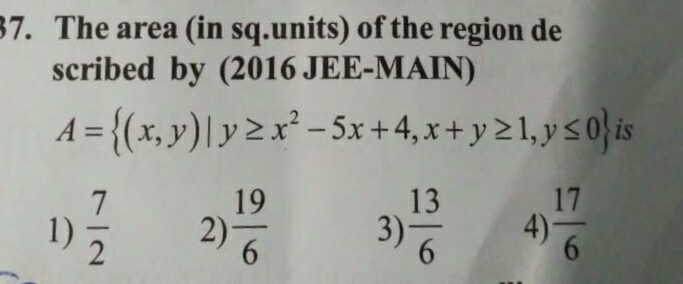
Answered by MJS last updated on 09/Nov/18
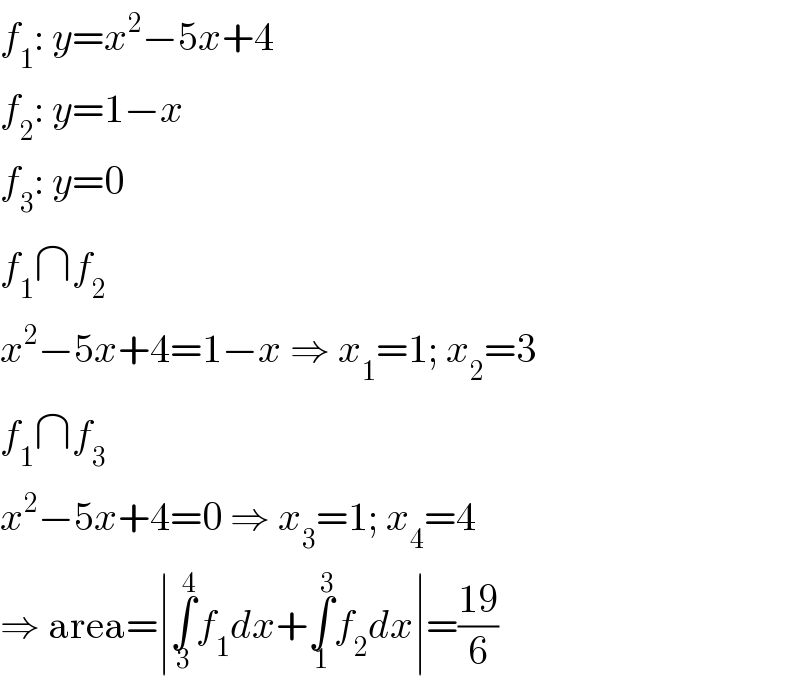
$${f}_{\mathrm{1}} :\:{y}={x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{4} \\ $$$${f}_{\mathrm{2}} :\:{y}=\mathrm{1}−{x} \\ $$$${f}_{\mathrm{3}} :\:{y}=\mathrm{0} \\ $$$${f}_{\mathrm{1}} \cap{f}_{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{4}=\mathrm{1}−{x}\:\Rightarrow\:{x}_{\mathrm{1}} =\mathrm{1};\:{x}_{\mathrm{2}} =\mathrm{3} \\ $$$${f}_{\mathrm{1}} \cap{f}_{\mathrm{3}} \\ $$$${x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{4}=\mathrm{0}\:\Rightarrow\:{x}_{\mathrm{3}} =\mathrm{1};\:{x}_{\mathrm{4}} =\mathrm{4} \\ $$$$\Rightarrow\:\mathrm{area}=\mid\underset{\mathrm{3}} {\overset{\mathrm{4}} {\int}}{f}_{\mathrm{1}} {dx}+\underset{\mathrm{1}} {\overset{\mathrm{3}} {\int}}{f}_{\mathrm{2}} {dx}\mid=\frac{\mathrm{19}}{\mathrm{6}} \\ $$
Commented by vajpaithegrate@gmail.com last updated on 09/Nov/18

$$\mathrm{thank}\:\mathrm{u}\:\mathrm{sir} \\ $$
