Question Number 47402 by Aditya789 last updated on 09/Nov/18

Commented by Aditya789 last updated on 10/Nov/18

$$\mathrm{plz}\:\mathrm{explain} \\ $$
Commented by maxmathsup by imad last updated on 10/Nov/18
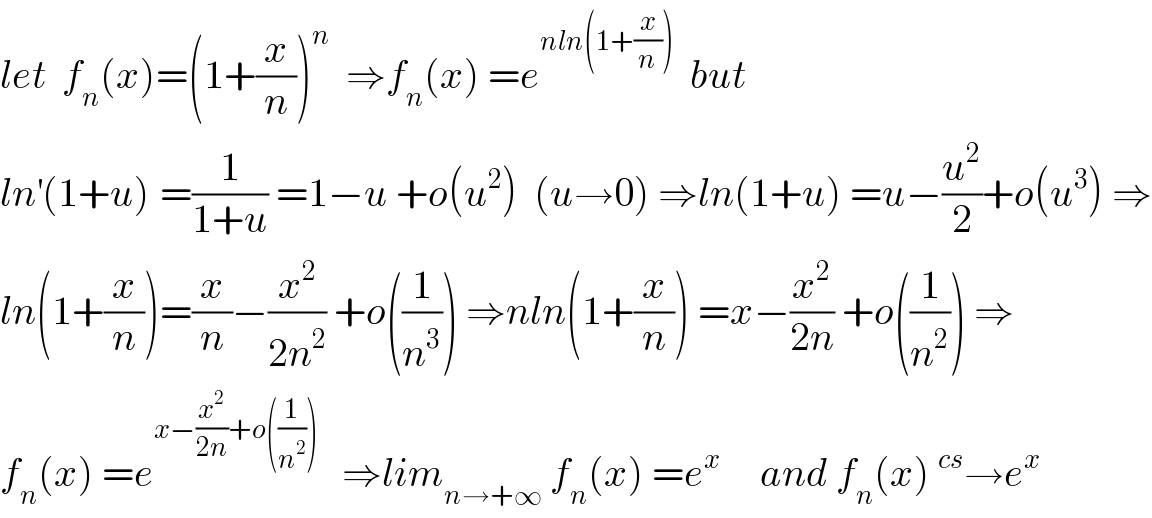
$${let}\:\:{f}_{{n}} \left({x}\right)=\left(\mathrm{1}+\frac{{x}}{{n}}\right)^{{n}} \:\:\Rightarrow{f}_{{n}} \left({x}\right)\:={e}^{{nln}\left(\mathrm{1}+\frac{{x}}{{n}}\right)} \:\:{but} \\ $$$${ln}^{'} \left(\mathrm{1}+{u}\right)^{} =\frac{\mathrm{1}}{\mathrm{1}+{u}}\:=\mathrm{1}−{u}\:+{o}\left({u}^{\mathrm{2}} \right)\:\:\left({u}\rightarrow\mathrm{0}\right)\:\Rightarrow{ln}\left(\mathrm{1}+{u}\right)\:={u}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}+{o}\left({u}^{\mathrm{3}} \right)\:\Rightarrow \\ $$$${ln}\left(\mathrm{1}+\frac{{x}}{{n}}\right)=\frac{{x}}{{n}}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}{n}^{\mathrm{2}} }\:+{o}\left(\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\right)\:\Rightarrow{nln}\left(\mathrm{1}+\frac{{x}}{{n}}\right)\:={x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}{n}}\:+{o}\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)\:\Rightarrow \\ $$$${f}_{{n}} \left({x}\right)\:={e}^{{x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}{n}}+{o}\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)} \:\:\:\Rightarrow{lim}_{{n}\rightarrow+\infty} \:{f}_{{n}} \left({x}\right)\:={e}^{{x}} \:\:\:\:\:{and}\:{f}_{{n}} \left({x}\right)\:^{{cs}} \rightarrow{e}^{{x}} \\ $$
Answered by ajfour last updated on 09/Nov/18
![=lim_(n→∞) {[(1+(x/n))]^(n/x) }^x = e^x .](https://www.tinkutara.com/question/Q47404.png)
$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left\{\left[\left(\mathrm{1}+\frac{{x}}{{n}}\right)\right]^{{n}/{x}} \right\}^{{x}} \:=\:{e}^{{x}} \:. \\ $$
Answered by rahul 19 last updated on 10/Nov/18
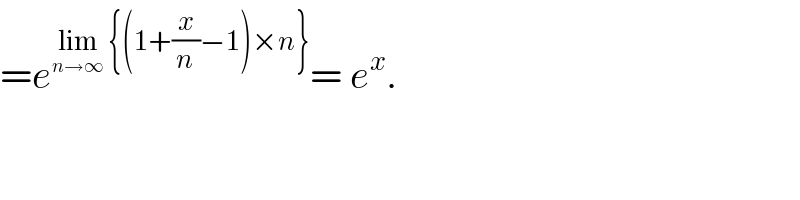
$$={e}^{\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left\{\left(\mathrm{1}+\frac{{x}}{{n}}−\mathrm{1}\right)×{n}\right\}} =\:{e}^{{x}} .\: \\ $$
