Question Number 47497 by MrW3 last updated on 10/Nov/18
Commented by MrW3 last updated on 10/Nov/18

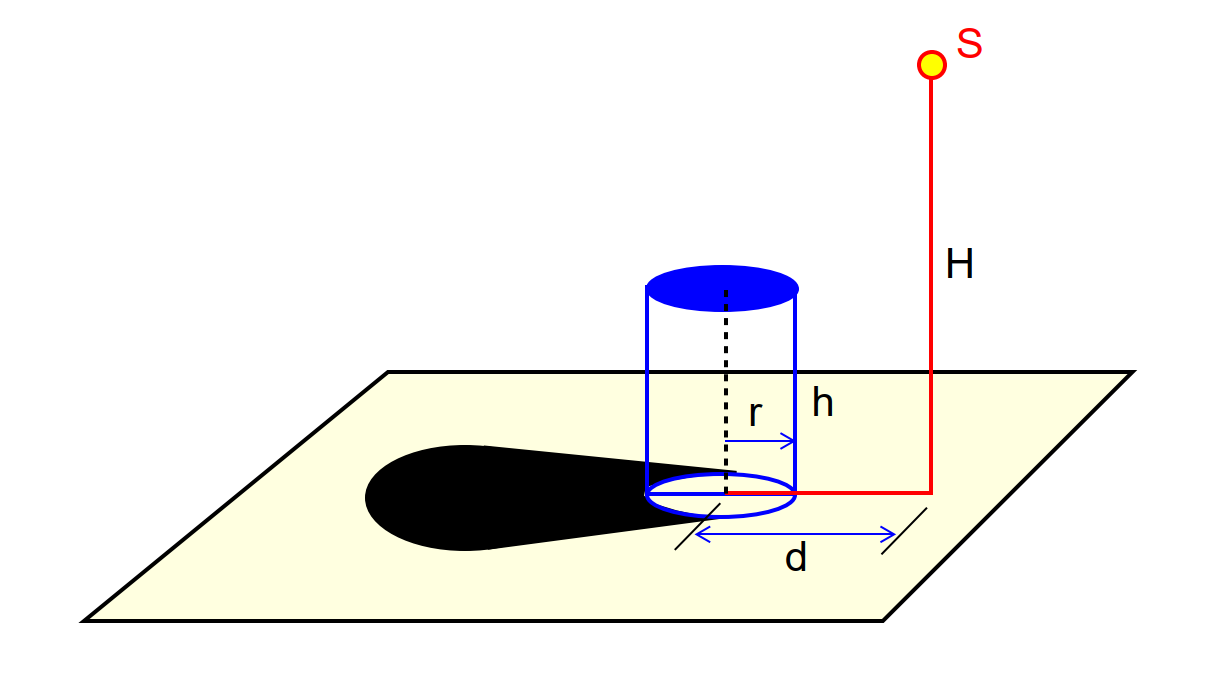
$${Find}\:{the}\:{area}\:{of}\:{the}\:{shadow}\:{of}\:{the} \\ $$$${cylinder}\:{produced}\:{by}\:{a}\:{point}\:{source}\:{of} \\ $$$${light}\:{S}. \\ $$$$ \\ $$$${see}\:{also}\:{Q}\mathrm{47449}. \\ $$
Answered by mr W last updated on 12/Nov/18
Commented by mr W last updated on 12/Nov/18
![If the side wall of the cylinder were transparent, we would only see the shadow of cylinder′s top. Since the top is a circle, it can be easily seen, that its shadow has also the shape of a circle. (L/(d+r))=(H/(H−h)) ⇒L=((H(d+r))/(H−h)) ((2e)/(2r))=(H/(H−h)) ⇒e=((Hr)/(H−h))=b cos θ=(r/d) ⇒θ=cos^(−1) (r/d) A_(shadow) =e(L−e) sin θ+πe^2 −θe^2 −πr^2 A_(shadow) =((Hr)/(H−h))[((H(d+r))/(H−h))−((Hr)/(H−h))]sin θ+(π−cos^(−1) (r/d))((H^2 r^2 )/((H−h)^2 ))−πr^2 ⇒A_(shadow) =((H^2 r)/((H−h)^2 ))[(√(d^2 −r^2 ))+r(π−cos^(−1) (r/d))]−πr^2](https://www.tinkutara.com/question/Q47660.png)
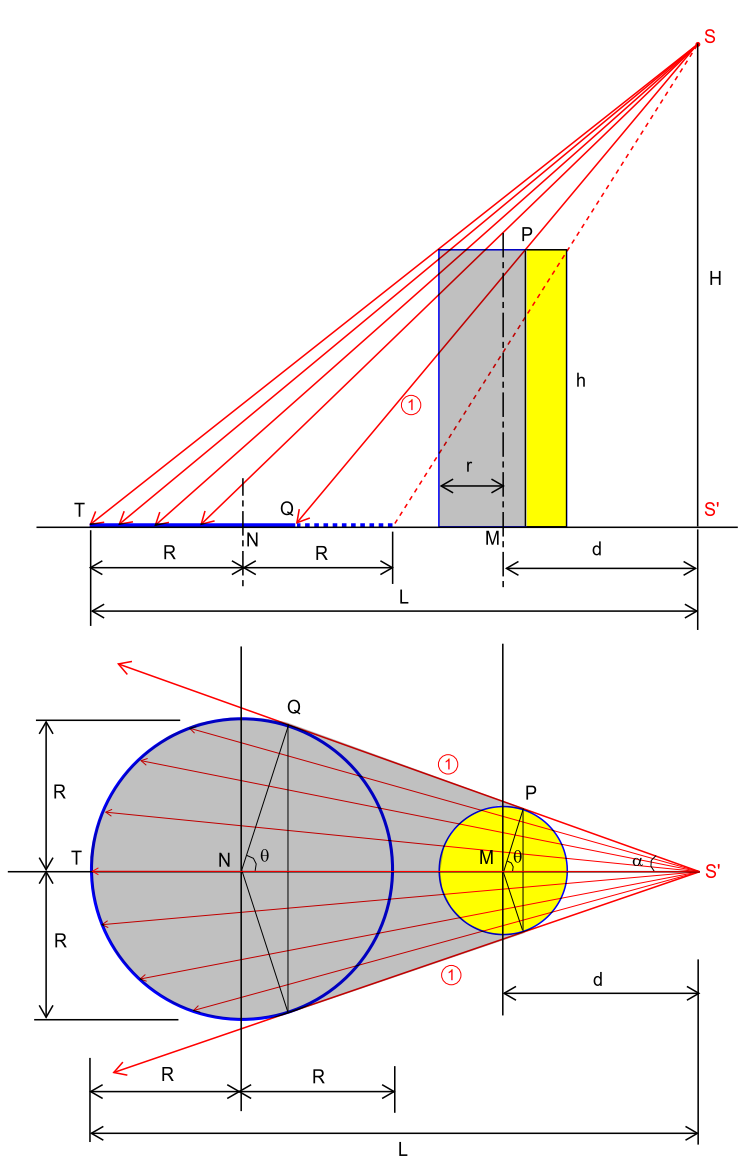
$${If}\:{the}\:{side}\:{wall}\:{of}\:{the}\:{cylinder}\:{were} \\ $$$${transparent},\:{we}\:{would}\:{only}\:{see}\:{the} \\ $$$${shadow}\:{of}\:{cylinder}'{s}\:{top}.\:{Since}\:{the} \\ $$$${top}\:{is}\:{a}\:{circle},\:{it}\:{can}\:{be}\:{easily}\:{seen}, \\ $$$${that}\:{its}\:{shadow}\:{has}\:{also}\:{the}\:{shape}\:{of} \\ $$$${a}\:{circle}. \\ $$$$\frac{{L}}{{d}+{r}}=\frac{{H}}{{H}−{h}} \\ $$$$\Rightarrow{L}=\frac{{H}\left({d}+{r}\right)}{{H}−{h}} \\ $$$$\frac{\mathrm{2}{e}}{\mathrm{2}{r}}=\frac{{H}}{{H}−{h}} \\ $$$$\Rightarrow{e}=\frac{{Hr}}{{H}−{h}}={b} \\ $$$$\mathrm{cos}\:\theta=\frac{{r}}{{d}} \\ $$$$\Rightarrow\theta=\mathrm{cos}^{−\mathrm{1}} \frac{{r}}{{d}} \\ $$$${A}_{{shadow}} ={e}\left({L}−{e}\right)\:\mathrm{sin}\:\theta+\pi{e}^{\mathrm{2}} −\theta{e}^{\mathrm{2}} −\pi{r}^{\mathrm{2}} \\ $$$${A}_{{shadow}} =\frac{{Hr}}{{H}−{h}}\left[\frac{{H}\left({d}+{r}\right)}{{H}−{h}}−\frac{{Hr}}{{H}−{h}}\right]\mathrm{sin}\:\theta+\left(\pi−\mathrm{cos}^{−\mathrm{1}} \frac{{r}}{{d}}\right)\frac{{H}^{\mathrm{2}} {r}^{\mathrm{2}} }{\left({H}−{h}\right)^{\mathrm{2}} }−\pi{r}^{\mathrm{2}} \\ $$$$\Rightarrow{A}_{{shadow}} =\frac{{H}^{\mathrm{2}} {r}}{\left({H}−{h}\right)^{\mathrm{2}} }\left[\sqrt{{d}^{\mathrm{2}} −{r}^{\mathrm{2}} }+{r}\left(\pi−\mathrm{cos}^{−\mathrm{1}} \frac{{r}}{{d}}\right)\right]−\pi{r}^{\mathrm{2}} \\ $$
Commented by ajfour last updated on 14/Nov/18
$${Thank}\:{you}\:{Sir}.\:{I}\:{was}\:{mislead}! \\ $$
