Question Number 47513 by ajfour last updated on 11/Nov/18
Commented by ajfour last updated on 11/Nov/18
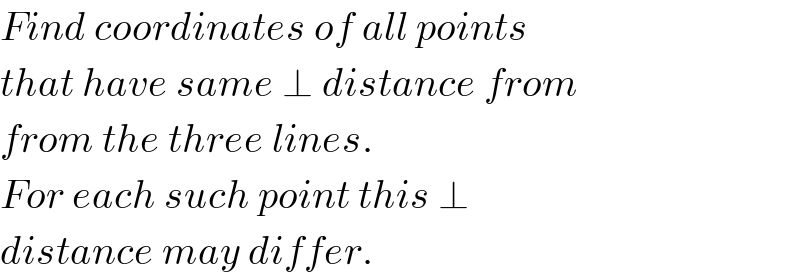
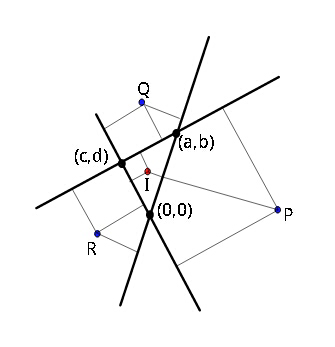
$${Find}\:{coordinates}\:{of}\:{all}\:{points} \\ $$$${that}\:{have}\:{same}\:\bot\:{distance}\:{from} \\ $$$${from}\:{the}\:{three}\:{lines}. \\ $$$${For}\:{each}\:{such}\:{point}\:{this}\:\bot \\ $$$${distance}\:{may}\:{differ}. \\ $$
Answered by mr W last updated on 11/Nov/18
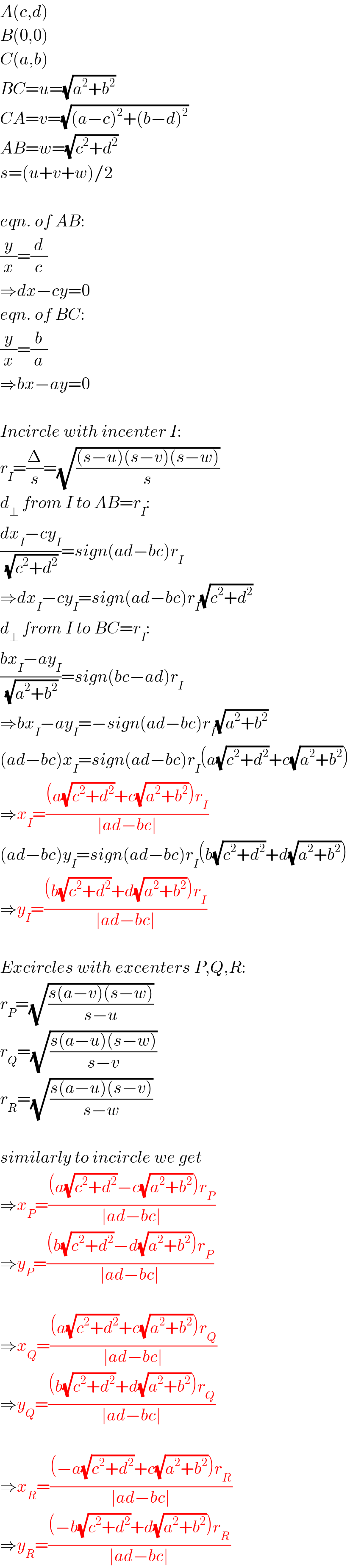
$${A}\left({c},{d}\right) \\ $$$${B}\left(\mathrm{0},\mathrm{0}\right) \\ $$$${C}\left({a},{b}\right) \\ $$$${BC}={u}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$${CA}={v}=\sqrt{\left({a}−{c}\right)^{\mathrm{2}} +\left({b}−{d}\right)^{\mathrm{2}} } \\ $$$${AB}={w}=\sqrt{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} } \\ $$$${s}=\left({u}+{v}+{w}\right)/\mathrm{2} \\ $$$$ \\ $$$${eqn}.\:{of}\:{AB}: \\ $$$$\frac{{y}}{{x}}=\frac{{d}}{{c}} \\ $$$$\Rightarrow{dx}−{cy}=\mathrm{0} \\ $$$${eqn}.\:{of}\:{BC}: \\ $$$$\frac{{y}}{{x}}=\frac{{b}}{{a}} \\ $$$$\Rightarrow{bx}−{ay}=\mathrm{0} \\ $$$$ \\ $$$${Incircle}\:{with}\:{incenter}\:{I}: \\ $$$${r}_{{I}} =\frac{\Delta}{{s}}=\sqrt{\frac{\left({s}−{u}\right)\left({s}−{v}\right)\left({s}−{w}\right)}{{s}}} \\ $$$${d}_{\bot} \:{from}\:{I}\:{to}\:{AB}={r}_{{I}} : \\ $$$$\frac{{dx}_{{I}} −{cy}_{{I}} }{\:\sqrt{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} }}={sign}\left({ad}−{bc}\right){r}_{{I}} \\ $$$$\Rightarrow{dx}_{{I}} −{cy}_{{I}} ={sign}\left({ad}−{bc}\right){r}_{{I}} \sqrt{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} } \\ $$$${d}_{\bot} \:{from}\:{I}\:{to}\:{BC}={r}_{{I}} : \\ $$$$\frac{{bx}_{{I}} −{ay}_{{I}} }{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}={sign}\left({bc}−{ad}\right){r}_{{I}} \\ $$$$\Rightarrow{bx}_{{I}} −{ay}_{{I}} =−{sign}\left({ad}−{bc}\right){r}_{{I}} \sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$\left({ad}−{bc}\right){x}_{{I}} ={sign}\left({ad}−{bc}\right){r}_{{I}} \left({a}\sqrt{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} }+{c}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow{x}_{{I}} =\frac{\left({a}\sqrt{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} }+{c}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right){r}_{{I}} }{\mid{ad}−{bc}\mid} \\ $$$$\left({ad}−{bc}\right){y}_{{I}} ={sign}\left({ad}−{bc}\right){r}_{{I}} \left({b}\sqrt{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} }+{d}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow{y}_{{I}} =\frac{\left({b}\sqrt{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} }+{d}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right){r}_{{I}} }{\mid{ad}−{bc}\mid} \\ $$$$ \\ $$$${Excircles}\:{with}\:{excenters}\:{P},{Q},{R}: \\ $$$${r}_{{P}} =\sqrt{\frac{{s}\left({a}−{v}\right)\left({s}−{w}\right)}{{s}−{u}}} \\ $$$${r}_{{Q}} =\sqrt{\frac{{s}\left({a}−{u}\right)\left({s}−{w}\right)}{{s}−{v}}} \\ $$$${r}_{{R}} =\sqrt{\frac{{s}\left({a}−{u}\right)\left({s}−{v}\right)}{{s}−{w}}} \\ $$$$ \\ $$$${similarly}\:{to}\:{incircle}\:{we}\:{get} \\ $$$$\Rightarrow{x}_{{P}} =\frac{\left({a}\sqrt{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} }−{c}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right){r}_{{P}} }{\mid{ad}−{bc}\mid} \\ $$$$\Rightarrow{y}_{{P}} =\frac{\left({b}\sqrt{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} }−{d}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right){r}_{{P}} }{\mid{ad}−{bc}\mid} \\ $$$$ \\ $$$$\Rightarrow{x}_{{Q}} =\frac{\left({a}\sqrt{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} }+{c}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right){r}_{{Q}} }{\mid{ad}−{bc}\mid} \\ $$$$\Rightarrow{y}_{{Q}} =\frac{\left({b}\sqrt{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} }+{d}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right){r}_{{Q}} }{\mid{ad}−{bc}\mid} \\ $$$$ \\ $$$$\Rightarrow{x}_{{R}} =\frac{\left(−{a}\sqrt{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} }+{c}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right){r}_{{R}} }{\mid{ad}−{bc}\mid} \\ $$$$\Rightarrow{y}_{{R}} =\frac{\left(−{b}\sqrt{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} }+{d}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right){r}_{{R}} }{\mid{ad}−{bc}\mid} \\ $$
Commented by ajfour last updated on 11/Nov/18

$${Excellent}\:{Sir}. \\ $$$${beautiful}\:{results}. \\ $$
Commented by peter frank last updated on 11/Nov/18
$$\mathrm{what}\:\mathrm{app}\:\mathrm{do}\:\mathrm{you}\:\mathrm{use}\:\mathrm{sir}? \\ $$
Commented by mr W last updated on 11/Nov/18
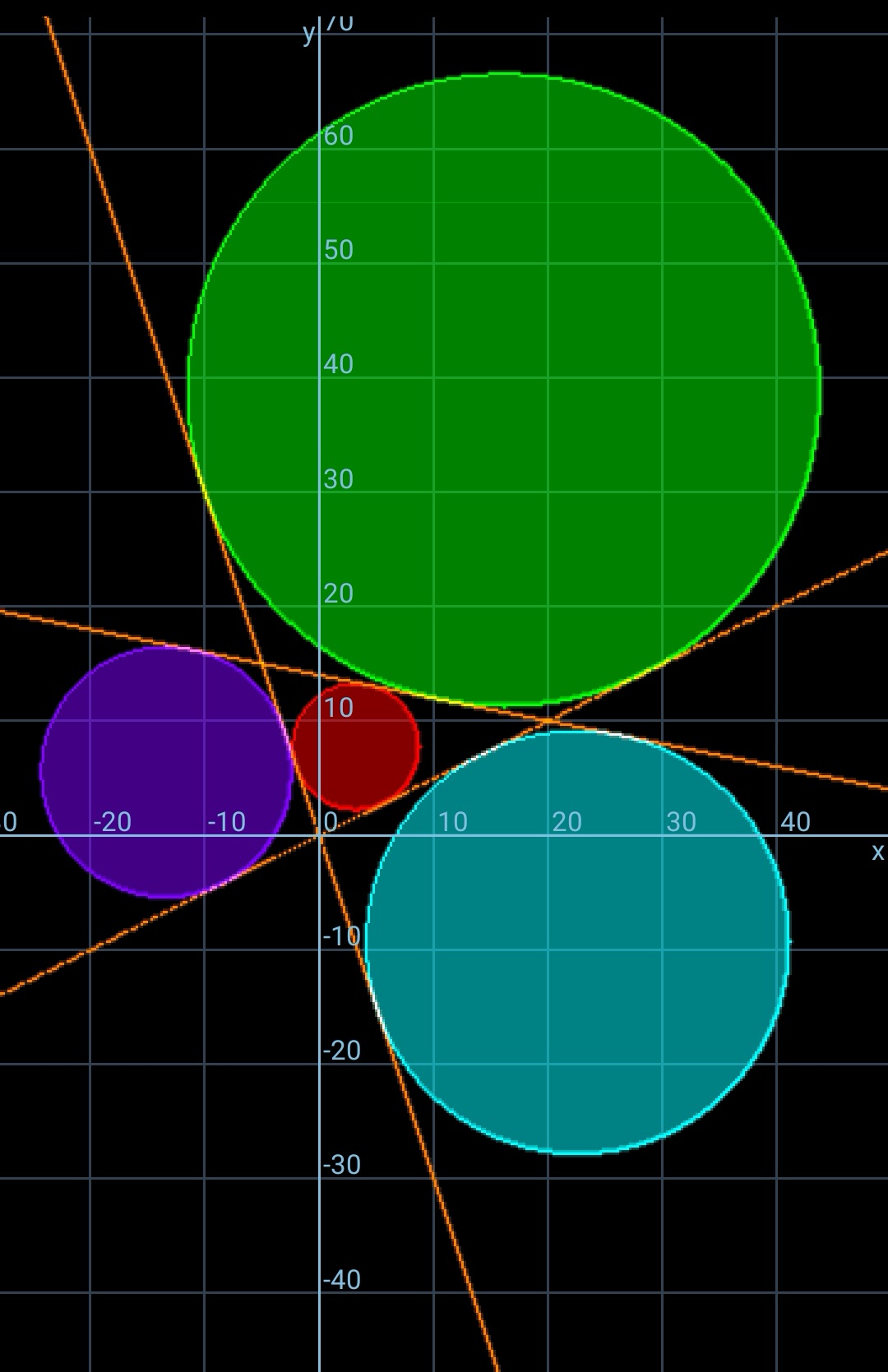
Commented by mr W last updated on 11/Nov/18
$${to}\:{draw}\:{the}\:{graph}\:{I}\:{used}\:{the}\:{app}\:{Grapher}. \\ $$
