Question Number 47531 by peter frank last updated on 11/Nov/18
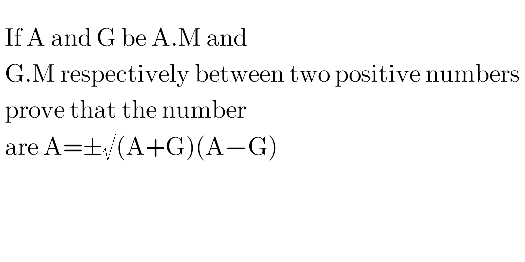
Commented by math1967 last updated on 11/Nov/18
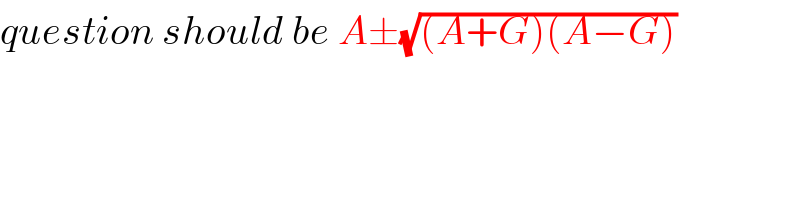
$${question}\:{should}\:{be}\:{A}\pm\sqrt{\left({A}+{G}\right)\left({A}−{G}\right)} \\ $$
Commented by peter frank last updated on 11/Nov/18
$$\mathrm{yes}\:\mathrm{sir}.\mathrm{thanks}\:\mathrm{for}\:\mathrm{correction} \\ $$
Answered by math1967 last updated on 11/Nov/18
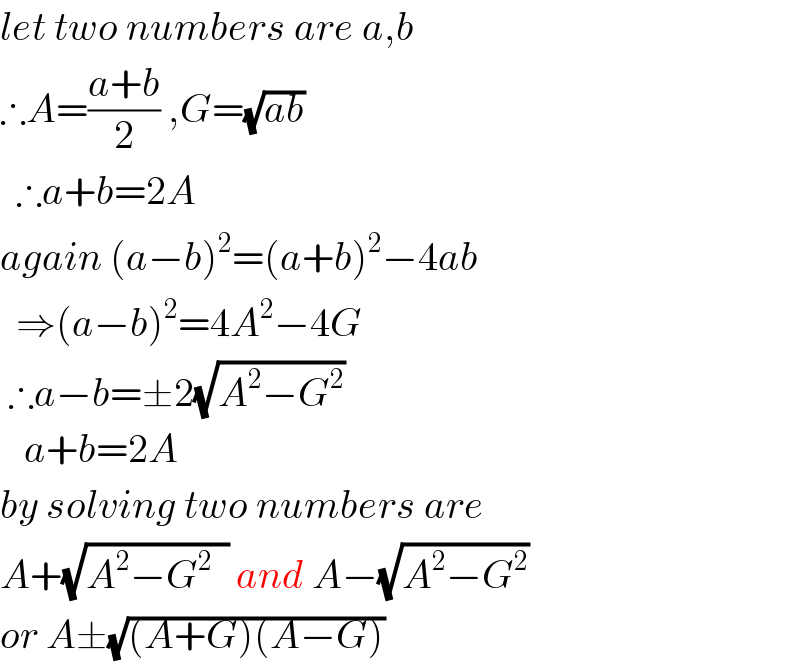
$${let}\:{two}\:{numbers}\:{are}\:{a},{b} \\ $$$$\therefore{A}=\frac{{a}+{b}}{\mathrm{2}}\:,{G}=\sqrt{{ab}}\: \\ $$$$\:\:\therefore{a}+{b}=\mathrm{2}{A}\: \\ $$$${again}\:\left({a}−{b}\right)^{\mathrm{2}} =\left({a}+{b}\right)^{\mathrm{2}} −\mathrm{4}{ab} \\ $$$$\:\:\Rightarrow\left({a}−{b}\right)^{\mathrm{2}} =\mathrm{4}{A}^{\mathrm{2}} −\mathrm{4}{G} \\ $$$$\:\therefore{a}−{b}=\pm\mathrm{2}\sqrt{{A}^{\mathrm{2}} −{G}^{\mathrm{2}} } \\ $$$$\:\:\:{a}+{b}=\mathrm{2}{A} \\ $$$${by}\:{solving}\:{two}\:{numbers}\:{are} \\ $$$${A}+\sqrt{{A}^{\mathrm{2}} −{G}^{\mathrm{2}} \:\:}\:{and}\:{A}−\sqrt{{A}^{\mathrm{2}} −{G}^{\mathrm{2}} } \\ $$$${or}\:{A}\pm\sqrt{\left({A}+{G}\right)\left({A}−{G}\right)} \\ $$
