Question Number 47824 by ajfour last updated on 15/Nov/18
Commented by ajfour last updated on 15/Nov/18

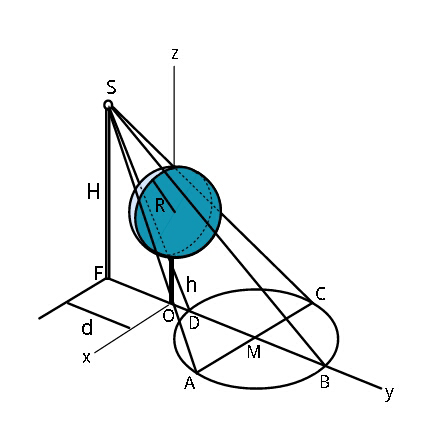
$${Find}\:{the}\:{equation}\:{of}\:{the}\:{shadow} \\ $$$${curve}\:{of}\:{a}\:{sphere}\:{of}\:{radius}\:{R} \\ $$$${mounted}\:{on}\:{a}\:{pole}\:{of}\:{height}\:{h}. \\ $$
Commented by ajfour last updated on 15/Nov/18
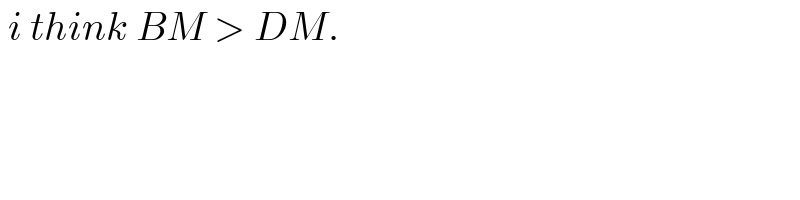
$$\:{i}\:{think}\:{BM}\:>\:{DM}. \\ $$
Answered by ajfour last updated on 16/Nov/18
![S(0,−d,H) ; let E be center of sphere: E(0,0,h+R)≡(0,0,z_0 ) let a ray grazing the sphere hit the shadow-curve boundary at (p,q). Eq. of such a ray: r^� =−dj^� +Hk^� +λ(pi^� +(q+d)j^� −Hk^� ) ⊥ distance of v^� from a line r^� =a^� +λb^� , we need to obtain this first. _________________________ let foot of ⊥ from v^� to line be r^� = a^� +λ_0 b^� ⇒ (a^� +λ_0 b^� −v^� ).b^� = 0 ⇒ λ_0 =(((v^� −a^� ).b^� )/(b^� .b^� )) hence ⊥ distance is d = ∣a^� +λ_0 b^� −v^� ∣ = ∣a^� −v^� +((((v^� −a^� ).b^� )/(b^� .b^� )))b^� ∣ ________________________ Now ⊥ distance of ray from center of sphere E is R. So ∣−dj^� +Hk^� +(([dj^� +(h+R−H)k^� ].[pi^� +(q+d)j^� −Hk^� ](pi^� +(q+d)j^� −Hk^� ])/(p^2 +(q+d)^2 +H^2 ))−(h+R)k^� ∣=R ∣−dj^� +Hk^� +(([d(y+d)−H(h+R−H)](xi^� +(y+d)j^� −Hk^� ])/(x^2 +(y+d)^2 +H^2 ))−(h+R)k^� ∣=R _________________________.](https://www.tinkutara.com/question/Q47833.png)
$${S}\left(\mathrm{0},−{d},{H}\right)\:\:;\:{let}\:{E}\:{be}\:{center}\:{of} \\ $$$${sphere}:\:\:\:{E}\left(\mathrm{0},\mathrm{0},{h}+{R}\right)\equiv\left(\mathrm{0},\mathrm{0},{z}_{\mathrm{0}} \right) \\ $$$${let}\:{a}\:{ray}\:{grazing}\:{the}\:{sphere}\:{hit} \\ $$$${the}\:{shadow}-{curve}\:{boundary}\:{at} \\ $$$$\left({p},{q}\right). \\ $$$${Eq}.\:{of}\:{such}\:{a}\:{ray}: \\ $$$$\bar {{r}}=−{d}\hat {{j}}+{H}\hat {{k}}+\lambda\left({p}\hat {{i}}+\left({q}+{d}\right)\hat {{j}}−{H}\hat {{k}}\right) \\ $$$$\bot\:{distance}\:{of}\:\bar {{v}}\:{from}\:{a}\:{line} \\ $$$$\:\:\bar {{r}}\:=\bar {{a}}+\lambda\bar {{b}}\:,\:{we}\:{need}\:{to}\:{obtain}\:{this} \\ $$$${first}. \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${let}\:{foot}\:{of}\:\bot\:{from}\:\bar {{v}}\:{to}\:{line}\:{be} \\ $$$$\:\:\bar {{r}}\:=\:\bar {{a}}+\lambda_{\mathrm{0}} \bar {{b}} \\ $$$$\Rightarrow\:\:\left(\bar {{a}}+\lambda_{\mathrm{0}} \bar {{b}}−\bar {{v}}\right).\bar {{b}}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\:\lambda_{\mathrm{0}} =\frac{\left(\bar {{v}}−\bar {{a}}\right).\bar {{b}}}{\bar {{b}}.\bar {{b}}} \\ $$$${hence}\:\bot\:{distance}\:{is}\: \\ $$$$\:\:\:\:\:{d}\:=\:\mid\bar {{a}}+\lambda_{\mathrm{0}} \bar {{b}}−\bar {{v}}\mid \\ $$$$\:\:\:\:\:\:\:\:=\:\mid\bar {{a}}−\bar {{v}}+\left(\frac{\left(\bar {{v}}−\bar {{a}}\right).\bar {{b}}}{\bar {{b}}.\bar {{b}}}\right)\bar {{b}}\mid \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${Now}\:\bot\:{distance}\:{of}\:{ray}\:{from} \\ $$$${center}\:{of}\:{sphere}\:{E}\:{is}\:{R}.\:{So} \\ $$$$\:\mid−{d}\hat {{j}}+{H}\hat {{k}}+\frac{\left[{d}\hat {{j}}+\left({h}+{R}−{H}\right)\hat {{k}}\right].\left[{p}\hat {{i}}+\left({q}+{d}\right)\hat {{j}}−{H}\hat {{k}}\right]\left({p}\hat {{i}}+\left({q}+{d}\right)\hat {{j}}−{H}\hat {{k}}\right]}{{p}^{\mathrm{2}} +\left({q}+{d}\right)^{\mathrm{2}} +{H}^{\mathrm{2}} }−\left({h}+{R}\right)\hat {{k}}\mid={R} \\ $$$$\mid−{d}\hat {{j}}+{H}\hat {{k}}+\frac{\left[{d}\left({y}+{d}\right)−{H}\left({h}+{R}−{H}\right)\right]\left({x}\hat {{i}}+\left({y}+{d}\right)\hat {{j}}−{H}\hat {{k}}\right]}{{x}^{\mathrm{2}} +\left({y}+{d}\right)^{\mathrm{2}} +{H}^{\mathrm{2}} }−\left({h}+{R}\right)\hat {{k}}\mid={R} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_. \\ $$
Commented by ajfour last updated on 15/Nov/18

$${MrW}\:{Sir},\:{any}\:{polar}\:{method}\:{to} \\ $$$${solve}\:{this}\:{question}\:? \\ $$
Answered by mr W last updated on 15/Nov/18
Commented by Tawa1 last updated on 16/Nov/18
$$\mathrm{Sir},\:\mathrm{Do}\:\mathrm{you}\:\mathrm{use}\:\mathrm{Lekh}\:\mathrm{diagram}\:\mathrm{to}\:\mathrm{draw}\:\mathrm{this}\:\mathrm{or}\:\mathrm{another}\:\mathrm{app}.\: \\ $$
Commented by mr W last updated on 16/Nov/18

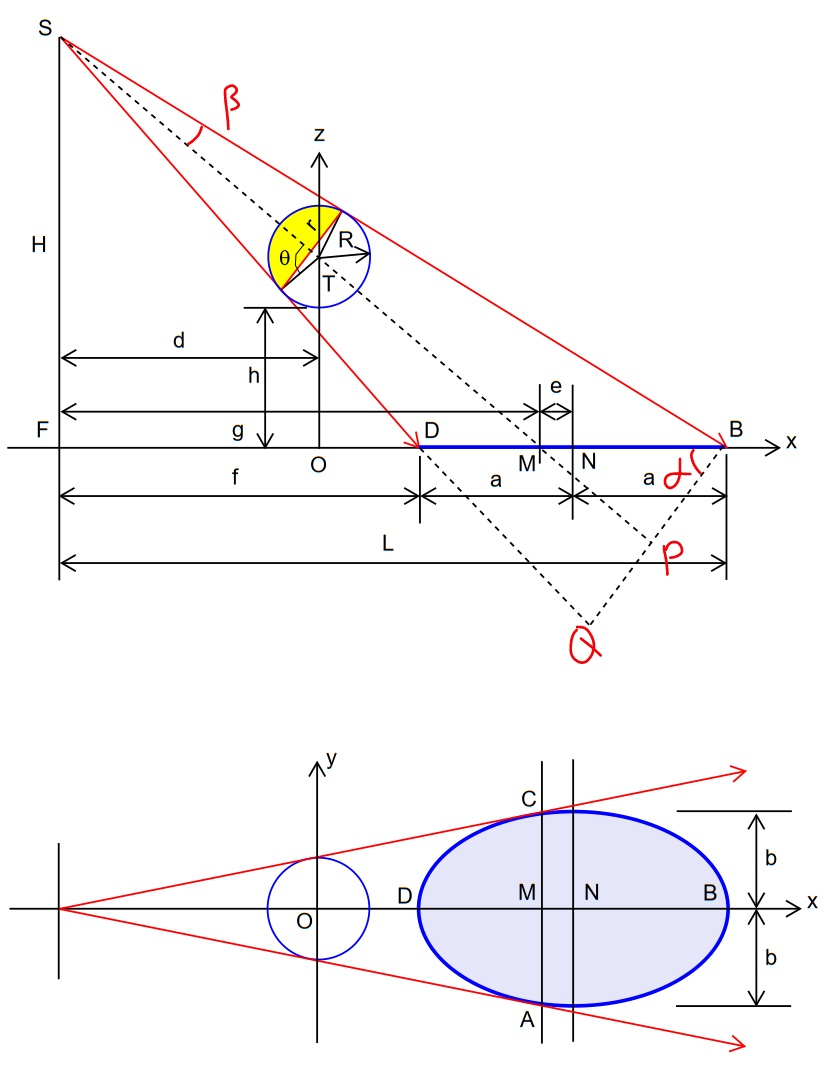
$${Due}\:{to}\:{the}\:{problem}\:{with}\:{my}\:{new}\: \\ $$$${smartphone}\:{I}\:{won}'{t}\:{be}\:{able}\:{to}\:{type} \\ $$$${the}\:{complete}\:{solution}.\:{I}\:{just}\:{can}\:{not} \\ $$$${use}\:{the}\:{app}\:{to}\:{edit}\:{formulas}\:{because} \\ $$$${the}\:{last}\:{row}\:{of}\:{the}\:{menu}\:{is}\:{not}\:{available}. \\ $$$${I}\:{hope}\:{TinkuTara}\:{could}\:{help}\:{me}\:{soon} \\ $$$${to}\:{solve}\:{this}\:{problem}. \\ $$$$ \\ $$$${My}\:{solution}\:{is}\:{quite}\:{easy}.\:{It}\:{uses}\:{that} \\ $$$${what}\:{we}\:{already}\:{know}\:{from}\:\:{Q}\mathrm{44017}. \\ $$$$ \\ $$$${The}\:{shadow}\:{of}\:{the}\:{sphere}\:{on}\:{the}\:{ground} \\ $$$${is}\:{an}\:{oblique}\:{section}\:{of}\:{the}\:{right}\:{cone} \\ $$$${S}−{BPQ}.\:{From}\:{Q}\mathrm{44017}\:{we}\:{know}\:{that}\:{it}'{s} \\ $$$${an}\:{ellipse}.\:{The}\:{parameters}\:{a},{b}\:{for}\:{this} \\ $$$${ellipse}\:{can}\:{be}\:{calculated}\:{with}\:{the} \\ $$$${formulas}\:{for}\:{a}\:{and}\:{b}\:{in}\:{Q}\mathrm{44017}.\:{When} \\ $$$${we}\:{have}\:{them},\:{the}\:{rest}\:{is}\:{clear}. \\ $$
Commented by ajfour last updated on 16/Nov/18
$${Thanks}\:{for}\:{the}\:{diagrams},\:{Sir}. \\ $$$${I}'{ll}\:{try}\:{to}\:{obtain}\:{the}\:{equation} \\ $$$${this}\:{way}. \\ $$
Commented by ajfour last updated on 16/Nov/18

$$\:\:\:\:\underset{−} {{Kindly}\:{allow}\:{a}\:{doubt}} \\ $$$${I}\:{doubt}\:{if}\:{its}\:{an}\:{ellipse}; \\ $$$${corresponding}\:{to}\:{center}\:{of} \\ $$$${object}\:{center},\:{M}\:{is}\:{the}\:{shadow} \\ $$$${center};\:{and}\:{since}\:{projection}\:{of} \\ $$$${QP}\:{on}\:{ground}\:{isDM}\:\left({less}\right. \\ $$$$\left.{magnified}\right)\:\:,\:{while}\:{projection} \\ $$$${of}\:{BP}\:{becomes}\:{BM}\left({magnified}\right. \\ $$$$\left.{more}\right)\:,\:{so}\:{the}\:{two}\:{semi}-{major} \\ $$$${axis}\:{parts},\:\:{DM}\:{and}\:{MB}\:{get} \\ $$$${unequal},\:{M}\:{still}\:{being}\:{the}\:{center} \\ $$$${of}\:{shadow}\:\left({not}\:{a}\:{proper}\:{ellipse}\right). \\ $$
Commented by ajfour last updated on 16/Nov/18
$${I}\:{use}\:{Lekh}\:{Diagram}\:{only}. \\ $$
Commented by Tawa1 last updated on 16/Nov/18
$$\mathrm{Thanks}\:\mathrm{sir}.\:\:\mathrm{I}\:\mathrm{mean}\:\mathrm{sir}\:\mathrm{mrW}\:\mathrm{diagram} \\ $$
Commented by mr W last updated on 16/Nov/18

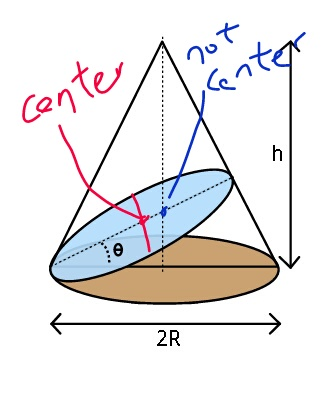
$${ajfour}\:{sir}: \\ $$$${M}\:{is}\:{the}\:{shadow}\:{of}\:{the}\:{center}\:{of}\:{the} \\ $$$${sphere},\:{but}\:{it}\:{is}\:{not}\:{the}\:{center}\:{of}\:{the} \\ $$$${shadow}.\:{DM}<{MB}\:{is}\:{correct}. \\ $$$${the}\:{center}\:{of}\:{the}\:{shadow}\:{is}\:{point}\:{N}, \\ $$$${it}\:{is}\:{there}\:{where}\:{the}\:{shadow}\:{widest}. \\ $$$${since}\:{the}\:{shadow}\:{is}\:{an}\:{oblique}\:{section} \\ $$$${of}\:{a}\:{cone},\:{so}\:{it}\:{is}\:{an}\:{ellipse}.\:{this}\:{is} \\ $$$${sure}. \\ $$
Commented by mr W last updated on 16/Nov/18

$${to}\:{tawa}\mathrm{1}\:{sir}: \\ $$$${I}\:{don}'{t}\:{use}\:{a}\:{special}\:{app}\:{to}\:{draw}\:{my} \\ $$$${diagrams}.\:{Sometimes}\:{I}\:{draw}\:{them} \\ $$$${as}\:{comments}\:{in}\:{a}\:{pdf}\:{document}\:{and} \\ $$$${make}\:{screen}\:{captures}\:{from}\:{them}. \\ $$
Commented by mr W last updated on 16/Nov/18
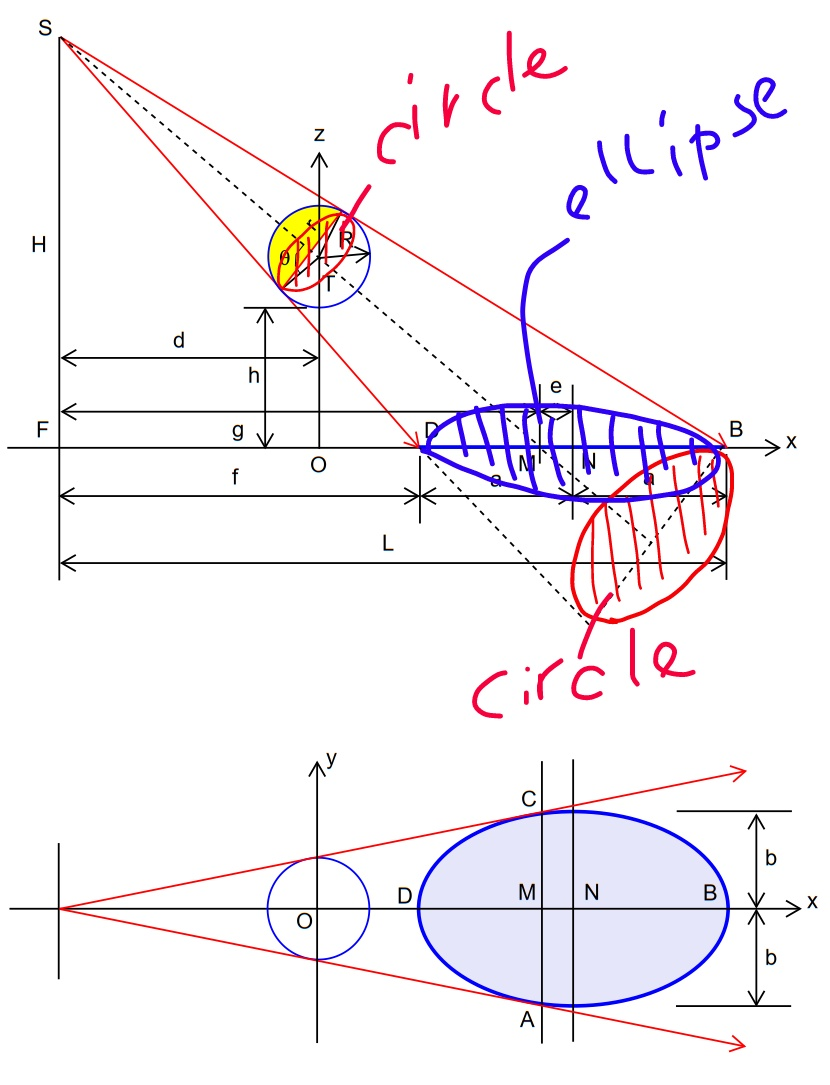
Commented by Tawa1 last updated on 16/Nov/18
$$\mathrm{Alright}\:\mathrm{sir}.\:\mathrm{Thanks}.\: \\ $$
Commented by mr W last updated on 16/Nov/18
Commented by ajfour last updated on 16/Nov/18
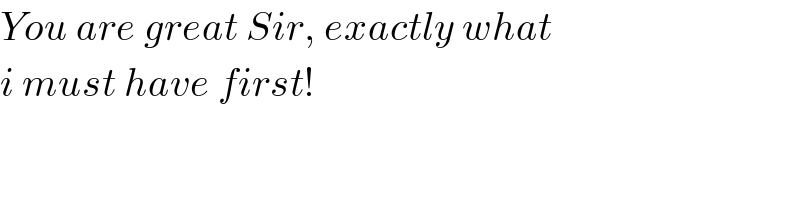
$${You}\:{are}\:{great}\:{Sir},\:{exactly}\:{what} \\ $$$${i}\:{must}\:{have}\:{first}! \\ $$
