Question Number 47831 by somil last updated on 15/Nov/18
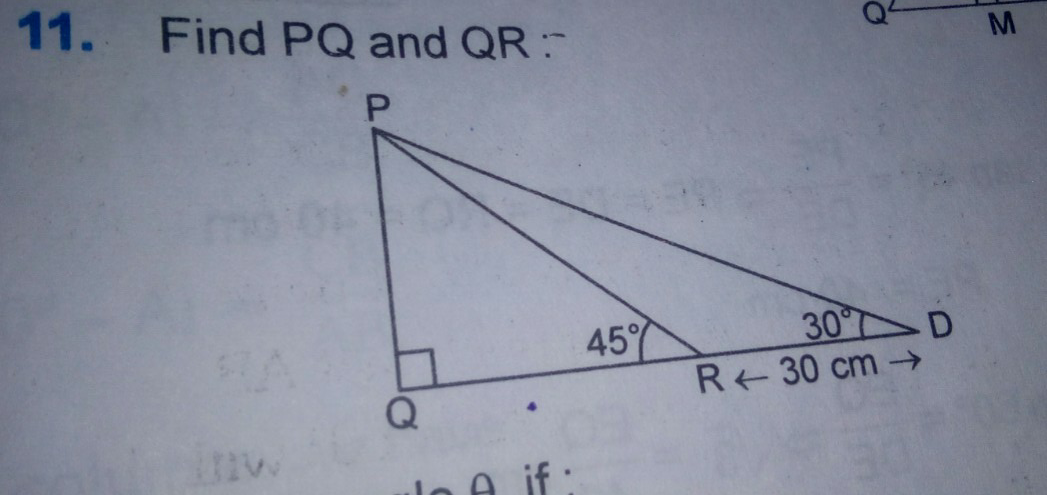
Commented by somil last updated on 16/Nov/18

$${i}\:{know}\: \\ $$
Answered by $@ty@m last updated on 15/Nov/18
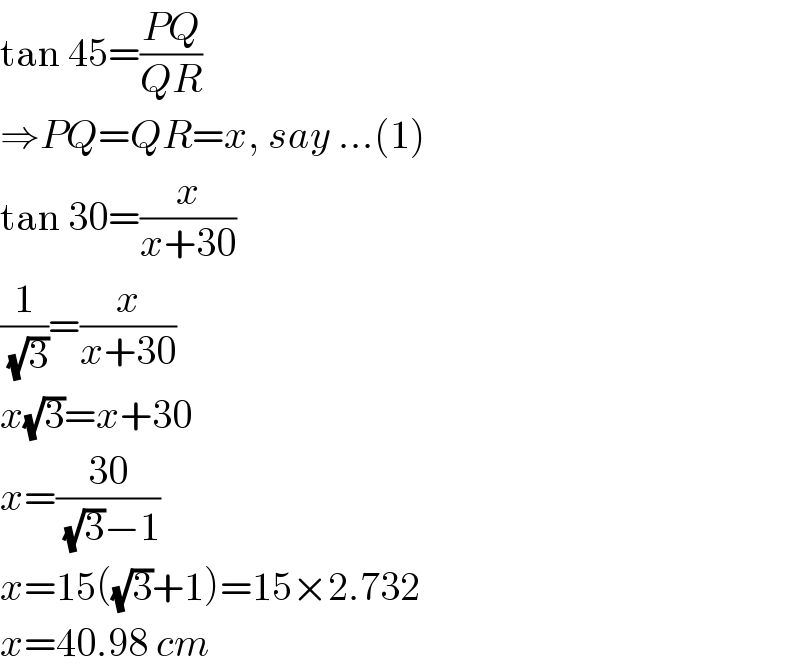
$$\mathrm{tan}\:\mathrm{45}=\frac{{PQ}}{{QR}} \\ $$$$\Rightarrow{PQ}={QR}={x},\:{say}\:…\left(\mathrm{1}\right) \\ $$$$\mathrm{tan}\:\mathrm{30}=\frac{{x}}{{x}+\mathrm{30}} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}=\frac{{x}}{{x}+\mathrm{30}} \\ $$$${x}\sqrt{\mathrm{3}}={x}+\mathrm{30} \\ $$$${x}=\frac{\mathrm{30}}{\:\sqrt{\mathrm{3}}−\mathrm{1}} \\ $$$${x}=\mathrm{15}\left(\sqrt{\mathrm{3}}+\mathrm{1}\right)=\mathrm{15}×\mathrm{2}.\mathrm{732} \\ $$$${x}=\mathrm{40}.\mathrm{98}\:{cm} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 15/Nov/18
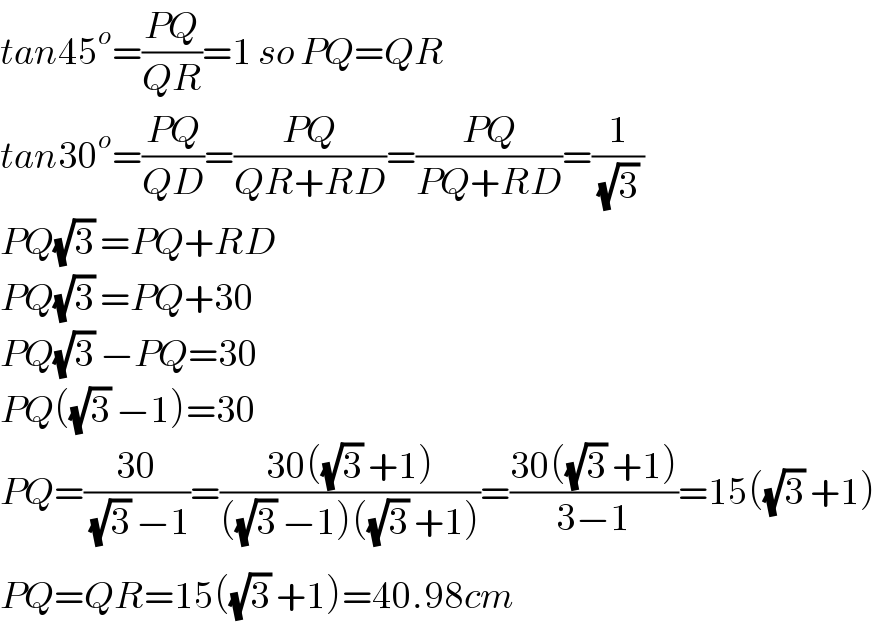
$${tan}\mathrm{45}^{{o}} =\frac{{PQ}}{{QR}}=\mathrm{1}\:{so}\:{PQ}={QR} \\ $$$${tan}\mathrm{30}^{{o}} =\frac{{PQ}}{{QD}}=\frac{{PQ}}{{QR}+{RD}}=\frac{{PQ}}{{PQ}+{RD}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}\:} \\ $$$${PQ}\sqrt{\mathrm{3}}\:={PQ}+{RD} \\ $$$${PQ}\sqrt{\mathrm{3}}\:={PQ}+\mathrm{30} \\ $$$${PQ}\sqrt{\mathrm{3}}\:−{PQ}=\mathrm{30} \\ $$$${PQ}\left(\sqrt{\mathrm{3}}\:−\mathrm{1}\right)=\mathrm{30} \\ $$$${PQ}=\frac{\mathrm{30}}{\:\sqrt{\mathrm{3}}\:−\mathrm{1}}=\frac{\mathrm{30}\left(\sqrt{\mathrm{3}}\:+\mathrm{1}\right)}{\left(\sqrt{\mathrm{3}}\:−\mathrm{1}\right)\left(\sqrt{\mathrm{3}}\:+\mathrm{1}\right)}=\frac{\mathrm{30}\left(\sqrt{\mathrm{3}}\:+\mathrm{1}\right)}{\mathrm{3}−\mathrm{1}}=\mathrm{15}\left(\sqrt{\mathrm{3}}\:+\mathrm{1}\right) \\ $$$${P}\overset{} {{Q}}={QR}=\mathrm{15}\left(\sqrt{\mathrm{3}}\:+\mathrm{1}\right)=\mathrm{40}.\mathrm{98}{cm} \\ $$
