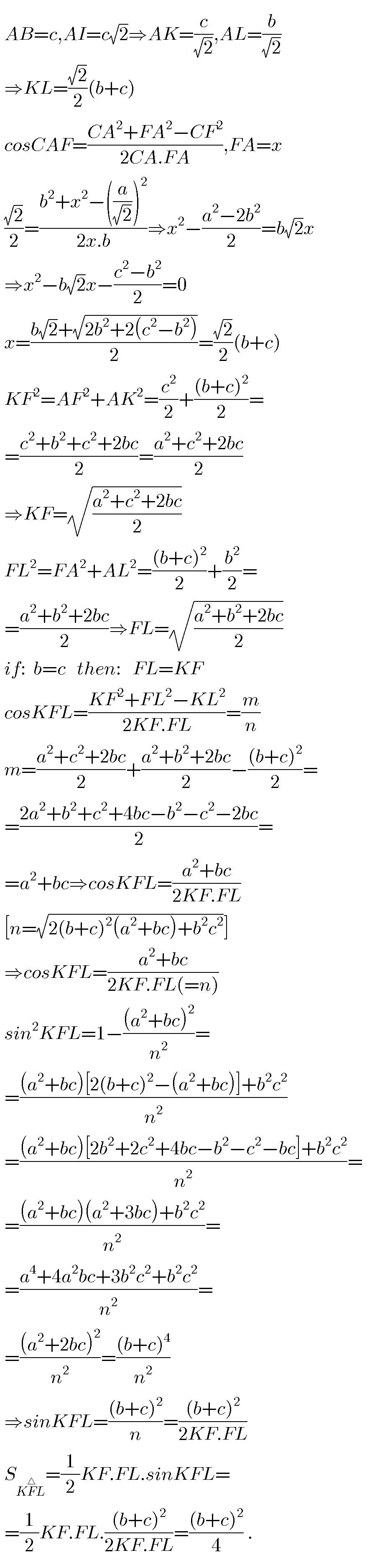Question Number 47883 by behi83417@gmail.com last updated on 16/Nov/18

Commented by behi83417@gmail.com last updated on 16/Nov/18

$$\measuredangle{A}=\mathrm{90}^{\bullet} ,{colored}\:{shapes}\:{such}:{ACHG}, \\ $$$${are}\:{squares}\:{and}\:{points}:{L},…{are} \\ $$$${square}\:{centers}. \\ $$$$\mathrm{1}.{show}\:{that}:\:{AF}\:{is}\:{the}\:{angular}\: \\ $$$${bisector}\:{of}\:\measuredangle{BAC}. \\ $$$$\mathrm{2}.{is}\:{statement}#\mathrm{1}\:{true}\:{for}\:{BL}\:{and}\:{CK}? \\ $$$$\mathrm{3}.{show}\:{that},{F}\overset{\bigtriangleup} {{K}L}\:{is}\:{isoscale}\:{when} \\ $$$${A}\overset{\bigtriangleup} {{B}C}\:{is}\:{isoscale}. \\ $$$$\mathrm{4}.{area}\:{of}\:{F}\overset{\bigtriangleup} {{K}L}\:{in}\:{terms}\:{of}\::\boldsymbol{{a}},\boldsymbol{{b}},\boldsymbol{{c}}. \\ $$$$\left({a},{b},{c}:\:{sides}\:{of}\:{A}\overset{\bigtriangleup} {{B}C}\right). \\ $$
Answered by behi83417@gmail.com last updated on 16/Nov/18
![#1. a circle passing from:A,B,C,also passes from F.because of: ∡BAC=∡BFC=90^• .BF=FC=(a/( (√2))) so BF^(arc) =F^(arc) C⇒BA^� F=CA^� F.so AF,is bisector of BA^� C. or another way: FA=x cosFA^� B=((FA^2 +AB^2 −FB^2 )/(2FA.AB))= =((x^2 +c^2 −((a/( (√2))))^2 )/(2xc))=((2x^2 +2c^2 −b^2 −c^2 )/(4xc))= =((2x^2 +c^2 −b^2 )/(4xc)) (i) cosFA^� C=((FA^2 +AC^2 −FC^2 )/(2FA.AC))= =((x^2 +b^2 −((a/( (√2))))^2 )/(2xb))=((2x^2 +b^2 −c^2 )/(4xb)) (ii) (i)−(ii)=((b(2x^2 +c^2 −b^2 )−c(2x^2 +b^2 −c^2 ))/(4xbc))= =((2x^2 (b−c)−(b^3 −c^3 −bc^2 +cb^2 ))/(4xbc))= =(((b−c)(2x^2 −(b^2 +c^2 +bc)−bc))/(4xbc))= =(((b−c)(2x^2 −(b+c)^2 ))/(4xbc))=0 ⇒∡FAB=∡FAC⇒AF,is bisector. [ABCF,is cyclic.so: x.a=(a/( (√2))).b+(a/( (√2))).c⇒x=((b+c)/( (√2)))] #2. the answer is :no. S_(FK^△ L) =(1/2)FA.KL=(1/2).((b+c)/( (√2))).((b+c)/( (√2)))=(((b+c)^2 )/4) .](https://www.tinkutara.com/question/Q47909.png)
$$#\mathrm{1}. \\ $$$${a}\:{circle}\:{passing}\:{from}:{A},{B},{C},{also} \\ $$$${passes}\:{from}\:{F}.{because}\:{of}: \\ $$$$\measuredangle{BAC}=\measuredangle{BFC}=\mathrm{90}^{\bullet} .{BF}={FC}=\frac{{a}}{\:\sqrt{\mathrm{2}}} \\ $$$${so}\:{B}\overset{{arc}} {{F}}=\overset{{arc}} {{F}C}\Rightarrow{B}\overset{�} {{A}F}={C}\overset{�} {{A}F}.{so} \\ $$$${AF},{is}\:{bisector}\:{of}\:{B}\overset{�} {{A}C}. \\ $$$${or}\:{another}\:{way}: \\ $$$${FA}={x} \\ $$$${cosF}\overset{�} {{A}B}=\frac{{FA}^{\mathrm{2}} +{AB}^{\mathrm{2}} −{FB}^{\mathrm{2}} }{\mathrm{2}{FA}.{AB}}= \\ $$$$=\frac{{x}^{\mathrm{2}} +{c}^{\mathrm{2}} −\left(\frac{{a}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} }{\mathrm{2}{xc}}=\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{c}^{\mathrm{2}} −{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{4}{xc}}= \\ $$$$=\frac{\mathrm{2}{x}^{\mathrm{2}} +{c}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{4}{xc}}\:\:\left({i}\right) \\ $$$${cosF}\overset{�} {{A}C}=\frac{{FA}^{\mathrm{2}} +{AC}^{\mathrm{2}} −{FC}^{\mathrm{2}} }{\mathrm{2}{FA}.{AC}}= \\ $$$$=\frac{{x}^{\mathrm{2}} +{b}^{\mathrm{2}} −\left(\frac{{a}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} }{\mathrm{2}{xb}}=\frac{\mathrm{2}{x}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{4}{xb}}\:\left({ii}\right) \\ $$$$\left({i}\right)−\left({ii}\right)=\frac{{b}\left(\mathrm{2}{x}^{\mathrm{2}} +{c}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)−{c}\left(\mathrm{2}{x}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)}{\mathrm{4}{xbc}}= \\ $$$$=\frac{\mathrm{2}{x}^{\mathrm{2}} \left({b}−{c}\right)−\left({b}^{\mathrm{3}} −{c}^{\mathrm{3}} −{bc}^{\mathrm{2}} +{cb}^{\mathrm{2}} \right)}{\mathrm{4}{xbc}}= \\ $$$$=\frac{\left({b}−{c}\right)\left(\mathrm{2}{x}^{\mathrm{2}} −\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{bc}\right)−{bc}\right)}{\mathrm{4}{xbc}}= \\ $$$$=\frac{\left({b}−{c}\right)\left(\mathrm{2}{x}^{\mathrm{2}} −\left({b}+{c}\right)^{\mathrm{2}} \right)}{\mathrm{4}{xbc}}=\mathrm{0} \\ $$$$\Rightarrow\measuredangle{FAB}=\measuredangle{FAC}\Rightarrow{AF},{is}\:{bisector}. \\ $$$$\left[{ABCF},{is}\:{cyclic}.{so}:\right. \\ $$$$\left.{x}.{a}=\frac{{a}}{\:\sqrt{\mathrm{2}}}.{b}+\frac{{a}}{\:\sqrt{\mathrm{2}}}.{c}\Rightarrow{x}=\frac{{b}+{c}}{\:\sqrt{\mathrm{2}}}\right] \\ $$$$#\mathrm{2}. \\ $$$${the}\:{answer}\:{is}\::{no}. \\ $$$${S}_{{F}\overset{\bigtriangleup} {{K}L}} =\frac{\mathrm{1}}{\mathrm{2}}{FA}.{KL}=\frac{\mathrm{1}}{\mathrm{2}}.\frac{{b}+{c}}{\:\sqrt{\mathrm{2}}}.\frac{{b}+{c}}{\:\sqrt{\mathrm{2}}}=\frac{\left({b}+{c}\right)^{\mathrm{2}} }{\mathrm{4}}\:. \\ $$
Answered by behi83417@gmail.com last updated on 16/Nov/18