Question Number 47915 by behi83417@gmail.com last updated on 16/Nov/18
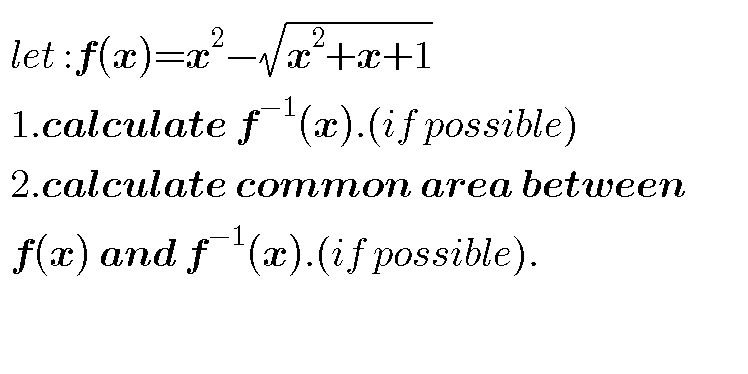
Answered by MJS last updated on 16/Nov/18
![f(x) is kind of a parabola. I don′t think we can find f^(−1) (x) but of course we can approximately calculate the area. area between f and f^(−1) = =2×area between f and y=x x^2 −(√(x^2 +x+1))=x ⇒ x_1 ≈−.557317; x_2 ≈2.27745 2∣∫_x_1 ^x_2 x^2 −x−(√(x^2 +x+1))dx∣= =∣2[(x^3 /3)−(x^2 /2)−(((2x+1)(√(x^2 +x+1)))/4)−((3ln (2x+1+2(√(x^2 +x+1))))/8)]_x_1 ^x_2 ∣≈ ≈6.47706](https://www.tinkutara.com/question/Q47920.png)
$${f}\left({x}\right)\:\mathrm{is}\:\mathrm{kind}\:\mathrm{of}\:\mathrm{a}\:\mathrm{parabola}.\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{we} \\ $$$$\mathrm{can}\:\mathrm{find}\:{f}^{−\mathrm{1}} \left({x}\right)\:\mathrm{but}\:\mathrm{of}\:\mathrm{course}\:\mathrm{we}\:\mathrm{can}\:\mathrm{approximately} \\ $$$$\mathrm{calculate}\:\mathrm{the}\:\mathrm{area}.\:\mathrm{area}\:\mathrm{between}\:{f}\:\mathrm{and}\:{f}^{−\mathrm{1}} = \\ $$$$=\mathrm{2}×\mathrm{area}\:\mathrm{between}\:{f}\:\mathrm{and}\:{y}={x} \\ $$$${x}^{\mathrm{2}} −\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}={x}\:\Rightarrow\:{x}_{\mathrm{1}} \approx−.\mathrm{557317};\:{x}_{\mathrm{2}} \approx\mathrm{2}.\mathrm{27745} \\ $$$$\mathrm{2}\mid\underset{{x}_{\mathrm{1}} } {\overset{{x}_{\mathrm{2}} } {\int}}{x}^{\mathrm{2}} −{x}−\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx}\mid= \\ $$$$=\mid\mathrm{2}\left[\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−\frac{\left(\mathrm{2}{x}+\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{\mathrm{4}}−\frac{\mathrm{3ln}\:\left(\mathrm{2}{x}+\mathrm{1}+\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\right)}{\mathrm{8}}\right]_{{x}_{\mathrm{1}} } ^{{x}_{\mathrm{2}} } \mid\approx \\ $$$$\approx\mathrm{6}.\mathrm{47706} \\ $$
Commented by mr W last updated on 17/Nov/18

$${this}\:{is}\:{only}\:{an}\:{approximation}\:{as}\:{MJS} \\ $$$${sir}\:{said}. \\ $$$${to}\:{be}\:{exact}\:{the}\:{common}\:{area}\:{of}\:{f}\left({x}\right) \\ $$$${and}\:{f}^{−\mathrm{1}} \left({x}\right)\:{is}\:{not}\:{always}\:\mathrm{2}×{area}\:{btw}. \\ $$$${f}\left({x}\right)\:{and}\:{y}={x},\:{as}\:{in}\:{this}\:{case}. \\ $$$${The}\:{common}\:{area}\:{is}\:{the}\:{green}\:{shaded} \\ $$$${area}.\:{But}\:{the}\:{area}\:{between}\:{f}\left({x}\right)\:{and} \\ $$$${y}={x}\:{includes}\:{also}\:{the}\:{blue}\:{shaded}\:{area}. \\ $$
Commented by mr W last updated on 17/Nov/18
Commented by MJS last updated on 17/Nov/18

$$\mathrm{you}'\mathrm{re}\:\mathrm{right} \\ $$$$\mathrm{in}\:\mathrm{our}\:\mathrm{case},\:\mathrm{the}\:\mathrm{common}\:\mathrm{points}\:\notin{y}={x}\:\mathrm{are} \\ $$$$\begin{pmatrix}{\mathrm{0}}\\{−\mathrm{1}}\end{pmatrix}\:\mathrm{and}\:\begin{pmatrix}{−\mathrm{1}}\\{\mathrm{0}}\end{pmatrix}.\:\mathrm{I}'\mathrm{ll}\:\mathrm{try}\:\mathrm{to}\:\mathrm{find}\:\mathrm{this}\:\mathrm{small}\:\mathrm{area}… \\ $$$$ \\ $$$$…\mathrm{because}\:\mathrm{of}\:\mathrm{the}\:\mathrm{symmetry}\:\mathrm{of}\:{f}\:\mathrm{and}\:{f}^{−\mathrm{1}} \:\mathrm{the} \\ $$$$\mathrm{small}\:\mathrm{area}\:\mathrm{is} \\ $$$$\mathrm{2}\left(\mid\underset{−.\mathrm{557317}} {\overset{\mathrm{0}} {\int}}{f}\left({x}\right){dx}\mid−\mid\underset{−\mathrm{1}} {\overset{\mathrm{0}} {\int}}{f}\left({x}\right){dx}−\underset{−.\mathrm{557317}} {\overset{\mathrm{0}} {\int}}\left({f}\left({x}\right)+.\mathrm{557317}\right){dx}\mid\right)=.\mathrm{0133537} \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{resulting}\:\mathrm{area}\:\mathrm{between}\:{f}\:\mathrm{and}\:{f}^{−\mathrm{1}} \:\mathrm{is} \\ $$$$\approx\mathrm{6}.\mathrm{46370} \\ $$
Commented by ajfour last updated on 17/Nov/18
$${I}\:{thought}\:{of}\:{a}\:{way}.. \\ $$
Commented by MJS last updated on 17/Nov/18
$$…\mathrm{still}\:\mathrm{trying}\:\mathrm{to}\:\mathrm{find}\:{f}^{−\mathrm{1}} … \\ $$
Answered by ajfour last updated on 17/Nov/18
![let f^( −1) (x) = y , then x = y^2 −(√(y^2 +y+1)) ⇒ y^2 = x+(√(y^2 +y+1)) let [z(y)]^2 = x−(√(y^2 +y+1)) ⇒ y^2 +z^2 = 2x ...(i) & (y^2 −z^2 )^2 =4(y^2 +y+1 ) ...(ii) So let y = 2xcos θ , z = 2xsin θ Then From (ii) [4x^2 (2cos^2 θ−1)]^2 =4(4x^2 cos^2 θ +2xcos θ+1) ⇒ 4x^4 (4cos^4 θ−4cos^2 θ+1) = 4x^2 cos^2 θ+2xcos θ+1 ⇒ (2xcos θ)^4 −(1+4x^2 )(2xcos θ)^2 −2xcos θ−1 = 0 back again y = 2xcos θ ⇒ y^4 −ay^2 −y−1 = 0 where a = 1+4x^2 Let (y^2 +Ay+B)(y^2 −Ay+C)=0 ⇔ y^4 −ay^2 −y−1 = 0 ⇒ B+C−A^2 = −a A(B−C) = 1 BC = −1 ⇒ (B−C)^2 = (1/A^2 ) ; (B+C)^2 = (A^2 −a)^2 ⇒ (A^2 −a)^2 −(1/A^2 ) = −4 or A^2 (A^2 −a)^2 +4A^2 −1 = 0 let A^2 = s s(s−a)^2 +4s−1 = 0 ........................................ ________________________.](https://www.tinkutara.com/question/Q47974.png)
$${let}\:\:{f}^{\:−\mathrm{1}} \left({x}\right)\:=\:{y}\:,\:{then} \\ $$$$\:\:\:\:{x}\:=\:{y}^{\mathrm{2}} −\sqrt{{y}^{\mathrm{2}} +{y}+\mathrm{1}} \\ $$$$\:\Rightarrow\:\:{y}^{\mathrm{2}} \:=\:{x}+\sqrt{{y}^{\mathrm{2}} +{y}+\mathrm{1}}\: \\ $$$${let}\:\:\left[{z}\left({y}\right)\right]^{\mathrm{2}} \:=\:{x}−\sqrt{{y}^{\mathrm{2}} +{y}+\mathrm{1}}\: \\ $$$$\Rightarrow\:\:\:{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \:=\:\mathrm{2}{x}\:\:\:\:\:…\left({i}\right) \\ $$$$\&\:\:\:\:\left({y}^{\mathrm{2}} −{z}^{\mathrm{2}} \right)^{\mathrm{2}} \:=\mathrm{4}\left({y}^{\mathrm{2}} +{y}+\mathrm{1}\:\right)\:\:…\left({ii}\right) \\ $$$$\:{So}\:{let}\:\:{y}\:=\:\mathrm{2}{x}\mathrm{cos}\:\theta\:,\:{z}\:=\:\mathrm{2}{x}\mathrm{sin}\:\theta \\ $$$$\:\:{Then}\:\:{From}\:\left({ii}\right) \\ $$$$\left[\mathrm{4}{x}^{\mathrm{2}} \left(\mathrm{2cos}\:^{\mathrm{2}} \theta−\mathrm{1}\right)\right]^{\mathrm{2}} =\mathrm{4}\left(\mathrm{4}{x}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{2}{x}\mathrm{cos}\:\theta+\mathrm{1}\right) \\ $$$$\Rightarrow\:\:\mathrm{4}{x}^{\mathrm{4}} \left(\mathrm{4cos}\:^{\mathrm{4}} \theta−\mathrm{4cos}\:^{\mathrm{2}} \theta+\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{4}{x}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta+\mathrm{2}{x}\mathrm{cos}\:\theta+\mathrm{1} \\ $$$$\Rightarrow\:\:\left(\mathrm{2}{x}\mathrm{cos}\:\theta\right)^{\mathrm{4}} −\left(\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} \right)\left(\mathrm{2}{x}\mathrm{cos}\:\theta\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{2}{x}\mathrm{cos}\:\theta−\mathrm{1}\:=\:\mathrm{0} \\ $$$${back}\:{again}\:\:{y}\:=\:\mathrm{2}{x}\mathrm{cos}\:\theta \\ $$$$\Rightarrow\:\:{y}^{\mathrm{4}} −\boldsymbol{{a}}{y}^{\mathrm{2}} −{y}−\mathrm{1}\:=\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{where}\:\:\boldsymbol{{a}}\:=\:\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} \\ $$$${Let}\:\:\:\left({y}^{\mathrm{2}} +{Ay}+{B}\right)\left({y}^{\mathrm{2}} −{Ay}+{C}\right)=\mathrm{0} \\ $$$$\Leftrightarrow\:\:\:{y}^{\mathrm{4}} −{ay}^{\mathrm{2}} −{y}−\mathrm{1}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\:\:\:{B}+{C}−{A}^{\mathrm{2}} \:=\:−{a} \\ $$$$\:\:\:\:\:\:\:\:\:\:{A}\left({B}−{C}\right)\:=\:\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:{BC}\:=\:−\mathrm{1} \\ $$$$\Rightarrow\:\left({B}−{C}\right)^{\mathrm{2}} =\:\frac{\mathrm{1}}{{A}^{\mathrm{2}} }\:\:;\:\left({B}+{C}\right)^{\mathrm{2}} \:=\:\left({A}^{\mathrm{2}} −{a}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\left({A}^{\mathrm{2}} −{a}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{{A}^{\mathrm{2}} }\:=\:−\mathrm{4}\: \\ $$$${or}\:\:\:\:{A}^{\mathrm{2}} \left({A}^{\mathrm{2}} −{a}\right)^{\mathrm{2}} +\mathrm{4}{A}^{\mathrm{2}} −\mathrm{1}\:=\:\mathrm{0} \\ $$$${let}\:\:{A}^{\mathrm{2}} \:=\:{s} \\ $$$$\:\:\:\:\:\:\:{s}\left({s}−{a}\right)^{\mathrm{2}} +\mathrm{4}{s}−\mathrm{1}\:=\:\mathrm{0} \\ $$$$\:\:\:…………………………………. \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_. \\ $$
Commented by ajfour last updated on 17/Nov/18
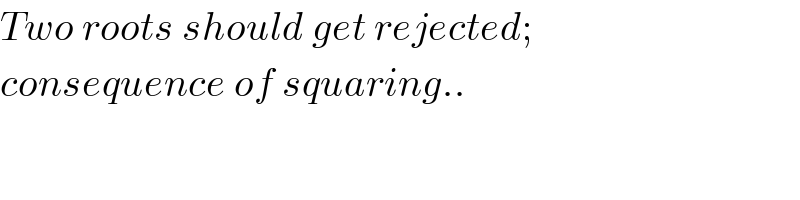
$${Two}\:{roots}\:{should}\:{get}\:{rejected}; \\ $$$${consequence}\:{of}\:{squaring}.. \\ $$
Commented by behi83417@gmail.com last updated on 17/Nov/18
$${thank}\:{you}\:{all}\:{of}\:{my}\:{dears}.{god}\:{bless} \\ $$$${you}\:{all}. \\ $$
