Menu Close

Question-47916

Tinku Tara 0 Comments
Pin




Question Number 47916 by peter frank last updated on 16/Nov/18
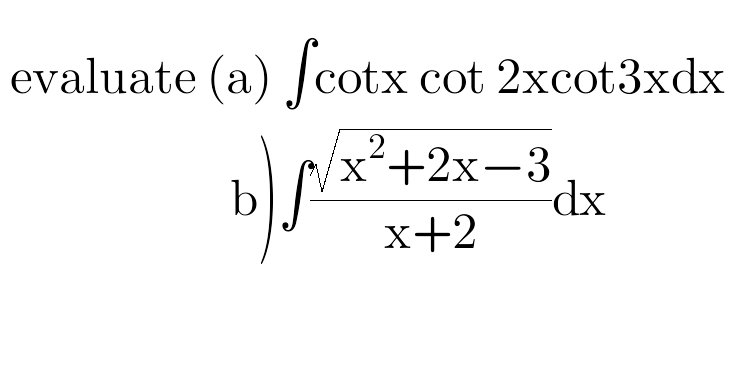
Commented by maxmathsup by imad last updated on 17/Nov/18
b) let I =∫ ((√(x^2 +2x−3))/(x+2)) dx ⇒ I = ∫ ((√((x+1)^2 −4))/(x+2)) dx =_(x+1=2cht) ∫((2(√(ch^2 t−1)))/(2ch(t)−1+2))2sh(t)dt =4 ∫ ((sh^2 t)/(2ch(t) +1)) dt =4 ∫ (((ch(2t)−1)/2)/(2ch(t)+1)) dt=2 ∫ ((ch(2t)−1)/(2ch(t)+1))dt =2 ∫ ((((e^(2t) +e^(−2t) )/(2 ))−1)/(2 ((e^t +e^(−t) )/(2 ))+1))dt = ∫ ((e^(2t) +e^(−2t) −2)/(e^t +e^(−t) +1)) dt =_(e^t =u) ∫ ((u^2 +u^(−2) −2)/(u +u^(−1) +1)) du =∫ ((u^4 +1−2u^2 )/(u^3 +u +u^2 )) du =∫ ((u^4 −2u^2 +1)/(u^3 +u^2 +u)) du =∫ ((u(u^3 +u^2 +u)−u^3 −u^2 −2u^2 +1)/(u^3 +u^2 +u)) du =(u^2 /2) −∫ ((u^3 +3u^2 −1)/(u^3 +u^2 +u)) du = (u^2 /2) −∫ ((u^3 +u^2 +u −u^2 −u +3u^2 −1)/(u^3 +u^2 +u)) du =(u^2 /2) −u −∫ ((2u^2 −u−1)/(u^3 +u^2 +u)) du let decompose F(u) =((2u^2 −u−1)/(u^3 +u^2 +u)) F(u) = (a/u) +((bu +c)/(u^2 +u +1)) a =lim_(u→0) uF(u) =−(1/3) lim_(u→+∞) u F(u)=2 =a +b ⇒b=2+(1/3) =(7/3) ⇒F(u)=−(1/(3u)) +(((7/3)u +c)/(u^2 +u +1)) F(1) =0 =−(1/3) +(1/3)((7/3)+c) ⇒−1+(7/3)+c =0 ⇒c=−(4/3) ⇒ F(u) =−(1/(3u)) +(1/3) ((7u−4)/(u^2 +u +1)) ...be continued...
$$\left.{b}\right)\:{let}\:{I}\:=\int\:\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{3}}}{{x}+\mathrm{2}}\:{dx}\:\Rightarrow\:{I}\:=\:\int\:\frac{\sqrt{\left({x}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}}}{{x}+\mathrm{2}}\:{dx}\:=_{{x}+\mathrm{1}=\mathrm{2}{cht}} \:\int\frac{\mathrm{2}\sqrt{{ch}^{\mathrm{2}} {t}−\mathrm{1}}}{\mathrm{2}{ch}\left({t}\right)−\mathrm{1}+\mathrm{2}}\mathrm{2}{sh}\left({t}\right){dt} \\ $$$$=\mathrm{4}\:\int\:\:\frac{{sh}^{\mathrm{2}} {t}}{\mathrm{2}{ch}\left({t}\right)\:+\mathrm{1}}\:{dt}\:=\mathrm{4}\:\int\:\frac{\frac{{ch}\left(\mathrm{2}{t}\right)−\mathrm{1}}{\mathrm{2}}}{\mathrm{2}{ch}\left({t}\right)+\mathrm{1}}\:{dt}=\mathrm{2}\:\int\:\:\:\frac{{ch}\left(\mathrm{2}{t}\right)−\mathrm{1}}{\mathrm{2}{ch}\left({t}\right)+\mathrm{1}}{dt} \\ $$$$=\mathrm{2}\:\int\:\:\:\frac{\frac{{e}^{\mathrm{2}{t}} +{e}^{−\mathrm{2}{t}} }{\mathrm{2}\:}−\mathrm{1}}{\mathrm{2}\:\frac{{e}^{{t}} \:+{e}^{−{t}} }{\mathrm{2}\:}+\mathrm{1}}{dt}\:=\:\int\:\:\:\frac{{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} −\mathrm{2}}{{e}^{{t}} \:+{e}^{−{t}} \:+\mathrm{1}}\:{dt} \\ $$$$=_{{e}^{{t}} ={u}} \:\:\:\:\:\int\:\:\frac{{u}^{\mathrm{2}} \:+{u}^{−\mathrm{2}} −\mathrm{2}}{{u}\:+{u}^{−\mathrm{1}} \:+\mathrm{1}}\:{du}\:=\int\:\:\:\frac{{u}^{\mathrm{4}} \:+\mathrm{1}−\mathrm{2}{u}^{\mathrm{2}} }{{u}^{\mathrm{3}} \:+{u}\:+{u}^{\mathrm{2}} }\:{du} \\ $$$$=\int\:\:\:\frac{{u}^{\mathrm{4}} −\mathrm{2}{u}^{\mathrm{2}} \:+\mathrm{1}}{{u}^{\mathrm{3}} \:+{u}^{\mathrm{2}} \:+{u}}\:{du}\:=\int\:\:\frac{{u}\left({u}^{\mathrm{3}} \:+{u}^{\mathrm{2}} \:+{u}\right)−{u}^{\mathrm{3}} −{u}^{\mathrm{2}} −\mathrm{2}{u}^{\mathrm{2}} +\mathrm{1}}{{u}^{\mathrm{3}} \:+{u}^{\mathrm{2}} \:+{u}}\:{du} \\ $$$$=\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\:\:−\int\:\frac{{u}^{\mathrm{3}} +\mathrm{3}{u}^{\mathrm{2}} \:−\mathrm{1}}{{u}^{\mathrm{3}} +{u}^{\mathrm{2}} \:+{u}}\:{du}\:=\:\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\:−\int\:\frac{{u}^{\mathrm{3}} \:+{u}^{\mathrm{2}} \:+{u}\:−{u}^{\mathrm{2}} −{u}\:+\mathrm{3}{u}^{\mathrm{2}} −\mathrm{1}}{{u}^{\mathrm{3}} \:+{u}^{\mathrm{2}} \:+{u}}\:{du} \\ $$$$=\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\:−{u}\:−\int\:\:\frac{\mathrm{2}{u}^{\mathrm{2}} −{u}−\mathrm{1}}{{u}^{\mathrm{3}} \:+{u}^{\mathrm{2}} \:+{u}}\:{du}\:{let}\:{decompose}\:{F}\left({u}\right)\:=\frac{\mathrm{2}{u}^{\mathrm{2}} −{u}−\mathrm{1}}{{u}^{\mathrm{3}} +{u}^{\mathrm{2}} \:+{u}} \\ $$$${F}\left({u}\right)\:=\:\frac{{a}}{{u}}\:+\frac{{bu}\:+{c}}{{u}^{\mathrm{2}} \:+{u}\:+\mathrm{1}} \\ $$$${a}\:={lim}_{{u}\rightarrow\mathrm{0}} {uF}\left({u}\right)\:=−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${lim}_{{u}\rightarrow+\infty} {u}\:{F}\left({u}\right)=\mathrm{2}\:={a}\:+{b}\:\Rightarrow{b}=\mathrm{2}+\frac{\mathrm{1}}{\mathrm{3}}\:=\frac{\mathrm{7}}{\mathrm{3}}\:\Rightarrow{F}\left({u}\right)=−\frac{\mathrm{1}}{\mathrm{3}{u}}\:+\frac{\frac{\mathrm{7}}{\mathrm{3}}{u}\:+{c}}{{u}^{\mathrm{2}} \:+{u}\:+\mathrm{1}} \\ $$$${F}\left(\mathrm{1}\right)\:=\mathrm{0}\:=−\frac{\mathrm{1}}{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{7}}{\mathrm{3}}+{c}\right)\:\Rightarrow−\mathrm{1}+\frac{\mathrm{7}}{\mathrm{3}}+{c}\:=\mathrm{0}\:\Rightarrow{c}=−\frac{\mathrm{4}}{\mathrm{3}}\:\Rightarrow \\ $$$${F}\left({u}\right)\:=−\frac{\mathrm{1}}{\mathrm{3}{u}}\:+\frac{\mathrm{1}}{\mathrm{3}}\:\frac{\mathrm{7}{u}−\mathrm{4}}{{u}^{\mathrm{2}} \:+{u}\:+\mathrm{1}}\:\:…{be}\:{continued}… \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 16/Nov/18
b)∫((x^2 +2x−3)/((x+2)(√(x^2 +2x−3)) ))dx ∫(x/( (√(x^2 +2x−3))))−3∫(dx/((x+2)(√(x^2 +2x−3)))) (1/2)∫((2x+2−2)/( (√(x^2 +2x−3))))−3∫(dx/((x+2)(√(x^2 +2x−3)))) (1/2)∫((d(x^2 +2x−3))/( (√(x^2 +2x−3)) ))dx−∫(dx/( (√((x+1)^2 −2^2 ))))−3∫(dx/((x+2)(√(x^2 +2x−3)))) I_1 =(1/2)∫((d(x^2 +2x−3))/( (√(x^2 +2x−3)))) =(1/2)×((√(x^2 +2x−3))/(1/2))=(√(x^2 +2x−3)) +c_1 I_2 =∫(dx/( (√((x+1)^2 −2^2 )) )) =ln{(x+1)+(√((x+1)^2 −2^2 )) =ln{(x+1)+(√(x^2 +2x−3)) }+c_2 I_3 =∫(dx/((x+2)(√(x^2 +2x−3)))) t=(1/(x+2)) x+2=(1/t) dx=((−1)/t^2 )dt ∫((−dt)/(t^2 ×(1/t)×(√(((1/t)−2)^2 +2((1/t)−2)−3)))) ∫((−dt)/(t(√((1/t^2 )−(4/t)+4+(2/t)−4−3)))) ∫((−dt)/(t(√((1−4t+4t^2 +2t−7t^2 )/t^2 )))) ∫((−dt)/( (√(−3t^2 −2t+1)))) ∫((−dt)/( (√(1−3(t^2 +(2/3)t+(1/9)−(1/9)))))) ∫((−dt)/( (√(1−3(t+(1/3))^2 +(1/3))))) ∫((−dt)/( (√((4/3)−3(t+(1/3))^2 )))) ((−1)/( (√3)))∫(dt/( (√(((2/3))^2 −(t+(1/3))^2 )))) ((−1)/( (√3)))×sin^(−1) (((t+(1/3))/(2/3)))+c_3 ((−1)/( (√3)))sin^(−1) ((((1/(x+2))+(1/3))/(2/3)))+c_3 pls add them...
$$\left.{b}\right)\int\frac{{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{3}}{\left({x}+\mathrm{2}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{3}}\:}{dx} \\ $$$$\int\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{3}}}−\mathrm{3}\int\frac{{dx}}{\left({x}+\mathrm{2}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{3}}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{x}+\mathrm{2}−\mathrm{2}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{3}}}−\mathrm{3}\int\frac{{dx}}{\left({x}+\mathrm{2}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{3}}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{3}\right)}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{3}}\:}{dx}−\int\frac{{dx}}{\:\sqrt{\left({x}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} }}−\mathrm{3}\int\frac{{dx}}{\left({x}+\mathrm{2}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{3}}} \\ $$$${I}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{3}\right)}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{3}}}\:=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{3}}}{\frac{\mathrm{1}}{\mathrm{2}}}=\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{3}}\:+{c}_{\mathrm{1}} \\ $$$${I}_{\mathrm{2}} =\int\frac{{dx}}{\:\sqrt{\left({x}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} }\:} \\ $$$$={ln}\left\{\left({x}+\mathrm{1}\right)+\sqrt{\left({x}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} }\:\right. \\ $$$$={ln}\left\{\left({x}+\mathrm{1}\right)+\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{3}}\:\right\}+{c}_{\mathrm{2}} \\ $$$${I}_{\mathrm{3}} =\int\frac{{dx}}{\left({x}+\mathrm{2}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{3}}} \\ $$$${t}=\frac{\mathrm{1}}{{x}+\mathrm{2}}\:\:\:{x}+\mathrm{2}=\frac{\mathrm{1}}{{t}}\:\:\:{dx}=\frac{−\mathrm{1}}{{t}^{\mathrm{2}} }{dt} \\ $$$$\int\frac{−{dt}}{{t}^{\mathrm{2}} ×\frac{\mathrm{1}}{{t}}×\sqrt{\left(\frac{\mathrm{1}}{{t}}−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{2}\left(\frac{\mathrm{1}}{{t}}−\mathrm{2}\right)−\mathrm{3}}} \\ $$$$\int\frac{−{dt}}{{t}\sqrt{\frac{\mathrm{1}}{{t}^{\mathrm{2}} }−\frac{\mathrm{4}}{{t}}+\mathrm{4}+\frac{\mathrm{2}}{{t}}−\mathrm{4}−\mathrm{3}}} \\ $$$$\int\frac{−{dt}}{{t}\sqrt{\frac{\mathrm{1}−\mathrm{4}{t}+\mathrm{4}{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{7}{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} }}} \\ $$$$\int\frac{−{dt}}{\:\sqrt{−\mathrm{3}{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1}}} \\ $$$$\int\frac{−{dt}}{\:\sqrt{\mathrm{1}−\mathrm{3}\left({t}^{\mathrm{2}} +\frac{\mathrm{2}}{\mathrm{3}}{t}+\frac{\mathrm{1}}{\mathrm{9}}−\frac{\mathrm{1}}{\mathrm{9}}\right)}} \\ $$$$\int\frac{−{dt}}{\:\sqrt{\mathrm{1}−\mathrm{3}\left({t}+\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{3}}}} \\ $$$$\int\frac{−{dt}}{\:\sqrt{\frac{\mathrm{4}}{\mathrm{3}}−\mathrm{3}\left({t}+\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} }} \\ $$$$\frac{−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\int\frac{{dt}}{\:\sqrt{\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{2}} −\left({t}+\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} }} \\ $$$$\frac{−\mathrm{1}}{\:\sqrt{\mathrm{3}}}×{sin}^{−\mathrm{1}} \left(\frac{{t}+\frac{\mathrm{1}}{\mathrm{3}}}{\frac{\mathrm{2}}{\mathrm{3}}}\right)+{c}_{\mathrm{3}} \\ $$$$\frac{−\mathrm{1}}{\:\sqrt{\mathrm{3}}}{sin}^{−\mathrm{1}} \left(\frac{\frac{\mathrm{1}}{{x}+\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}}{\frac{\mathrm{2}}{\mathrm{3}}}\right)+{c}_{\mathrm{3}} \\ $$$${pls}\:{add}\:{them}… \\ $$
Commented by peter frank last updated on 16/Nov/18
thank you sir...
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}… \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 17/Nov/18
most welcome...
$${most}\:{welcome}… \\ $$
Commented by malwaan last updated on 17/Nov/18
wonderful
$$\mathrm{wonderful} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 17/Nov/18
∫cotxcot2xcot3xdx =∫((cosxcos2xcos3x)/(sinxsin2xsin3x))dx =∫((cosx(1−2sin^2 x)(4cos^3 x−3cosx))/(sinx×2sinxcosx×(3sinx−4sin^3 x)))dx =∫(((1−2sin^2 x){cosx(4cos^2 x−3)})/(2sin^2 x(3sinx−4sin^3 x)))dx =∫(((1−2sin^2 x)(4−4sin^2 x−3)cosx)/(2sin^2 x(3sinx−4sin^3 x)))dx t=sinx dt=cosxdx ∫(((1−2t^2 )(1−4t^2 ))/(2t^2 (3t−4t^3 )))dt ∫((1−6t^2 +8t^4 )/(2t^3 (3−4t^2 )))dt=(1/2)∫((1−6t^2 +8t^4 )/(t^3 (3−4t^2 ))) ((1−6t^2 +8t^4 )/(t^3 (3−4t^2 )))=(a/t)+(b/t^2 )+(c/t^3 )+((pt+q)/(3−4t^2 )) 1−6t^2 +8t^4 =at^2 (3−4t^2 )+bt(3−4t^2 )+c(3−4t^2 )+(pt+q)t^3 1−6t^2 +8t^4 =t^2 (3a)+t^4 (−4a)+t(3b)+t^3 (−4b)+3c+t^2 (−4c)+t^4 (p)+t^3 (q) 8t^4 −6t^2 +1=t^4 (−4a+p)+t^3 (−4b+q)+t^2 (3a−4c)+t(3b)+3c −4a+p=8 −4b+q=0 3a−4c=−6 3b=0 3c=1 so b=0 q=0 c=(1/3) 3a=−6+4×(1/3)=((−18+4)/3) a=((−14)/9) p=8+4a =8+((4×−14)/9)=((72−56)/9)=((−16)/9) pls wait busy... ∫(a/t)dt+∫(b/t^2 )dt+∫(c/t^3 )dt+∫((pt+q)/(3−4t^2 ))dt =((−14)/9)∫(dt/t)+(1/3)∫(dt/t^3 )+((−16)/9)∫((tdt)/(3−4t^2 )) =((−14)/9)∫(dt/t)+(1/3)∫t^(−3) dt+(2/9)∫((d(3−4t^2 ))/(3−4t^2 )) =((−14)/9)lnt+(1/3)×(1/(−2t^2 ))+(2/9)ln(3−4t^2 ) so ans is =(1/2)[((−14)/9)ln(sinx)−(1/(6sin^2 x))+(2/9)ln(3−4sin^2 x)]+c pls check...
$$ \\ $$$$\int{cotxcot}\mathrm{2}{xcot}\mathrm{3}{xdx} \\ $$$$=\int\frac{{cosxcos}\mathrm{2}{xcos}\mathrm{3}{x}}{{sinxsin}\mathrm{2}{xsin}\mathrm{3}{x}}{dx} \\ $$$$=\int\frac{{cosx}\left(\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} {x}\right)\left(\mathrm{4}{cos}^{\mathrm{3}} {x}−\mathrm{3}{cosx}\right)}{{sinx}×\mathrm{2}{sinxcosx}×\left(\mathrm{3}{sinx}−\mathrm{4}{sin}^{\mathrm{3}} {x}\right)}{dx} \\ $$$$=\int\frac{\left(\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} {x}\right)\left\{{cosx}\left(\mathrm{4}{cos}^{\mathrm{2}} {x}−\mathrm{3}\right)\right\}}{\mathrm{2}{sin}^{\mathrm{2}} {x}\left(\mathrm{3}{sinx}−\mathrm{4}{sin}^{\mathrm{3}} {x}\right)}{dx} \\ $$$$=\int\frac{\left(\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} {x}\right)\left(\mathrm{4}−\mathrm{4}{sin}^{\mathrm{2}} {x}−\mathrm{3}\right){cosx}}{\mathrm{2}{sin}^{\mathrm{2}} {x}\left(\mathrm{3}{sinx}−\mathrm{4}{sin}^{\mathrm{3}} {x}\right)}{dx} \\ $$$${t}={sinx}\:\:\:{dt}={cosxdx} \\ $$$$\int\frac{\left(\mathrm{1}−\mathrm{2}{t}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{4}{t}^{\mathrm{2}} \right)}{\mathrm{2}{t}^{\mathrm{2}} \left(\mathrm{3}{t}−\mathrm{4}{t}^{\mathrm{3}} \right)}{dt} \\ $$$$\int\frac{\mathrm{1}−\mathrm{6}{t}^{\mathrm{2}} +\mathrm{8}{t}^{\mathrm{4}} }{\mathrm{2}{t}^{\mathrm{3}} \left(\mathrm{3}−\mathrm{4}{t}^{\mathrm{2}} \right)}{dt}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}−\mathrm{6}{t}^{\mathrm{2}} +\mathrm{8}{t}^{\mathrm{4}} }{{t}^{\mathrm{3}} \left(\mathrm{3}−\mathrm{4}{t}^{\mathrm{2}} \right)} \\ $$$$\frac{\mathrm{1}−\mathrm{6}{t}^{\mathrm{2}} +\mathrm{8}{t}^{\mathrm{4}} }{{t}^{\mathrm{3}} \left(\mathrm{3}−\mathrm{4}{t}^{\mathrm{2}} \right)}=\frac{{a}}{{t}}+\frac{{b}}{{t}^{\mathrm{2}} }+\frac{{c}}{{t}^{\mathrm{3}} }+\frac{{pt}+{q}}{\mathrm{3}−\mathrm{4}{t}^{\mathrm{2}} } \\ $$$$\mathrm{1}−\mathrm{6}{t}^{\mathrm{2}} +\mathrm{8}{t}^{\mathrm{4}} ={at}^{\mathrm{2}} \left(\mathrm{3}−\mathrm{4}{t}^{\mathrm{2}} \right)+{bt}\left(\mathrm{3}−\mathrm{4}{t}^{\mathrm{2}} \right)+{c}\left(\mathrm{3}−\mathrm{4}{t}^{\mathrm{2}} \right)+\left({pt}+{q}\right){t}^{\mathrm{3}} \\ $$$$\mathrm{1}−\mathrm{6}{t}^{\mathrm{2}} +\mathrm{8}{t}^{\mathrm{4}} ={t}^{\mathrm{2}} \left(\mathrm{3}{a}\right)+{t}^{\mathrm{4}} \left(−\mathrm{4}{a}\right)+{t}\left(\mathrm{3}{b}\right)+{t}^{\mathrm{3}} \left(−\mathrm{4}{b}\right)+\mathrm{3}{c}+{t}^{\mathrm{2}} \left(−\mathrm{4}{c}\right)+{t}^{\mathrm{4}} \left({p}\right)+{t}^{\mathrm{3}} \left({q}\right) \\ $$$$\mathrm{8}{t}^{\mathrm{4}} −\mathrm{6}{t}^{\mathrm{2}} +\mathrm{1}={t}^{\mathrm{4}} \left(−\mathrm{4}{a}+{p}\right)+{t}^{\mathrm{3}} \left(−\mathrm{4}{b}+{q}\right)+{t}^{\mathrm{2}} \left(\mathrm{3}{a}−\mathrm{4}{c}\right)+{t}\left(\mathrm{3}{b}\right)+\mathrm{3}{c} \\ $$$$−\mathrm{4}{a}+{p}=\mathrm{8} \\ $$$$−\mathrm{4}{b}+{q}=\mathrm{0} \\ $$$$\mathrm{3}{a}−\mathrm{4}{c}=−\mathrm{6} \\ $$$$\mathrm{3}{b}=\mathrm{0} \\ $$$$\mathrm{3}{c}=\mathrm{1} \\ $$$${so}\:{b}=\mathrm{0}\:\:\:{q}=\mathrm{0}\:\:{c}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{3}{a}=−\mathrm{6}+\mathrm{4}×\frac{\mathrm{1}}{\mathrm{3}}=\frac{−\mathrm{18}+\mathrm{4}}{\mathrm{3}}\:\:\:{a}=\frac{−\mathrm{14}}{\mathrm{9}} \\ $$$${p}=\mathrm{8}+\mathrm{4}{a} \\ $$$$\:\:=\mathrm{8}+\frac{\mathrm{4}×−\mathrm{14}}{\mathrm{9}}=\frac{\mathrm{72}−\mathrm{56}}{\mathrm{9}}=\frac{−\mathrm{16}}{\mathrm{9}} \\ $$$${pls}\:{wait}\:{busy}… \\ $$$$ \\ $$$$\int\frac{{a}}{{t}}{dt}+\int\frac{{b}}{{t}^{\mathrm{2}} }{dt}+\int\frac{{c}}{{t}^{\mathrm{3}} }{dt}+\int\frac{{pt}+{q}}{\mathrm{3}−\mathrm{4}{t}^{\mathrm{2}} }{dt} \\ $$$$=\frac{−\mathrm{14}}{\mathrm{9}}\int\frac{{dt}}{{t}}+\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dt}}{{t}^{\mathrm{3}} }+\frac{−\mathrm{16}}{\mathrm{9}}\int\frac{{tdt}}{\mathrm{3}−\mathrm{4}{t}^{\mathrm{2}} } \\ $$$$=\frac{−\mathrm{14}}{\mathrm{9}}\int\frac{{dt}}{{t}}+\frac{\mathrm{1}}{\mathrm{3}}\int{t}^{−\mathrm{3}} {dt}+\frac{\mathrm{2}}{\mathrm{9}}\int\frac{{d}\left(\mathrm{3}−\mathrm{4}{t}^{\mathrm{2}} \right)}{\mathrm{3}−\mathrm{4}{t}^{\mathrm{2}} } \\ $$$$=\frac{−\mathrm{14}}{\mathrm{9}}{lnt}+\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{1}}{−\mathrm{2}{t}^{\mathrm{2}} }+\frac{\mathrm{2}}{\mathrm{9}}{ln}\left(\mathrm{3}−\mathrm{4}{t}^{\mathrm{2}} \right) \\ $$$${so}\:{ans}\:{is} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{−\mathrm{14}}{\mathrm{9}}{ln}\left({sinx}\right)−\frac{\mathrm{1}}{\mathrm{6}{sin}^{\mathrm{2}} {x}}+\frac{\mathrm{2}}{\mathrm{9}}{ln}\left(\mathrm{3}−\mathrm{4}{sin}^{\mathrm{2}} {x}\right)\right]+{c} \\ $$$${pls}\:{check}… \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *