Question Number 47960 by Meritguide1234 last updated on 17/Nov/18
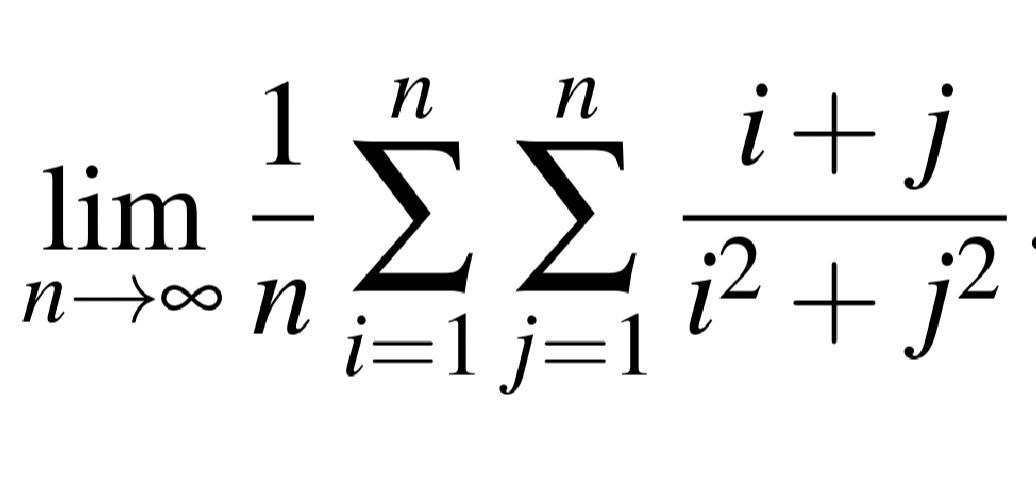
Answered by ajfour last updated on 17/Nov/18
![L=lim_(n→∞) (1/n)Σ_(i=1) ^n Σ_(j=1) ^n ((i+j)/(i^2 +j^2 )) = lim_(n→∞) (1/n)Σ_(i=1) ^n (lim_(n→0) (1/n)Σ_(j=1) ^n (((i/n)+(j/n))/((i^2 /n^2 )+(j^2 /n^2 )))) Let (i/n) = a = lim_(n→∞) (1/n)Σ_(i=1) ^n ∫_0 ^( 1) ((a+x)/(a^2 +x^2 )) dx = lim_(n→∞) (1/n)Σ_(i=1) ^n [∫_0 ^( 1) (a/(a^2 +x^2 )) dx+ (1/2)∫_0 ^( 1) ((2xdx)/(a^2 +x^2 )) ] = lim_(n→∞) (1/n)Σ_(i=1) ^n [tan^(−1) (x/a)∣_0 ^1 +(1/2)ln ∣a^2 +x^2 ∣_0 ^1 ] = lim_(n→∞) (1/n)Σ_(i=1) ^n (tan^(−1) (1/a)+(1/2)ln ∣1+(1/a^2 )∣) = ∫_0 ^( 1) [tan^(−1) (1/x)+(1/2)ln (1+(1/x^2 ))]dx = [xtan^(−1) (1/x)+(1/2)ln (1+(1/x^2 ))]_0 ^1 −∫_0 ^( 1) ((1/(1+(1/x^2 ))))(((−1)/x^2 ))xdx −(1/2)∫_0 ^( 1) ((1/(1+(1/x^2 ))))(((−2)/x^3 ))xdx = (π/4)+((ln 2)/2)+(1/2)∫_0 ^( 1) ((2xdx)/(x^2 +1))+∫_0 ^( 1) (dx/(1+x^2 )) L = (π/4)+((ln 2)/2)+((ln 2)/2)+(π/4) .](https://www.tinkutara.com/question/Q47963.png)
$${L}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\underset{{j}=\mathrm{1}} {\overset{{n}} {\sum}}\:\frac{{i}+{j}}{{i}^{\mathrm{2}} +{j}^{\mathrm{2}} } \\ $$$$\:\:=\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\underset{{n}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{{n}}\underset{{j}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\frac{{i}}{{n}}+\frac{{j}}{{n}}}{\frac{{i}^{\mathrm{2}} }{{n}^{\mathrm{2}} }+\frac{{j}^{\mathrm{2}} }{{n}^{\mathrm{2}} }}\right) \\ $$$${Let}\:\:\frac{{i}}{{n}}\:=\:{a} \\ $$$$\:\:=\:\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\:\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \frac{{a}+{x}}{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} }\:{dx} \\ $$$$\:\:=\:\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\left[\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \frac{{a}}{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} }\:{dx}+\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \frac{\mathrm{2}{xdx}}{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} }\:\:\right] \\ $$$$\:\:=\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\left[\mathrm{tan}^{−\mathrm{1}} \frac{{x}}{{a}}\mid_{\mathrm{0}} ^{\mathrm{1}} \right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid{a}^{\mathrm{2}} +{x}^{\mathrm{2}} \mid_{\mathrm{0}} ^{\mathrm{1}} \:\:\right] \\ $$$$\:\:\:=\:\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\mathrm{1}+\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\mid\right) \\ $$$$\:\:=\:\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \left[\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)\right]{dx} \\ $$$$\:\:=\:\left[{x}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\:\:\:\:\:−\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}\right)\left(\frac{−\mathrm{1}}{{x}^{\mathrm{2}} }\right){xdx} \\ $$$$\:\:\:−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}\right)\left(\frac{−\mathrm{2}}{{x}^{\mathrm{3}} }\right){xdx} \\ $$$$\:=\:\frac{\pi}{\mathrm{4}}+\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \:\frac{\mathrm{2}{xdx}}{{x}^{\mathrm{2}} +\mathrm{1}}+\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$\:{L}\:=\:\frac{\pi}{\mathrm{4}}+\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}+\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\:. \\ $$
Commented by Meritguide1234 last updated on 17/Nov/18
$${beautiful}\:{solution} \\ $$
