Question Number 48027 by ajfour last updated on 18/Nov/18

Commented by ajfour last updated on 18/Nov/18

$${If}\:{OP}\:=\:\mathrm{1}\:{and}\:{all}\:{areas}\:{like} \\ $$$${ABPA}\:\:{are}\:{equal}\:{to}\:{all}\:{areas}\: \\ $$$${like}\:{OBPCO}\:\:{then}\:{find}\:{ellipse} \\ $$$${parameters}\:\boldsymbol{{a}}\:{and}\:\boldsymbol{{b}}. \\ $$
Answered by mr W last updated on 18/Nov/18
![(x^2 /a^2 )+(y^2 /b^2 )=1 r^2 (((cos^2 θ)/a^2 )+((sin^2 θ)/b^2 ))=1 r^2 =((a^2 b^2 )/(a^2 sin^2 θ+b^2 cos^2 θ)) at θ=(π/4): r=1 ⇒a^2 +b^2 =2a^2 b^2 ...(i) ∫_0 ^(π/4) ((r^2 dθ)/2)=(3/4)×((πab)/4) ∫_0 ^(π/4) ((a^2 b^2 dθ)/(a^2 sin^2 θ+b^2 cos^2 θ))=((3πab)/8) [tan^(−1) ((a/b)tan θ)]_0 ^(π/4) =((3π)/8) tan^(−1) ((a/b))=((3π)/8) (a/b)=tan (((3π)/8))=((cos (π/8))/(sin (π/8))) ⇒a=k cos (π/8) ⇒b=k sin (π/8) put this into (i): ⇒k^2 =2k^4 (((sin (π/4))/2))^2 ⇒1=2k^2 ((1/(2(√2))))^2 ⇒k=2 ⇒a=2 cos (π/8) ⇒b=2 sin (π/8)](https://www.tinkutara.com/question/Q48037.png)
$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$${r}^{\mathrm{2}} \left(\frac{\mathrm{cos}^{\mathrm{2}} \:\theta}{{a}^{\mathrm{2}} }+\frac{\mathrm{sin}^{\mathrm{2}} \:\theta}{{b}^{\mathrm{2}} }\right)=\mathrm{1} \\ $$$${r}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta+{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$${at}\:\theta=\frac{\pi}{\mathrm{4}}:\:{r}=\mathrm{1} \\ $$$$\Rightarrow{a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{2}{a}^{\mathrm{2}} {b}^{\mathrm{2}} \:\:\:…\left({i}\right) \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{r}^{\mathrm{2}} {d}\theta}{\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{4}}×\frac{\pi{ab}}{\mathrm{4}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{a}^{\mathrm{2}} {b}^{\mathrm{2}} {d}\theta}{{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta+{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta}=\frac{\mathrm{3}\pi{ab}}{\mathrm{8}} \\ $$$$\left[\mathrm{tan}^{−\mathrm{1}} \left(\frac{{a}}{{b}}\mathrm{tan}\:\theta\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} =\frac{\mathrm{3}\pi}{\mathrm{8}} \\ $$$$\mathrm{tan}^{−\mathrm{1}} \left(\frac{{a}}{{b}}\right)=\frac{\mathrm{3}\pi}{\mathrm{8}} \\ $$$$\frac{{a}}{{b}}=\mathrm{tan}\:\left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)=\frac{\mathrm{cos}\:\frac{\pi}{\mathrm{8}}}{\mathrm{sin}\:\frac{\pi}{\mathrm{8}}} \\ $$$$\Rightarrow{a}={k}\:\mathrm{cos}\:\frac{\pi}{\mathrm{8}} \\ $$$$\Rightarrow{b}={k}\:\mathrm{sin}\:\frac{\pi}{\mathrm{8}} \\ $$$${put}\:{this}\:{into}\:\left({i}\right): \\ $$$$\Rightarrow{k}^{\mathrm{2}} =\mathrm{2}{k}^{\mathrm{4}} \left(\frac{\mathrm{sin}\:\frac{\pi}{\mathrm{4}}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{1}=\mathrm{2}{k}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{k}=\mathrm{2} \\ $$$$\Rightarrow{a}=\mathrm{2}\:\mathrm{cos}\:\frac{\pi}{\mathrm{8}} \\ $$$$\Rightarrow{b}=\mathrm{2}\:\mathrm{sin}\:\frac{\pi}{\mathrm{8}} \\ $$
Commented by ajfour last updated on 18/Nov/18

$${Thank}\:{you}\:\mathcal{SIR}. \\ $$
Answered by ajfour last updated on 18/Nov/18
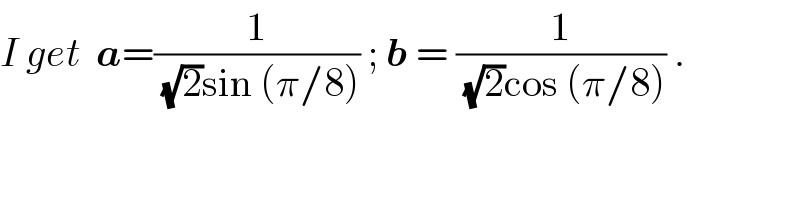
$${I}\:{get}\:\:\boldsymbol{{a}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\mathrm{sin}\:\left(\pi/\mathrm{8}\right)}\:;\:\boldsymbol{{b}}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\mathrm{cos}\:\left(\pi/\mathrm{8}\right)}\:. \\ $$
Commented by mr W last updated on 18/Nov/18
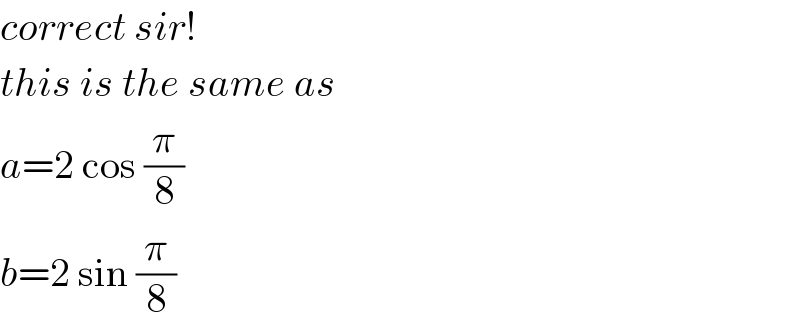
$${correct}\:{sir}! \\ $$$${this}\:{is}\:{the}\:{same}\:{as} \\ $$$${a}=\mathrm{2}\:\mathrm{cos}\:\frac{\pi}{\mathrm{8}} \\ $$$${b}=\mathrm{2}\:\mathrm{sin}\:\frac{\pi}{\mathrm{8}} \\ $$
