Menu Close

Question-48057

Tinku Tara 0 Comments
Pin




Question Number 48057 by F_Nongue last updated on 18/Nov/18
Commented by maxmathsup by imad last updated on 18/Nov/18
I =∫_0 ^1 ((1−x)/(2−x +3−x))dx +∫_1 ^2 ((x−1)/(2−x +3−x)) +∫_2 ^3 ((x−1)/(x−2 +3−x)) +∫_3 ^4 ((x−1)/(x−2 +x−3))dx I =∫_0 ^1 ((1−x)/(−2x+5))dx +∫_1 ^2 ((x−1)/(−2x+5)) dx +∫_2 ^3 (x−1)dx +∫_3 ^4 ((x−1)/(2x−5))dx but ∫_0 ^1 ((1−x)/(−2x+5))dx =∫_0 ^1 ((x−1)/(2x−5))dx =(1/2)∫_0 ^1 ((2x−5 +3)/(2x−5))dx=(1/2) +(3/2) ∫_0 ^1 (dx/(2x−5)) =(1/2) +(3/4)[ln∣2x−5∣]_0 ^1 =(1/2) +(3/4){ln(3)−ln(5)} ∫_1 ^2 ((x−1)/(−2x+5))dx =− ∫_1 ^2 ((x−1)/(2x−5))dx =−(1/2) ∫_1 ^2 ((2x−5 +3)/(2x−5))dx =−(1/2) −(3/2) ∫_1 ^2 (dx/(2x−5)) =−(1/2) −(3/2)[ln∣2x−5∣]_1 ^2 =−(1/2) −(3/2){−ln(3)} ∫_2 ^3 (x−1)dx =[(x^2 /2) −x]_2 ^3 =(9/2) −3 −2+2=(3/2) ∫_3 ^4 ((x−1)/(2x−5))dx =(1/2) +(3/2) ∫_3 ^4 (dx/(2x−5)) =(1/2) +(3/4)[ln∣2x−5∣]_3 ^4 =(1/2) +(3/4){0}=(1/2) ⇒ I =(1/2) +(3/4)ln(3)−(3/4)ln(5)−(1/2) +(3/2)ln(3) +(3/2) +(1/2) I =2 +(9/4)ln(3)−(3/4)ln(5) .
$${I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\mathrm{1}−{x}}{\mathrm{2}−{x}\:+\mathrm{3}−{x}}{dx}\:+\int_{\mathrm{1}} ^{\mathrm{2}} \:\:\frac{{x}−\mathrm{1}}{\mathrm{2}−{x}\:+\mathrm{3}−{x}}\:+\int_{\mathrm{2}} ^{\mathrm{3}} \:\:\frac{{x}−\mathrm{1}}{{x}−\mathrm{2}\:+\mathrm{3}−{x}}\:+\int_{\mathrm{3}} ^{\mathrm{4}} \:\frac{{x}−\mathrm{1}}{{x}−\mathrm{2}\:+{x}−\mathrm{3}}{dx} \\ $$$$\:{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}−{x}}{−\mathrm{2}{x}+\mathrm{5}}{dx}\:+\int_{\mathrm{1}} ^{\mathrm{2}} \:\frac{{x}−\mathrm{1}}{−\mathrm{2}{x}+\mathrm{5}}\:{dx}\:+\int_{\mathrm{2}} ^{\mathrm{3}} \left({x}−\mathrm{1}\right){dx}\:+\int_{\mathrm{3}} ^{\mathrm{4}} \:\frac{{x}−\mathrm{1}}{\mathrm{2}{x}−\mathrm{5}}{dx}\:{but} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}−{x}}{−\mathrm{2}{x}+\mathrm{5}}{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{x}−\mathrm{1}}{\mathrm{2}{x}−\mathrm{5}}{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{x}−\mathrm{5}\:+\mathrm{3}}{\mathrm{2}{x}−\mathrm{5}}{dx}=\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{3}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dx}}{\mathrm{2}{x}−\mathrm{5}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{3}}{\mathrm{4}}\left[{ln}\mid\mathrm{2}{x}−\mathrm{5}\mid\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{3}}{\mathrm{4}}\left\{{ln}\left(\mathrm{3}\right)−{ln}\left(\mathrm{5}\right)\right\} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{2}} \:\frac{{x}−\mathrm{1}}{−\mathrm{2}{x}+\mathrm{5}}{dx}\:=−\:\int_{\mathrm{1}} ^{\mathrm{2}} \:\frac{{x}−\mathrm{1}}{\mathrm{2}{x}−\mathrm{5}}{dx}\:=−\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{1}} ^{\mathrm{2}} \:\frac{\mathrm{2}{x}−\mathrm{5}\:+\mathrm{3}}{\mathrm{2}{x}−\mathrm{5}}{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\:−\frac{\mathrm{3}}{\mathrm{2}}\:\int_{\mathrm{1}} ^{\mathrm{2}} \:\frac{{dx}}{\mathrm{2}{x}−\mathrm{5}}\:=−\frac{\mathrm{1}}{\mathrm{2}}\:−\frac{\mathrm{3}}{\mathrm{2}}\left[{ln}\mid\mathrm{2}{x}−\mathrm{5}\mid\right]_{\mathrm{1}} ^{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{2}}\:−\frac{\mathrm{3}}{\mathrm{2}}\left\{−{ln}\left(\mathrm{3}\right)\right\} \\ $$$$\int_{\mathrm{2}} ^{\mathrm{3}} \left({x}−\mathrm{1}\right){dx}\:=\left[\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:−{x}\right]_{\mathrm{2}} ^{\mathrm{3}} \:=\frac{\mathrm{9}}{\mathrm{2}}\:−\mathrm{3}\:−\mathrm{2}+\mathrm{2}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\int_{\mathrm{3}} ^{\mathrm{4}} \:\frac{{x}−\mathrm{1}}{\mathrm{2}{x}−\mathrm{5}}{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{3}}{\mathrm{2}}\:\int_{\mathrm{3}} ^{\mathrm{4}} \:\frac{{dx}}{\mathrm{2}{x}−\mathrm{5}}\:=\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{3}}{\mathrm{4}}\left[{ln}\mid\mathrm{2}{x}−\mathrm{5}\mid\right]_{\mathrm{3}} ^{\mathrm{4}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{3}}{\mathrm{4}}\left\{\mathrm{0}\right\}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow \\ $$$${I}\:=\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{3}}{\mathrm{4}}{ln}\left(\mathrm{3}\right)−\frac{\mathrm{3}}{\mathrm{4}}{ln}\left(\mathrm{5}\right)−\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{3}}{\mathrm{2}}{ln}\left(\mathrm{3}\right)\:+\frac{\mathrm{3}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${I}\:=\mathrm{2}\:+\frac{\mathrm{9}}{\mathrm{4}}{ln}\left(\mathrm{3}\right)−\frac{\mathrm{3}}{\mathrm{4}}{ln}\left(\mathrm{5}\right)\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 18/Nov/18
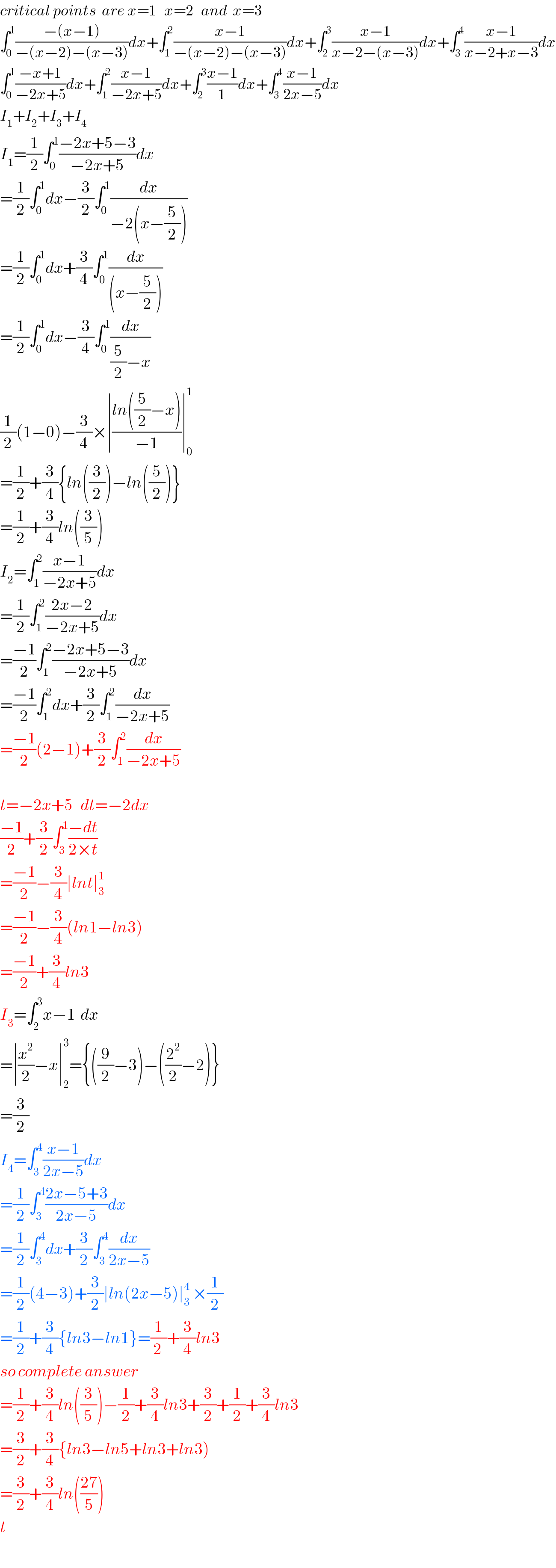
critical points are x=1 x=2 and x=3 ∫_0 ^1 ((−(x−1))/(−(x−2)−(x−3)))dx+∫_1 ^2 ((x−1)/(−(x−2)−(x−3)))dx+∫_2 ^3 ((x−1)/(x−2−(x−3)))dx+∫_3 ^4 ((x−1)/(x−2+x−3))dx ∫_0 ^1 ((−x+1)/(−2x+5))dx+∫_1 ^2 ((x−1)/(−2x+5))dx+∫_2 ^3 ((x−1)/1)dx+∫_3 ^4 ((x−1)/(2x−5))dx I_1 +I_2 +I_3 +I_4 I_1 =(1/2)∫_0 ^1 ((−2x+5−3)/(−2x+5))dx =(1/2)∫_0 ^1 dx−(3/2)∫_0 ^1 (dx/(−2(x−(5/2)))) =(1/2)∫_0 ^1 dx+(3/4)∫_0 ^1 (dx/((x−(5/2)))) =(1/2)∫_0 ^1 dx−(3/4)∫_0 ^1 (dx/((5/2)−x)) (1/2)(1−0)−(3/4)×∣((ln((5/2)−x))/(−1))∣_0 ^1 =(1/2)+(3/4){ln((3/2))−ln((5/2))} =(1/2)+(3/4)ln((3/5)) I_2 =∫_1 ^2 ((x−1)/(−2x+5))dx =(1/2)∫_1 ^2 ((2x−2)/(−2x+5))dx =((−1)/2)∫_1 ^2 ((−2x+5−3)/(−2x+5))dx =((−1)/2)∫_1 ^2 dx+(3/2)∫_1 ^2 (dx/(−2x+5)) =((−1)/2)(2−1)+(3/2)∫_1 ^2 (dx/(−2x+5)) t=−2x+5 dt=−2dx ((−1)/2)+(3/2)∫_3 ^1 ((−dt)/(2×t)) =((−1)/2)−(3/4)∣lnt∣_3 ^1 =((−1)/2)−(3/4)(ln1−ln3) =((−1)/2)+(3/4)ln3 I_3 =∫_2 ^3 x−1 dx =∣(x^2 /2)−x∣_2 ^3 ={((9/2)−3)−((2^2 /2)−2)} =(3/2) I_4 =∫_3 ^4 ((x−1)/(2x−5))dx =(1/2)∫_3 ^4 ((2x−5+3)/(2x−5))dx =(1/2)∫_3 ^4 dx+(3/2)∫_3 ^4 (dx/(2x−5)) =(1/2)(4−3)+(3/2)∣ln(2x−5)∣_3 ^4 ×(1/2) =(1/2)+(3/4){ln3−ln1}=(1/(2 ))+(3/4)ln3 so complete answer =(1/2)+(3/4)ln((3/5))−(1/2)+(3/4)ln3+(3/2)+(1/2)+(3/4)ln3 =(3/2)+(3/4){ln3−ln5+ln3+ln3) =(3/2)+(3/4)ln(((27)/5)) t
$${critical}\:{points}\:\:{are}\:{x}=\mathrm{1}\:\:\:{x}=\mathrm{2}\:\:\:{and}\:\:{x}=\mathrm{3} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{−\left({x}−\mathrm{1}\right)}{−\left({x}−\mathrm{2}\right)−\left({x}−\mathrm{3}\right)}{dx}+\int_{\mathrm{1}} ^{\mathrm{2}} \frac{{x}−\mathrm{1}}{−\left({x}−\mathrm{2}\right)−\left({x}−\mathrm{3}\right)}{dx}+\int_{\mathrm{2}} ^{\mathrm{3}} \frac{{x}−\mathrm{1}}{{x}−\mathrm{2}−\left({x}−\mathrm{3}\right)}{dx}+\int_{\mathrm{3}} ^{\mathrm{4}} \frac{{x}−\mathrm{1}}{{x}−\mathrm{2}+{x}−\mathrm{3}}{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{−{x}+\mathrm{1}}{−\mathrm{2}{x}+\mathrm{5}}{dx}+\int_{\mathrm{1}} ^{\mathrm{2}} \frac{{x}−\mathrm{1}}{−\mathrm{2}{x}+\mathrm{5}}{dx}+\int_{\mathrm{2}} ^{\mathrm{3}} \frac{{x}−\mathrm{1}}{\mathrm{1}}{dx}+\int_{\mathrm{3}} ^{\mathrm{4}} \frac{{x}−\mathrm{1}}{\mathrm{2}{x}−\mathrm{5}}{dx} \\ $$$${I}_{\mathrm{1}} +{I}_{\mathrm{2}} +{I}_{\mathrm{3}} +{I}_{\mathrm{4}} \\ $$$${I}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{−\mathrm{2}{x}+\mathrm{5}−\mathrm{3}}{−\mathrm{2}{x}+\mathrm{5}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} {dx}−\frac{\mathrm{3}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{−\mathrm{2}\left({x}−\frac{\mathrm{5}}{\mathrm{2}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} {dx}+\frac{\mathrm{3}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\left({x}−\frac{\mathrm{5}}{\mathrm{2}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} {dx}−\frac{\mathrm{3}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\frac{\mathrm{5}}{\mathrm{2}}−{x}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{0}\right)−\frac{\mathrm{3}}{\mathrm{4}}×\mid\frac{{ln}\left(\frac{\mathrm{5}}{\mathrm{2}}−{x}\right)}{−\mathrm{1}}\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{4}}\left\{{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)−{ln}\left(\frac{\mathrm{5}}{\mathrm{2}}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{4}}{ln}\left(\frac{\mathrm{3}}{\mathrm{5}}\right) \\ $$$${I}_{\mathrm{2}} =\int_{\mathrm{1}} ^{\mathrm{2}} \frac{{x}−\mathrm{1}}{−\mathrm{2}{x}+\mathrm{5}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\mathrm{2}} \frac{\mathrm{2}{x}−\mathrm{2}}{−\mathrm{2}{x}+\mathrm{5}}{dx} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\mathrm{2}} \frac{−\mathrm{2}{x}+\mathrm{5}−\mathrm{3}}{−\mathrm{2}{x}+\mathrm{5}}{dx} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\mathrm{2}} {dx}+\frac{\mathrm{3}}{\mathrm{2}}\int_{\mathrm{1}} ^{\mathrm{2}} \frac{{dx}}{−\mathrm{2}{x}+\mathrm{5}} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}−\mathrm{1}\right)+\frac{\mathrm{3}}{\mathrm{2}}\int_{\mathrm{1}} ^{\mathrm{2}} \frac{{dx}}{−\mathrm{2}{x}+\mathrm{5}} \\ $$$$ \\ $$$${t}=−\mathrm{2}{x}+\mathrm{5}\:\:\:{dt}=−\mathrm{2}{dx} \\ $$$$\frac{−\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{2}}\int_{\mathrm{3}} ^{\mathrm{1}} \frac{−{dt}}{\mathrm{2}×{t}} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{4}}\mid{lnt}\mid_{\mathrm{3}} ^{\mathrm{1}} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{4}}\left({ln}\mathrm{1}−{ln}\mathrm{3}\right) \\ $$$$=\frac{−\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{4}}{ln}\mathrm{3} \\ $$$${I}_{\mathrm{3}} =\int_{\mathrm{2}} ^{\mathrm{3}} {x}−\mathrm{1}\:\:{dx} \\ $$$$=\mid\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−{x}\mid_{\mathrm{2}} ^{\mathrm{3}} =\left\{\left(\frac{\mathrm{9}}{\mathrm{2}}−\mathrm{3}\right)−\left(\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{2}\right)\right\} \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$${I}_{\mathrm{4}} =\int_{\mathrm{3}} ^{\mathrm{4}} \frac{{x}−\mathrm{1}}{\mathrm{2}{x}−\mathrm{5}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{3}} ^{\mathrm{4}} \frac{\mathrm{2}{x}−\mathrm{5}+\mathrm{3}}{\mathrm{2}{x}−\mathrm{5}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{3}} ^{\mathrm{4}} {dx}+\frac{\mathrm{3}}{\mathrm{2}}\int_{\mathrm{3}} ^{\mathrm{4}} \frac{{dx}}{\mathrm{2}{x}−\mathrm{5}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{4}−\mathrm{3}\right)+\frac{\mathrm{3}}{\mathrm{2}}\mid{ln}\left(\mathrm{2}{x}−\mathrm{5}\right)\mid_{\mathrm{3}} ^{\mathrm{4}} \:×\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{4}}\left\{{ln}\mathrm{3}−{ln}\mathrm{1}\right\}=\frac{\mathrm{1}}{\mathrm{2}\:}+\frac{\mathrm{3}}{\mathrm{4}}{ln}\mathrm{3} \\ $$$${so}\:{complete}\:{answer} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{4}}{ln}\left(\frac{\mathrm{3}}{\mathrm{5}}\right)−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{4}}{ln}\mathrm{3}+\frac{\mathrm{3}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{4}}{ln}\mathrm{3} \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{4}}\left\{{ln}\mathrm{3}−{ln}\mathrm{5}+{ln}\mathrm{3}+{ln}\mathrm{3}\right) \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{4}}{ln}\left(\frac{\mathrm{27}}{\mathrm{5}}\right) \\ $$$${t} \\ $$
Commented by F_Nongue last updated on 18/Nov/18
thanks sir.
Commented by tanmay.chaudhury50@gmail.com last updated on 19/Nov/18
most welvome...
$${most}\:{welvome}… \\ $$
Answered by ajfour last updated on 19/Nov/18
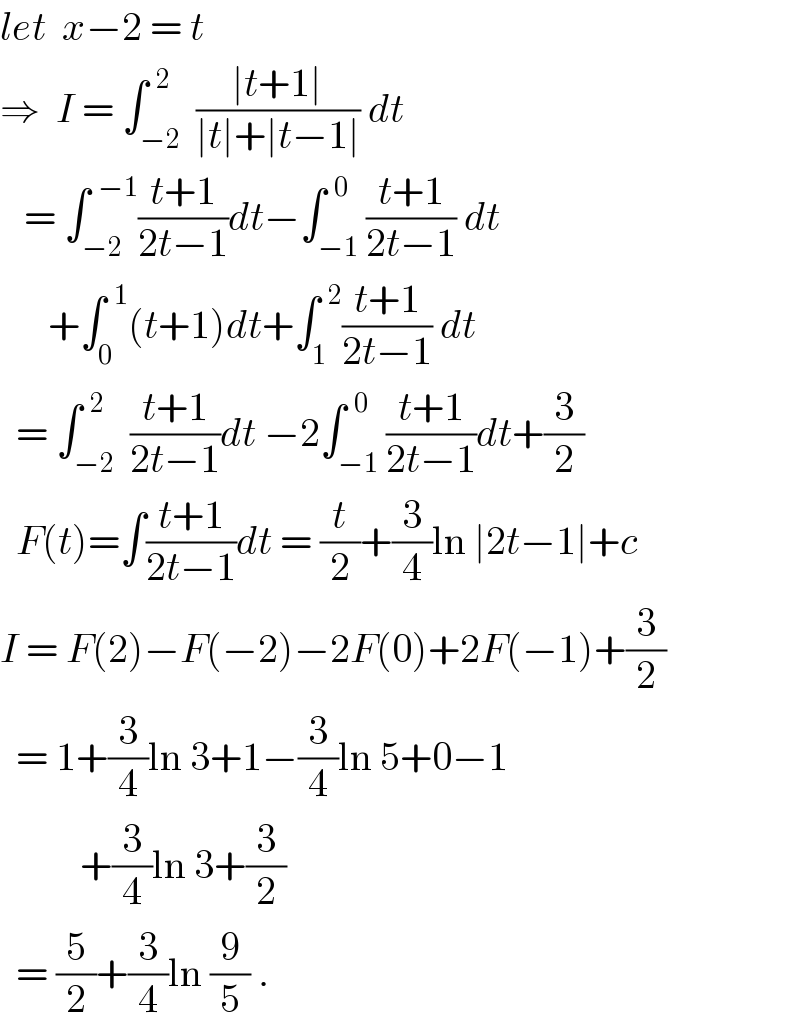
let x−2 = t ⇒ I = ∫_(−2) ^( 2) ((∣t+1∣)/(∣t∣+∣t−1∣)) dt = ∫_(−2) ^( −1) ((t+1)/(2t−1))dt−∫_(−1) ^( 0) ((t+1)/(2t−1)) dt +∫_0 ^( 1) (t+1)dt+∫_1 ^( 2) ((t+1)/(2t−1)) dt = ∫_(−2) ^( 2) ((t+1)/(2t−1))dt −2∫_(−1) ^( 0) ((t+1)/(2t−1))dt+(3/2) F(t)=∫((t+1)/(2t−1))dt = (t/2)+(3/4)ln ∣2t−1∣+c I = F(2)−F(−2)−2F(0)+2F(−1)+(3/2) = 1+(3/4)ln 3+1−(3/4)ln 5+0−1 +(3/4)ln 3+(3/2) = (5/2)+(3/4)ln (9/5) .
$${let}\:\:{x}−\mathrm{2}\:=\:{t} \\ $$$$\Rightarrow\:\:{I}\:=\:\int_{−\mathrm{2}} ^{\:\:\mathrm{2}} \:\frac{\mid{t}+\mathrm{1}\mid}{\mid{t}\mid+\mid{t}−\mathrm{1}\mid}\:{dt} \\ $$$$\:\:\:=\:\int_{−\mathrm{2}} ^{\:\:−\mathrm{1}} \frac{{t}+\mathrm{1}}{\mathrm{2}{t}−\mathrm{1}}{dt}−\int_{−\mathrm{1}} ^{\:\:\mathrm{0}} \frac{{t}+\mathrm{1}}{\mathrm{2}{t}−\mathrm{1}}\:{dt} \\ $$$$\:\:\:\:\:\:+\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \left({t}+\mathrm{1}\right){dt}+\int_{\mathrm{1}} ^{\:\:\mathrm{2}} \frac{{t}+\mathrm{1}}{\mathrm{2}{t}−\mathrm{1}}\:{dt} \\ $$$$\:\:=\:\int_{−\mathrm{2}} ^{\:\:\mathrm{2}} \:\frac{{t}+\mathrm{1}}{\mathrm{2}{t}−\mathrm{1}}{dt}\:−\mathrm{2}\int_{−\mathrm{1}} ^{\:\:\mathrm{0}} \frac{{t}+\mathrm{1}}{\mathrm{2}{t}−\mathrm{1}}{dt}+\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\:\:{F}\left({t}\right)=\int\frac{{t}+\mathrm{1}}{\mathrm{2}{t}−\mathrm{1}}{dt}\:=\:\frac{{t}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{4}}\mathrm{ln}\:\mid\mathrm{2}{t}−\mathrm{1}\mid+{c} \\ $$$${I}\:=\:{F}\left(\mathrm{2}\right)−{F}\left(−\mathrm{2}\right)−\mathrm{2}{F}\left(\mathrm{0}\right)+\mathrm{2}{F}\left(−\mathrm{1}\right)+\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\:\:=\:\mathrm{1}+\frac{\mathrm{3}}{\mathrm{4}}\mathrm{ln}\:\mathrm{3}+\mathrm{1}−\frac{\mathrm{3}}{\mathrm{4}}\mathrm{ln}\:\mathrm{5}+\mathrm{0}−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:+\frac{\mathrm{3}}{\mathrm{4}}\mathrm{ln}\:\mathrm{3}+\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\:\:=\:\frac{\mathrm{5}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{4}}\mathrm{ln}\:\frac{\mathrm{9}}{\mathrm{5}}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *