Question-48113

Question Number 48113 by ajfour last updated on 19/Nov/18

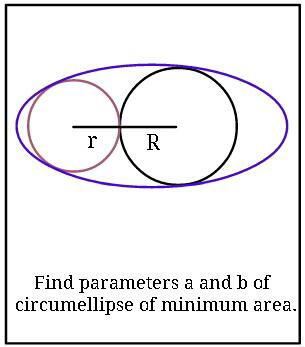
Answered by MJS last updated on 20/Nov/18

circle 1 c_1 : (x+o)^2 +y^2 −o^2 =0 circle 2 c_2 : (x−p)^2 +y^2 −p^2 =0 let 0<o<p ellipse ell: b^2 (x−q)^2 +a^2 y^2 −a^2 b^2 =0 0<o<p ⇒ q>0 c_1 ∩ell={P_1 , P_2 }={ ((x),((−y)) ), ((x),((+y)) )} a^2 c_1 −ell: (a^2 −b^2 )x^2 +2(a^2 o+b^2 q)x+b^2 (a^2 −q^2 )=0 we need B^2 −4AC=0 ⇒ ⇒ a^2 =((b^2 (b^2 +2oq+q^2 ))/(b^2 −o^2 )) same for a^2 c_2 −ell ⇒ ⇒ a^2 =((b^2 (b^2 −2pq+q^2 ))/(b^2 −p^2 )) ((b^2 (b^2 +2oq+q^2 ))/(b^2 −o^2 ))=((b^2 (b^2 −2pq+q^2 ))/(b^2 −p^2 )) ∧ b≠0 ⇒ ⇒ b^2 =((q(2op+q(p−o)))/(2q−(p−o))) ⇒ a^2 =((2q^2 (2op+q(p−o)))/((p−o)(2q−(p−o)))) we now need the minimum of f(q)=ab f(q)=(((2op+q(p−o))(√(2q^3 )))/((2q−(p−o))(√(p−o)))) f′(q)=(√q)×((6q^2 (p−o)+(14op−5(o^2 +p^2 ))q−6op(p−o))/((2q−(p−o))(√(2(p−o))))) f′(q)=0 ∧ q≠0 ⇒ ⇒ q=((5o^2 −14op+5p^2 )/(12(p−o)))±(((o+p)(√(25o^2 −46op+25p^2 )))/(12(p−o))) trying with o=1 and p>1 ⇒ we need the solution with the + so we have a^2 =((2q^2 (2op+q(p−o)))/((p−o)(2q−(p−o)))) b^2 =((q(2op+q(p−o)))/(2q−(p−o))) q=((5o^2 −14op+5p^2 )/(12(p−o)))+(((o+p)(√(25o^2 −46op+25p^2 )))/(12(p−o)))

$$\mathrm{circle}\:\mathrm{1} \\ $$$${c}_{\mathrm{1}} :\:\left({x}+{o}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} −{o}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{circle}\:\mathrm{2} \\ $$$${c}_{\mathrm{2}} :\:\left({x}−{p}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} −{p}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{let}\:\mathrm{0}<{o}<{p} \\ $$$$\mathrm{ellipse} \\ $$$${ell}:\:{b}^{\mathrm{2}} \left({x}−{q}\right)^{\mathrm{2}} +{a}^{\mathrm{2}} {y}^{\mathrm{2}} −{a}^{\mathrm{2}} {b}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{0}<{o}<{p}\:\Rightarrow\:{q}>\mathrm{0} \\ $$$${c}_{\mathrm{1}} \cap{ell}=\left\{{P}_{\mathrm{1}} ,\:{P}_{\mathrm{2}} \right\}=\left\{\begin{pmatrix}{{x}}\\{−{y}}\end{pmatrix},\:\begin{pmatrix}{{x}}\\{+{y}}\end{pmatrix}\right\} \\ $$$${a}^{\mathrm{2}} {c}_{\mathrm{1}} −{ell}: \\ $$$$\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){x}^{\mathrm{2}} +\mathrm{2}\left({a}^{\mathrm{2}} {o}+{b}^{\mathrm{2}} {q}\right){x}+{b}^{\mathrm{2}} \left({a}^{\mathrm{2}} −{q}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{need}\:{B}^{\mathrm{2}} −\mathrm{4}{AC}=\mathrm{0}\:\Rightarrow \\ $$$$\Rightarrow\:{a}^{\mathrm{2}} =\frac{{b}^{\mathrm{2}} \left({b}^{\mathrm{2}} +\mathrm{2}{oq}+{q}^{\mathrm{2}} \right)}{{b}^{\mathrm{2}} −{o}^{\mathrm{2}} } \\ $$$$\mathrm{same}\:\mathrm{for}\:{a}^{\mathrm{2}} {c}_{\mathrm{2}} −{ell}\:\Rightarrow \\ $$$$\Rightarrow\:{a}^{\mathrm{2}} =\frac{{b}^{\mathrm{2}} \left({b}^{\mathrm{2}} −\mathrm{2}{pq}+{q}^{\mathrm{2}} \right)}{{b}^{\mathrm{2}} −{p}^{\mathrm{2}} } \\ $$$$\frac{{b}^{\mathrm{2}} \left({b}^{\mathrm{2}} +\mathrm{2}{oq}+{q}^{\mathrm{2}} \right)}{{b}^{\mathrm{2}} −{o}^{\mathrm{2}} }=\frac{{b}^{\mathrm{2}} \left({b}^{\mathrm{2}} −\mathrm{2}{pq}+{q}^{\mathrm{2}} \right)}{{b}^{\mathrm{2}} −{p}^{\mathrm{2}} }\:\wedge\:{b}\neq\mathrm{0}\:\Rightarrow \\ $$$$\Rightarrow\:{b}^{\mathrm{2}} =\frac{{q}\left(\mathrm{2}{op}+{q}\left({p}−{o}\right)\right)}{\mathrm{2}{q}−\left({p}−{o}\right)} \\ $$$$\Rightarrow\:{a}^{\mathrm{2}} =\frac{\mathrm{2}{q}^{\mathrm{2}} \left(\mathrm{2}{op}+{q}\left({p}−{o}\right)\right)}{\left({p}−{o}\right)\left(\mathrm{2}{q}−\left({p}−{o}\right)\right)} \\ $$$$\mathrm{we}\:\mathrm{now}\:\mathrm{need}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{of}\:{f}\left({q}\right)={ab} \\ $$$${f}\left({q}\right)=\frac{\left(\mathrm{2}{op}+{q}\left({p}−{o}\right)\right)\sqrt{\mathrm{2}{q}^{\mathrm{3}} }}{\left(\mathrm{2}{q}−\left({p}−{o}\right)\right)\sqrt{{p}−{o}}} \\ $$$${f}'\left({q}\right)=\sqrt{{q}}×\frac{\mathrm{6}{q}^{\mathrm{2}} \left({p}−{o}\right)+\left(\mathrm{14}{op}−\mathrm{5}\left({o}^{\mathrm{2}} +{p}^{\mathrm{2}} \right)\right){q}−\mathrm{6}{op}\left({p}−{o}\right)}{\left(\mathrm{2}{q}−\left({p}−{o}\right)\right)\sqrt{\mathrm{2}\left({p}−{o}\right)}} \\ $$$${f}'\left({q}\right)=\mathrm{0}\:\wedge\:{q}\neq\mathrm{0}\:\Rightarrow \\ $$$$\Rightarrow\:{q}=\frac{\mathrm{5}{o}^{\mathrm{2}} −\mathrm{14}{op}+\mathrm{5}{p}^{\mathrm{2}} }{\mathrm{12}\left({p}−{o}\right)}\pm\frac{\left({o}+{p}\right)\sqrt{\mathrm{25}{o}^{\mathrm{2}} −\mathrm{46}{op}+\mathrm{25}{p}^{\mathrm{2}} }}{\mathrm{12}\left({p}−{o}\right)} \\ $$$$\mathrm{trying}\:\mathrm{with}\:{o}=\mathrm{1}\:\mathrm{and}\:{p}>\mathrm{1}\:\Rightarrow\:\mathrm{we}\:\mathrm{need}\:\mathrm{the} \\ $$$$\mathrm{solution}\:\mathrm{with}\:\mathrm{the}\:+ \\ $$$$\mathrm{so}\:\mathrm{we}\:\mathrm{have} \\ $$$${a}^{\mathrm{2}} =\frac{\mathrm{2}{q}^{\mathrm{2}} \left(\mathrm{2}{op}+{q}\left({p}−{o}\right)\right)}{\left({p}−{o}\right)\left(\mathrm{2}{q}−\left({p}−{o}\right)\right)} \\ $$$${b}^{\mathrm{2}} =\frac{{q}\left(\mathrm{2}{op}+{q}\left({p}−{o}\right)\right)}{\mathrm{2}{q}−\left({p}−{o}\right)} \\ $$$${q}=\frac{\mathrm{5}{o}^{\mathrm{2}} −\mathrm{14}{op}+\mathrm{5}{p}^{\mathrm{2}} }{\mathrm{12}\left({p}−{o}\right)}+\frac{\left({o}+{p}\right)\sqrt{\mathrm{25}{o}^{\mathrm{2}} −\mathrm{46}{op}+\mathrm{25}{p}^{\mathrm{2}} }}{\mathrm{12}\left({p}−{o}\right)} \\ $$

Commented by MJS last updated on 20/Nov/18

but there′s a minimum value for q depending on o and p so that the ellipse is touching the 1^(st) circle: q≥((2o(p−o))/(3o−p)). above formula for q meets this at o<p≤((3o)/2). p>((3o)/2) ⇒ smallest ellipse with q=((2o(p−o))/(3o−p)) which indeed makes the smaller circle the osculating circle of the ellipse when p>((3o)/2)

$$\mathrm{but}\:\mathrm{there}'\mathrm{s}\:\mathrm{a}\:\mathrm{minimum}\:\mathrm{value}\:\mathrm{for}\:{q}\:\mathrm{depending} \\ $$$$\mathrm{on}\:{o}\:\mathrm{and}\:{p}\:\mathrm{so}\:\mathrm{that}\:\mathrm{the}\:\mathrm{ellipse}\:\mathrm{is}\:\mathrm{touching}\:\mathrm{the} \\ $$$$\mathrm{1}^{\mathrm{st}} \:\mathrm{circle}:\:{q}\geqslant\frac{\mathrm{2}{o}\left({p}−{o}\right)}{\mathrm{3}{o}−{p}}.\:\mathrm{above}\:\mathrm{formula}\:\mathrm{for}\:{q} \\ $$$$\mathrm{meets}\:\mathrm{this}\:\mathrm{at}\:{o}<{p}\leqslant\frac{\mathrm{3}{o}}{\mathrm{2}}.\:{p}>\frac{\mathrm{3}{o}}{\mathrm{2}}\:\Rightarrow\:\mathrm{smallest} \\ $$$$\mathrm{ellipse}\:\mathrm{with}\:{q}=\frac{\mathrm{2}{o}\left({p}−{o}\right)}{\mathrm{3}{o}−{p}}\:\mathrm{which}\:\mathrm{indeed}\:\mathrm{makes} \\ $$$$\mathrm{the}\:\mathrm{smaller}\:\mathrm{circle}\:\mathrm{the}\:\mathrm{osculating}\:\mathrm{circle}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{ellipse}\:\mathrm{when}\:{p}>\frac{\mathrm{3}{o}}{\mathrm{2}} \\ $$

Commented by ajfour last updated on 20/Nov/18

$${Thank}\:{you}\:{for}\:{as}\:{much},\:{Sir}! \\ $$

Answered by ajfour last updated on 20/Nov/18

Let point of contact of the two circles be the origin O. Eq. of ellipse is_(−) (((x−h)^2 )/a^2 )+(y^2 /b^2 )=1 For general eq. for both circles_(−) (x−ρ)^2 +y^2 = ρ^2 For tangency condition, such a circle and ellipse have one common root. ⇒ eq. below has double root. (((x−h)^2 )/a^2 )+((ρ^2 −(x−ρ)^2 )/b^2 ) = 1 or x^2 ((1/a^2 )−(1/b^2 ))−2x((h/a^2 )−(ρ/b^2 ))+(h^2 /a^2 )−1=0 ⇒ 4((h/a^2 )−(ρ/b^2 ))^2 = 4((1/b^2 )−(1/a^2 ))(1−(h^2 /a^2 )) ⇒ (ρ^2 /b^4 )−((2ρh)/(a^2 b^2 )) = ((1/b^2 )−(1/a^2 ))−(h^2 /(a^2 b^2 )) Above eq. in ρ has two roots ρ = R and ρ = −r ⇒ (R−r)^2 = ((4h^2 b^4 )/a^4 ) & Rr =b^4 [((1/b^2 )−(1/a^2 ))−(h^2 /(a^2 b^2 ))] ⇒ h^2 = ((a^4 (R−r)^2 )/(4b^4 )) and also h^2 = a^2 −b^2 −((a^2 Rr)/b^2 ) ⇒ ((a^4 (R−r)^2 )/(4b^4 )) = a^2 −b^2 −((a^2 Rr)/b^2 ) ⇒ ((a^2 (R−r)^2 )/4) = b^4 −(b^6 /a^2 )−b^2 Rr And area of ellipse = πab let a^2 b^2 = p ⇒ a^2 =(p/b^2 ) further let b^2 = t ⇒ a^2 = (p/t) ((p(R−r)^2 )/(4t)) = t^2 −(t^4 /p)−Rrt ...(I ) For minimum area p is minimum Therefore (dp/dt) = 0 ⇒ −((p(R−r)^2 )/(4t^2 )) = 2t−((4t^3 )/p)−Rr ..(II) (I)+t×(II) yields 0 = 3t^2 −((5t^4 )/p)−2Rrt So p = ((5t^3 )/(3t−2Rr)) ....(i) Now (4/t)×(I)−(II) gives ((5p(R−r)^2 )/(4t^2 )) = 2t−3Rr using (i) in above eq. ((25t(R−r)^2 )/(4(3t−2Rr)))=2t−3Rr ⇒ let z = (t/(Rr)) = (b^2 /(Rr)) , then ((25z(R−r)^2 )/(4Rr(3z−2))) = 2z−3 Also let ((5(R−r))/(2(√(Rr))))= c , then (3z−2)(2z−3) = c^2 z ⇒ 6z^2 −(c^2 +13)z+6 = 0 z = ((c^2 +13±(√((c^2 +13)^2 −144)))/(12)) ⇒ (b^2 /(Rr)) = ((25)/(48))(((R−r)^2 )/(Rr))+((13)/(12)) ±(√((((25)/(48))(((R−r)^2 )/(Rr))+((13)/(12)))^2 −1)) If r = R (b/R) = (√(((13)/(12))±(5/(12)))) but (b/R) > 1 ⇒ + sign gives correct result. b = (√(3/2)) R And generally (b^2 /(Rr)) = ((25(R−r)^2 )/(48Rr))+((13)/(12)) +(√((((25(R−r)^2 )/(48Rr))+((13)/(12)))^2 −1)) using this value in p = ((5t^3 )/(3t−2Rr)) gives a^2 b^2 = ((5b^6 )/(3b^2 −2Rr)) ⇒ (a^2 /(Rr)) = ((5((b^2 /(Rr)))^2 )/(3((b^2 /(Rr)))−2)) As a special case for r = R b = ((√3)/( (√2))) R ; ⇒ (a^2 /R^2 ) =((5((9/4)))/(3((3/2))−2)) = (9/2) ⇒ a = (3/( (√2)))R , b = ((√3)/( (√2)))R _________________________.

$${Let}\:{point}\:{of}\:{contact}\:{of}\:{the}\:{two} \\ $$$${circles}\:{be}\:{the}\:{origin}\:{O}. \\ $$$$\underset{−} {{Eq}.\:{of}\:{ellipse}\:{is}} \\ $$$$\:\:\:\frac{\left({x}−{h}\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\underset{−} {{For}\:{general}\:{eq}.\:{for}\:{both}\:{circles}} \\ $$$$\:\:\:\left({x}−\rho\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\:\rho^{\mathrm{2}} \\ $$$${For}\:{tangency}\:{condition},\:{such}\:{a} \\ $$$${circle}\:{and}\:{ellipse}\:{have}\:{one}\:{common} \\ $$$${root}.\:\Rightarrow\:{eq}.\:{below}\:{has}\:{double}\:{root}. \\ $$$$\:\:\frac{\left({x}−{h}\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{\rho^{\mathrm{2}} −\left({x}−\rho\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }\:=\:\mathrm{1} \\ $$$${or} \\ $$$${x}^{\mathrm{2}} \left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }−\frac{\mathrm{1}}{{b}^{\mathrm{2}} }\right)−\mathrm{2}{x}\left(\frac{{h}}{{a}^{\mathrm{2}} }−\frac{\rho}{{b}^{\mathrm{2}} }\right)+\frac{{h}^{\mathrm{2}} }{{a}^{\mathrm{2}} }−\mathrm{1}=\mathrm{0} \\ $$$$\:\Rightarrow\:\mathrm{4}\left(\frac{{h}}{{a}^{\mathrm{2}} }−\frac{\rho}{{b}^{\mathrm{2}} }\right)^{\mathrm{2}} =\:\mathrm{4}\left(\frac{\mathrm{1}}{{b}^{\mathrm{2}} }−\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{h}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow\:\:\frac{\rho^{\mathrm{2}} }{{b}^{\mathrm{4}} }−\frac{\mathrm{2}\rho{h}}{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }\:=\:\left(\frac{\mathrm{1}}{{b}^{\mathrm{2}} }−\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\right)−\frac{{h}^{\mathrm{2}} }{{a}^{\mathrm{2}} {b}^{\mathrm{2}} } \\ $$$${Above}\:{eq}.\:{in}\:\rho\:{has}\:{two}\:{roots} \\ $$$$\:\:\:\:\rho\:=\:{R}\:\:\:{and}\:\:\rho\:=\:−{r} \\ $$$$\Rightarrow\:\:\left({R}−{r}\right)^{\mathrm{2}} =\:\frac{\mathrm{4}{h}^{\mathrm{2}} {b}^{\mathrm{4}} }{{a}^{\mathrm{4}} }\:\:\:\:\:\& \\ $$$$\:\:\:\:{Rr}\:={b}^{\mathrm{4}} \left[\left(\frac{\mathrm{1}}{{b}^{\mathrm{2}} }−\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\right)−\frac{{h}^{\mathrm{2}} }{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }\right] \\ $$$$\Rightarrow\:\:\:{h}^{\mathrm{2}} \:=\:\frac{{a}^{\mathrm{4}} \left({R}−{r}\right)^{\mathrm{2}} }{\mathrm{4}{b}^{\mathrm{4}} }\:\:\:{and}\:{also} \\ $$$$\:\:\:\:\:\:\:\:{h}^{\mathrm{2}} \:=\:{a}^{\mathrm{2}} −{b}^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} {Rr}}{{b}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:\:\frac{{a}^{\mathrm{4}} \left({R}−{r}\right)^{\mathrm{2}} }{\mathrm{4}{b}^{\mathrm{4}} }\:=\:{a}^{\mathrm{2}} −{b}^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} {Rr}}{{b}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:\:\frac{{a}^{\mathrm{2}} \left({R}−{r}\right)^{\mathrm{2}} }{\mathrm{4}}\:=\:{b}^{\mathrm{4}} −\frac{{b}^{\mathrm{6}} }{{a}^{\mathrm{2}} }−{b}^{\mathrm{2}} {Rr} \\ $$$${And}\:{area}\:{of}\:{ellipse}\:=\:\pi{ab} \\ $$$${let}\:\:\:{a}^{\mathrm{2}} {b}^{\mathrm{2}} \:=\:{p}\:\:\Rightarrow\:\:{a}^{\mathrm{2}} \:=\frac{{p}}{{b}^{\mathrm{2}} } \\ $$$${further}\:{let}\:\:\:{b}^{\mathrm{2}} \:=\:{t}\:\:\Rightarrow\:\:{a}^{\mathrm{2}} \:=\:\frac{{p}}{{t}} \\ $$$$\:\:\:\frac{{p}\left({R}−{r}\right)^{\mathrm{2}} }{\mathrm{4}{t}}\:=\:{t}^{\mathrm{2}} −\frac{{t}^{\mathrm{4}} }{{p}}−{Rrt}\:\:\:…\left({I}\:\right) \\ $$$${For}\:{minimum}\:{area}\:{p}\:{is}\:{minimum} \\ $$$${Therefore}\:\:\:\frac{{dp}}{{dt}}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:−\frac{{p}\left({R}−{r}\right)^{\mathrm{2}} }{\mathrm{4}{t}^{\mathrm{2}} }\:=\:\mathrm{2}{t}−\frac{\mathrm{4}{t}^{\mathrm{3}} }{{p}}−{Rr}\:\:..\left({II}\right) \\ $$$$\left({I}\right)+{t}×\left({II}\right)\:\:{yields} \\ $$$$\:\:\:\mathrm{0}\:=\:\mathrm{3}{t}^{\mathrm{2}} −\frac{\mathrm{5}{t}^{\mathrm{4}} }{{p}}−\mathrm{2}{Rrt} \\ $$$${So}\:\:\:\:\:\boldsymbol{{p}}\:=\:\frac{\mathrm{5}\boldsymbol{{t}}^{\mathrm{3}} }{\mathrm{3}\boldsymbol{{t}}−\mathrm{2}\boldsymbol{{Rr}}}\:\:\:\:\:\:….\left({i}\right) \\ $$$${Now}\:\:\:\frac{\mathrm{4}}{{t}}×\left({I}\right)−\left({II}\right)\:\:{gives} \\ $$$$\:\:\:\frac{\mathrm{5}{p}\left({R}−{r}\right)^{\mathrm{2}} }{\mathrm{4}{t}^{\mathrm{2}} }\:=\:\mathrm{2}{t}−\mathrm{3}{Rr} \\ $$$${using}\:\left({i}\right)\:{in}\:{above}\:{eq}. \\ $$$$\:\:\:\:\:\:\frac{\mathrm{25}{t}\left({R}−{r}\right)^{\mathrm{2}} }{\mathrm{4}\left(\mathrm{3}{t}−\mathrm{2}{Rr}\right)}=\mathrm{2}{t}−\mathrm{3}{Rr} \\ $$$$\Rightarrow\:\:\:{let}\:\:\:{z}\:=\:\frac{{t}}{{Rr}}\:=\:\frac{{b}^{\mathrm{2}} }{{Rr}}\:\:\:,\:{then} \\ $$$$\:\:\:\:\:\frac{\mathrm{25}{z}\left({R}−{r}\right)^{\mathrm{2}} }{\mathrm{4}{Rr}\left(\mathrm{3}{z}−\mathrm{2}\right)}\:=\:\mathrm{2}{z}−\mathrm{3} \\ $$$${Also}\:{let}\:\:\frac{\mathrm{5}\left({R}−{r}\right)}{\mathrm{2}\sqrt{{Rr}}}=\:{c}\:\:,\:{then} \\ $$$$\:\:\:\left(\mathrm{3}{z}−\mathrm{2}\right)\left(\mathrm{2}{z}−\mathrm{3}\right)\:=\:{c}^{\mathrm{2}} {z} \\ $$$$\Rightarrow\:\:\mathrm{6}{z}^{\mathrm{2}} −\left({c}^{\mathrm{2}} +\mathrm{13}\right){z}+\mathrm{6}\:=\:\mathrm{0} \\ $$$$\:\:{z}\:=\:\frac{{c}^{\mathrm{2}} +\mathrm{13}\pm\sqrt{\left({c}^{\mathrm{2}} +\mathrm{13}\right)^{\mathrm{2}} −\mathrm{144}}}{\mathrm{12}} \\ $$$$\Rightarrow\:\frac{{b}^{\mathrm{2}} }{{Rr}}\:=\:\frac{\mathrm{25}}{\mathrm{48}}\frac{\left({R}−{r}\right)^{\mathrm{2}} }{{Rr}}+\frac{\mathrm{13}}{\mathrm{12}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\pm\sqrt{\left(\frac{\mathrm{25}}{\mathrm{48}}\frac{\left({R}−{r}\right)^{\mathrm{2}} }{{Rr}}+\frac{\mathrm{13}}{\mathrm{12}}\right)^{\mathrm{2}} −\mathrm{1}} \\ $$$${If}\:\:\:{r}\:=\:{R} \\ $$$$\:\:\:\:\:\:\:\frac{{b}}{{R}}\:=\:\sqrt{\frac{\mathrm{13}}{\mathrm{12}}\pm\frac{\mathrm{5}}{\mathrm{12}}} \\ $$$$\:\:{but}\:\:\:\frac{{b}}{{R}}\:>\:\mathrm{1}\:\:\:\Rightarrow\:\:+\:{sign}\:{gives} \\ $$$${correct}\:{result}.\:\:\:{b}\:=\:\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\:{R}\: \\ $$$${And}\:{generally} \\ $$$$\:\:\frac{\boldsymbol{{b}}^{\mathrm{2}} }{\boldsymbol{{Rr}}}\:=\:\frac{\mathrm{25}\left(\boldsymbol{{R}}−\boldsymbol{{r}}\right)^{\mathrm{2}} }{\mathrm{48}\boldsymbol{{Rr}}}+\frac{\mathrm{13}}{\mathrm{12}} \\ $$$$\:\:\:\:\:\:\:\:+\sqrt{\left(\frac{\mathrm{25}\left(\boldsymbol{{R}}−\boldsymbol{{r}}\right)^{\mathrm{2}} }{\mathrm{48}\boldsymbol{{Rr}}}+\frac{\mathrm{13}}{\mathrm{12}}\right)^{\mathrm{2}} −\mathrm{1}}\: \\ $$$${using}\:{this}\:{value}\:{in}\:\: \\ $$$$\:\:\:\:\:\:\boldsymbol{{p}}\:=\:\frac{\mathrm{5}\boldsymbol{{t}}^{\mathrm{3}} }{\mathrm{3}\boldsymbol{{t}}−\mathrm{2}\boldsymbol{{Rr}}}\:\:\:{gives} \\ $$$$\:\:\:\:{a}^{\mathrm{2}} {b}^{\mathrm{2}} \:=\:\frac{\mathrm{5}{b}^{\mathrm{6}} }{\mathrm{3}{b}^{\mathrm{2}} −\mathrm{2}{Rr}} \\ $$$$\:\Rightarrow\:\:\:\:\frac{\boldsymbol{{a}}^{\mathrm{2}} }{\boldsymbol{{Rr}}}\:=\:\frac{\mathrm{5}\left(\frac{\boldsymbol{{b}}^{\mathrm{2}} }{\boldsymbol{{Rr}}}\right)^{\mathrm{2}} }{\mathrm{3}\left(\frac{\boldsymbol{{b}}^{\mathrm{2}} }{\boldsymbol{{Rr}}}\right)−\mathrm{2}}\: \\ $$$$\:{As}\:{a}\:{special}\:{case}\:\:{for}\:\:{r}\:=\:{R}\: \\ $$$$\:\:\:\:\:\:\:{b}\:=\:\frac{\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{2}}}\:{R}\:\:\:;\:\: \\ $$$$\Rightarrow\:\:\:\frac{{a}^{\mathrm{2}} }{{R}^{\mathrm{2}} }\:=\frac{\mathrm{5}\left(\frac{\mathrm{9}}{\mathrm{4}}\right)}{\mathrm{3}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)−\mathrm{2}}\:=\:\frac{\mathrm{9}}{\mathrm{2}} \\ $$$$\:\:\Rightarrow\:\:\:{a}\:=\:\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}{R}\:,\:\:{b}\:=\:\frac{\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{2}}}{R}\: \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_. \\ $$

Commented by MJS last updated on 20/Nov/18

my solution includes the same issue. before trying to find the minimum of ab we have q as parameter. obviously there are borders for q depending on the values of o and p (r and R)

$$\mathrm{my}\:\mathrm{solution}\:\mathrm{includes}\:\mathrm{the}\:\mathrm{same}\:\mathrm{issue}. \\ $$$$\mathrm{before}\:\mathrm{trying}\:\mathrm{to}\:\mathrm{find}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{of}\:{ab}\:\mathrm{we} \\ $$$$\mathrm{have}\:{q}\:\mathrm{as}\:\mathrm{parameter}.\:\mathrm{obviously}\:\mathrm{there}\:\mathrm{are} \\ $$$$\mathrm{borders}\:\mathrm{for}\:{q}\:\mathrm{depending}\:\mathrm{on}\:\mathrm{the}\:\mathrm{values}\:\mathrm{of} \\ $$$${o}\:\mathrm{and}\:{p}\:\left({r}\:\mathrm{and}\:{R}\right) \\ $$

Commented by mr W last updated on 20/Nov/18

very nice method sir! but it seems to work only for cases where R and r are not very different. For r<R/2 the results seem not to be correct. I am showing two cases: r=6, R=8 and r=3, R=8

$${very}\:{nice}\:{method}\:{sir}! \\ $$$${but}\:{it}\:{seems}\:{to}\:{work}\:{only}\:{for}\:{cases} \\ $$$${where}\:{R}\:{and}\:{r}\:{are}\:{not}\:{very}\:{different}. \\ $$$${For}\:{r}<{R}/\mathrm{2}\:{the}\:{results}\:{seem}\:{not}\:{to}\:{be} \\ $$$${correct}. \\ $$$${I}\:{am}\:{showing}\:{two}\:{cases}: \\ $$$${r}=\mathrm{6},\:{R}=\mathrm{8}\:{and}\:{r}=\mathrm{3},\:{R}=\mathrm{8} \\ $$

Commented by mr W last updated on 20/Nov/18