Question-48127

Question Number 48127 by cesar.marval.larez@gmail.com last updated on 19/Nov/18

Answered by tanmay.chaudhury50@gmail.com last updated on 19/Nov/18

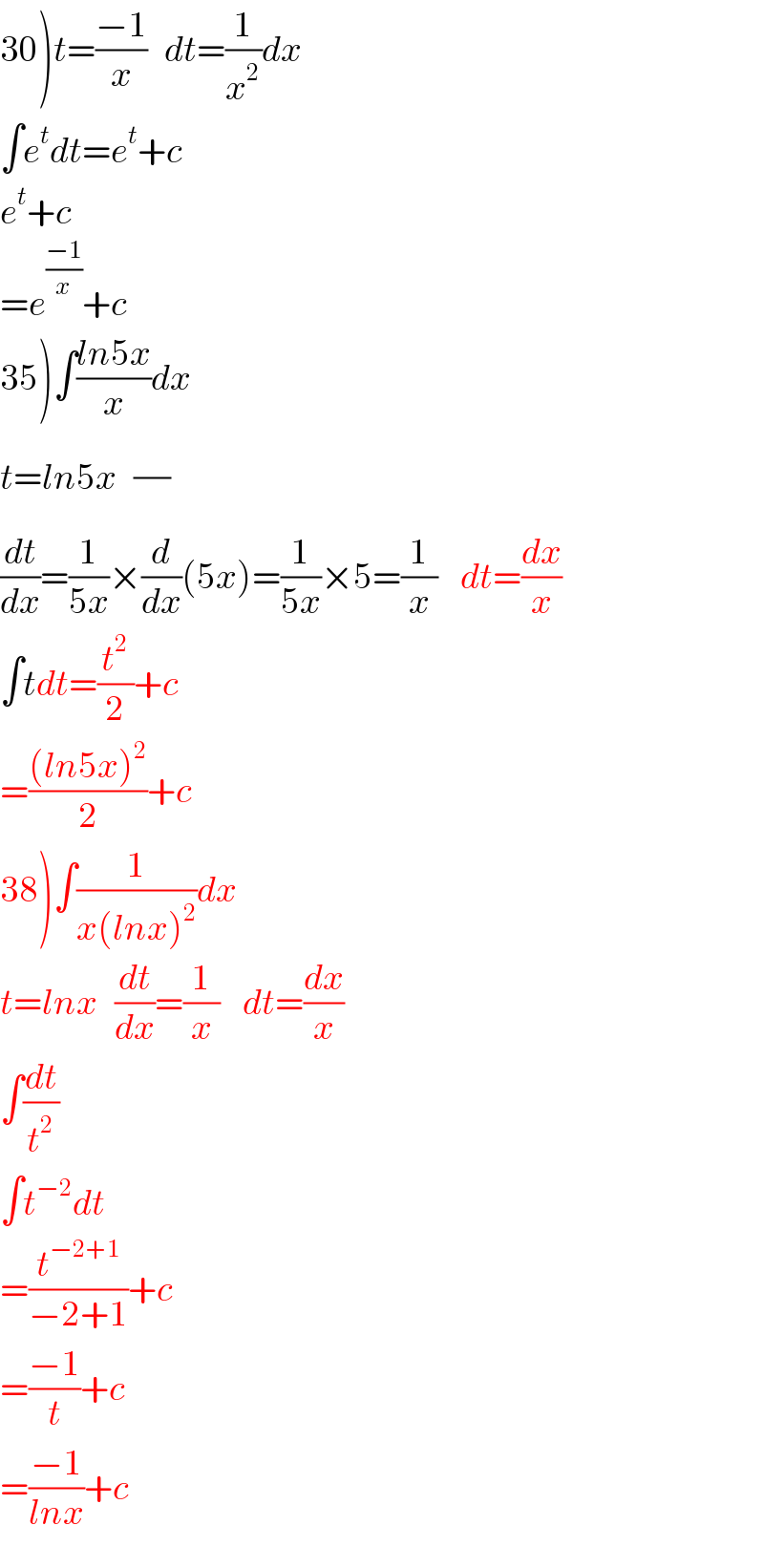
30)t=((−1)/x) dt=(1/x^2 )dx ∫e^t dt=e^t +c e^t +c =e^((−1)/x) +c 35)∫((ln5x)/x)dx t=ln5x (/) (dt/dx)=(1/(5x))×(d/dx)(5x)=(1/(5x))×5=(1/x) dt=(dx/x) ∫tdt=(t^2 /2)+c =(((ln5x)^2 )/2)+c 38)∫(1/(x(lnx)^2 ))dx t=lnx (dt/dx)=(1/x) dt=(dx/x) ∫(dt/t^2 ) ∫t^(−2) dt =(t^(−2+1) /(−2+1))+c =((−1)/t)+c =((−1)/(lnx))+c

$$\left.\mathrm{30}\right){t}=\frac{−\mathrm{1}}{{x}}\:\:\:{dt}=\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{dx} \\ $$$$\int{e}^{{t}} {dt}={e}^{{t}} +{c} \\ $$$${e}^{{t}} +{c} \\ $$$$={e}^{\frac{−\mathrm{1}}{{x}}} +{c} \\ $$$$\left.\mathrm{35}\right)\int\frac{{ln}\mathrm{5}{x}}{{x}}{dx} \\ $$$${t}={ln}\mathrm{5}{x}\:\:\:\frac{}{} \\ $$$$\frac{{dt}}{{dx}}=\frac{\mathrm{1}}{\mathrm{5}{x}}×\frac{{d}}{{dx}}\left(\mathrm{5}{x}\right)=\frac{\mathrm{1}}{\mathrm{5}{x}}×\mathrm{5}=\frac{\mathrm{1}}{{x}}\:\:\:\:{dt}=\frac{{dx}}{{x}} \\ $$$$\int{tdt}=\frac{{t}^{\mathrm{2}} }{\mathrm{2}}+{c}\:\:\: \\ $$$$=\frac{\left({ln}\mathrm{5}{x}\right)^{\mathrm{2}} }{\mathrm{2}}+{c} \\ $$$$\left.\mathrm{38}\right)\int\frac{\mathrm{1}}{{x}\left({lnx}\right)^{\mathrm{2}} }{dx} \\ $$$${t}={lnx}\:\:\:\frac{{dt}}{{dx}}=\frac{\mathrm{1}}{{x}}\:\:\:\:{dt}=\frac{{dx}}{{x}} \\ $$$$\int\frac{{dt}}{{t}^{\mathrm{2}} } \\ $$$$\int{t}^{−\mathrm{2}} {dt} \\ $$$$=\frac{{t}^{−\mathrm{2}+\mathrm{1}} }{−\mathrm{2}+\mathrm{1}}+{c} \\ $$$$=\frac{−\mathrm{1}}{{t}}+{c} \\ $$$$=\frac{−\mathrm{1}}{{lnx}}+{c} \\ $$

Commented by cesar.marval.larez@gmail.com last updated on 19/Nov/18

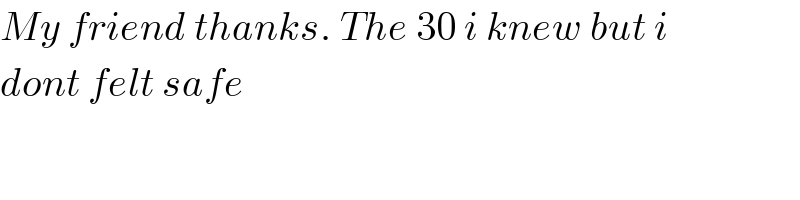
My friend thanks. The 30 i knew but i dont felt safe

$${My}\:{friend}\:{thanks}.\:{The}\:\mathrm{30}\:{i}\:{knew}\:{but}\:{i} \\ $$$${dont}\:{felt}\:{safe} \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 19/Nov/18

$${most}\:{welcome}… \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply