Menu Close

Question-48156

Tinku Tara 0 Comments
Pin




Question Number 48156 by ajfour last updated on 20/Nov/18
Commented by ajfour last updated on 20/Nov/18
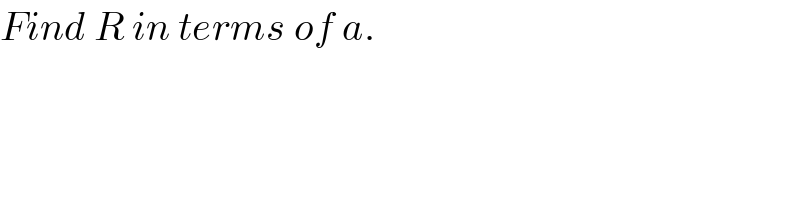
Find R in terms of a.
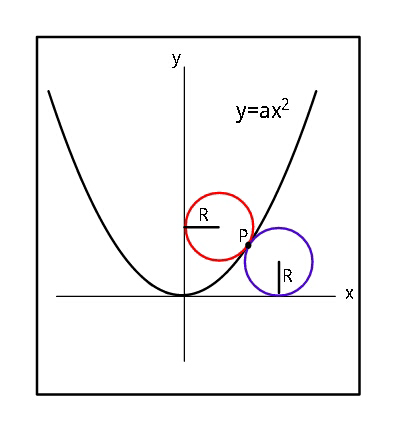
$${Find}\:{R}\:{in}\:{terms}\:{of}\:{a}. \\ $$
Answered by ajfour last updated on 20/Nov/18
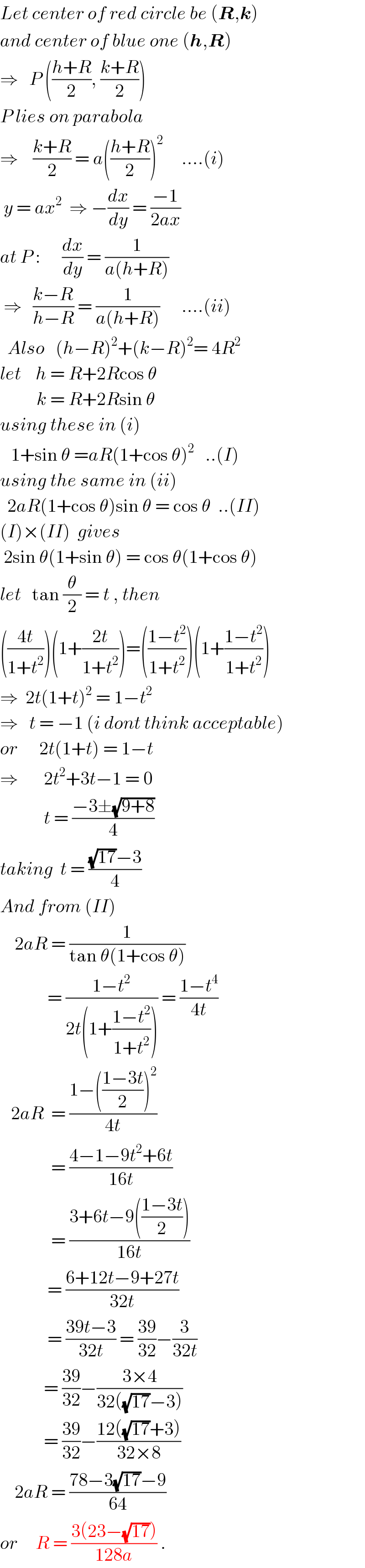
Let center of red circle be (R,k) and center of blue one (h,R) ⇒ P (((h+R)/2), ((k+R)/2)) P lies on parabola ⇒ ((k+R)/2) = a(((h+R)/2))^2 ....(i) y = ax^2 ⇒ −(dx/dy) = ((−1)/(2ax)) at P : (dx/dy) = (1/(a(h+R))) ⇒ ((k−R)/(h−R)) = (1/(a(h+R))) ....(ii) Also (h−R)^2 +(k−R)^2 = 4R^2 let h = R+2Rcos θ k = R+2Rsin θ using these in (i) 1+sin θ =aR(1+cos θ)^2 ..(I) using the same in (ii) 2aR(1+cos θ)sin θ = cos θ ..(II) (I)×(II) gives 2sin θ(1+sin θ) = cos θ(1+cos θ) let tan (θ/2) = t , then (((4t)/(1+t^2 )))(1+((2t)/(1+t^2 )))=(((1−t^2 )/(1+t^2 )))(1+((1−t^2 )/(1+t^2 ))) ⇒ 2t(1+t)^2 = 1−t^2 ⇒ t = −1 (i dont think acceptable) or 2t(1+t) = 1−t ⇒ 2t^2 +3t−1 = 0 t = ((−3±(√(9+8)))/4) taking t = (((√(17))−3)/4) And from (II) 2aR = (1/(tan θ(1+cos θ))) = ((1−t^2 )/(2t(1+((1−t^2 )/(1+t^2 ))))) = ((1−t^4 )/(4t)) 2aR = ((1−(((1−3t)/2))^2 )/(4t)) = ((4−1−9t^2 +6t)/(16t)) = ((3+6t−9(((1−3t)/2)))/(16t)) = ((6+12t−9+27t)/(32t)) = ((39t−3)/(32t)) = ((39)/(32))−(3/(32t)) = ((39)/(32))−((3×4)/(32((√(17))−3))) = ((39)/(32))−((12((√(17))+3))/(32×8)) 2aR = ((78−3(√(17))−9)/(64)) or R = ((3(23−(√(17))))/(128a)) .
$${Let}\:{center}\:{of}\:{red}\:{circle}\:{be}\:\left(\boldsymbol{{R}},\boldsymbol{{k}}\right) \\ $$$${and}\:{center}\:{of}\:{blue}\:{one}\:\left(\boldsymbol{{h}},\boldsymbol{{R}}\right) \\ $$$$\Rightarrow\:\:\:{P}\:\left(\frac{{h}+{R}}{\mathrm{2}},\:\frac{{k}+{R}}{\mathrm{2}}\right) \\ $$$${P}\:{lies}\:{on}\:{parabola} \\ $$$$\Rightarrow\:\:\:\:\frac{{k}+{R}}{\mathrm{2}}\:=\:{a}\left(\frac{{h}+{R}}{\mathrm{2}}\right)^{\mathrm{2}} \:\:\:\:\:….\left({i}\right) \\ $$$$\:{y}\:=\:{ax}^{\mathrm{2}} \:\:\Rightarrow\:−\frac{{dx}}{{dy}}\:=\:\frac{−\mathrm{1}}{\mathrm{2}{ax}}\: \\ $$$${at}\:{P}\::\:\:\:\:\:\:\frac{{dx}}{{dy}}\:=\:\frac{\mathrm{1}}{{a}\left({h}+{R}\right)} \\ $$$$\:\Rightarrow\:\:\:\frac{{k}−{R}}{{h}−{R}}\:=\:\frac{\mathrm{1}}{{a}\left({h}+{R}\right)}\:\:\:\:\:\:….\left({ii}\right) \\ $$$$\:\:{Also}\:\:\:\left({h}−{R}\right)^{\mathrm{2}} +\left({k}−{R}\right)^{\mathrm{2}} =\:\mathrm{4}{R}^{\mathrm{2}} \\ $$$${let}\:\:\:\:{h}\:=\:{R}+\mathrm{2}{R}\mathrm{cos}\:\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:{k}\:=\:{R}+\mathrm{2}{R}\mathrm{sin}\:\theta \\ $$$${using}\:{these}\:{in}\:\left({i}\right) \\ $$$$\:\:\:\mathrm{1}+\mathrm{sin}\:\theta\:={aR}\left(\mathrm{1}+\mathrm{cos}\:\theta\right)^{\mathrm{2}} \:\:\:..\left({I}\right) \\ $$$${using}\:{the}\:{same}\:{in}\:\left({ii}\right) \\ $$$$\:\:\mathrm{2}{aR}\left(\mathrm{1}+\mathrm{cos}\:\theta\right)\mathrm{sin}\:\theta\:=\:\mathrm{cos}\:\theta\:\:..\left({II}\right) \\ $$$$\left({I}\right)×\left({II}\right)\:\:{gives} \\ $$$$\:\mathrm{2sin}\:\theta\left(\mathrm{1}+\mathrm{sin}\:\theta\right)\:=\:\mathrm{cos}\:\theta\left(\mathrm{1}+\mathrm{cos}\:\theta\right) \\ $$$${let}\:\:\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}\:=\:{t}\:,\:{then} \\ $$$$\left(\frac{\mathrm{4}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\right)\left(\mathrm{1}+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\right)=\left(\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)\left(\mathrm{1}+\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow\:\:\mathrm{2}{t}\left(\mathrm{1}+{t}\right)^{\mathrm{2}} \:=\:\mathrm{1}−{t}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:{t}\:=\:−\mathrm{1}\:\left({i}\:{dont}\:{think}\:{acceptable}\right) \\ $$$${or}\:\:\:\:\:\:\mathrm{2}{t}\left(\mathrm{1}+{t}\right)\:=\:\mathrm{1}−{t} \\ $$$$\Rightarrow\:\:\:\:\:\:\:\mathrm{2}{t}^{\mathrm{2}} +\mathrm{3}{t}−\mathrm{1}\:=\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{t}\:=\:\frac{−\mathrm{3}\pm\sqrt{\mathrm{9}+\mathrm{8}}}{\mathrm{4}}\: \\ $$$${taking}\:\:{t}\:=\:\frac{\sqrt{\mathrm{17}}−\mathrm{3}}{\mathrm{4}} \\ $$$${And}\:{from}\:\left({II}\right) \\ $$$$\:\:\:\:\mathrm{2}{aR}\:=\:\frac{\mathrm{1}}{\mathrm{tan}\:\theta\left(\mathrm{1}+\mathrm{cos}\:\theta\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{2}{t}\left(\mathrm{1}+\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)}\:=\:\frac{\mathrm{1}−{t}^{\mathrm{4}} }{\mathrm{4}{t}} \\ $$$$\:\:\:\mathrm{2}{aR}\:\:=\:\frac{\mathrm{1}−\left(\frac{\mathrm{1}−\mathrm{3}{t}}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{4}{t}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{4}−\mathrm{1}−\mathrm{9}{t}^{\mathrm{2}} +\mathrm{6}{t}}{\mathrm{16}{t}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{3}+\mathrm{6}{t}−\mathrm{9}\left(\frac{\mathrm{1}−\mathrm{3}{t}}{\mathrm{2}}\right)}{\mathrm{16}{t}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{6}+\mathrm{12}{t}−\mathrm{9}+\mathrm{27}{t}}{\mathrm{32}{t}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{39}{t}−\mathrm{3}}{\mathrm{32}{t}}\:=\:\frac{\mathrm{39}}{\mathrm{32}}−\frac{\mathrm{3}}{\mathrm{32}{t}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{39}}{\mathrm{32}}−\frac{\mathrm{3}×\mathrm{4}}{\mathrm{32}\left(\sqrt{\mathrm{17}}−\mathrm{3}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{39}}{\mathrm{32}}−\frac{\mathrm{12}\left(\sqrt{\mathrm{17}}+\mathrm{3}\right)}{\mathrm{32}×\mathrm{8}} \\ $$$$\:\:\:\:\mathrm{2}{aR}\:=\:\frac{\mathrm{78}−\mathrm{3}\sqrt{\mathrm{17}}−\mathrm{9}}{\mathrm{64}} \\ $$$${or}\:\:\:\:\:{R}\:=\:\frac{\mathrm{3}\left(\mathrm{23}−\sqrt{\mathrm{17}}\right)}{\mathrm{128}{a}}\:. \\ $$
Commented by ajfour last updated on 20/Nov/18
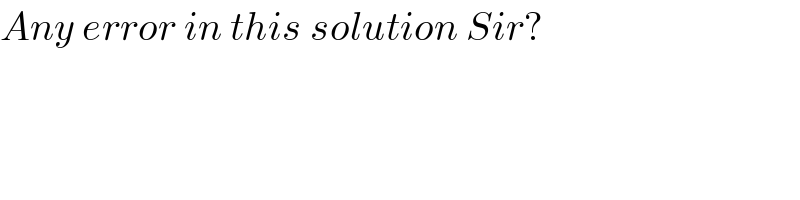
Any error in this solution Sir?
$${Any}\:{error}\:{in}\:{this}\:{solution}\:{Sir}? \\ $$
Commented by mr W last updated on 20/Nov/18
all correct sir!
$${all}\:{correct}\:{sir}! \\ $$
Answered by mr W last updated on 20/Nov/18
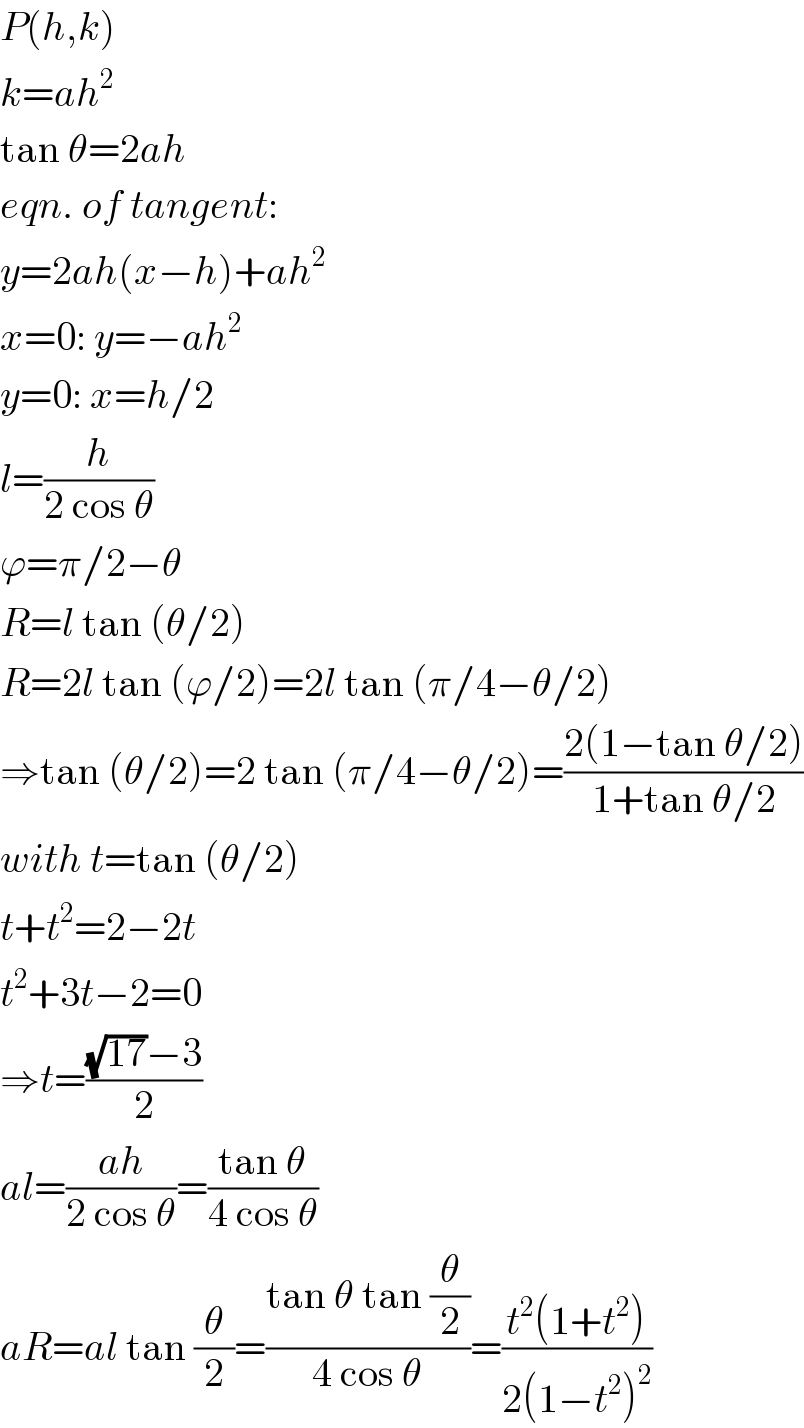
P(h,k) k=ah^2 tan θ=2ah eqn. of tangent: y=2ah(x−h)+ah^2 x=0: y=−ah^2 y=0: x=h/2 l=(h/(2 cos θ)) ϕ=π/2−θ R=l tan (θ/2) R=2l tan (ϕ/2)=2l tan (π/4−θ/2) ⇒tan (θ/2)=2 tan (π/4−θ/2)=((2(1−tan θ/2))/(1+tan θ/2)) with t=tan (θ/2) t+t^2 =2−2t t^2 +3t−2=0 ⇒t=(((√(17))−3)/2) al=((ah)/(2 cos θ))=((tan θ)/(4 cos θ)) aR=al tan (θ/2)=((tan θ tan (θ/2))/(4 cos θ))=((t^2 (1+t^2 ))/(2(1−t^2 )^2 ))
$${P}\left({h},{k}\right) \\ $$$${k}={ah}^{\mathrm{2}} \\ $$$$\mathrm{tan}\:\theta=\mathrm{2}{ah} \\ $$$${eqn}.\:{of}\:{tangent}: \\ $$$${y}=\mathrm{2}{ah}\left({x}−{h}\right)+{ah}^{\mathrm{2}} \\ $$$${x}=\mathrm{0}:\:{y}=−{ah}^{\mathrm{2}} \\ $$$${y}=\mathrm{0}:\:{x}={h}/\mathrm{2} \\ $$$${l}=\frac{{h}}{\mathrm{2}\:\mathrm{cos}\:\theta} \\ $$$$\varphi=\pi/\mathrm{2}−\theta \\ $$$${R}={l}\:\mathrm{tan}\:\left(\theta/\mathrm{2}\right) \\ $$$${R}=\mathrm{2}{l}\:\mathrm{tan}\:\left(\varphi/\mathrm{2}\right)=\mathrm{2}{l}\:\mathrm{tan}\:\left(\pi/\mathrm{4}−\theta/\mathrm{2}\right) \\ $$$$\Rightarrow\mathrm{tan}\:\left(\theta/\mathrm{2}\right)=\mathrm{2}\:\mathrm{tan}\:\left(\pi/\mathrm{4}−\theta/\mathrm{2}\right)=\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{tan}\:\theta/\mathrm{2}\right)}{\mathrm{1}+\mathrm{tan}\:\theta/\mathrm{2}} \\ $$$${with}\:{t}=\mathrm{tan}\:\left(\theta/\mathrm{2}\right) \\ $$$${t}+{t}^{\mathrm{2}} =\mathrm{2}−\mathrm{2}{t} \\ $$$${t}^{\mathrm{2}} +\mathrm{3}{t}−\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow{t}=\frac{\sqrt{\mathrm{17}}−\mathrm{3}}{\mathrm{2}} \\ $$$${al}=\frac{{ah}}{\mathrm{2}\:\mathrm{cos}\:\theta}=\frac{\mathrm{tan}\:\theta}{\mathrm{4}\:\mathrm{cos}\:\theta} \\ $$$${aR}={al}\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}=\frac{\mathrm{tan}\:\theta\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}{\mathrm{4}\:\mathrm{cos}\:\theta}=\frac{{t}^{\mathrm{2}} \left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{\mathrm{2}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$
Commented by ajfour last updated on 20/Nov/18
Its okay Sir, thank you.
$${Its}\:{okay}\:{Sir},\:{thank}\:{you}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *