Question Number 48182 by cesar.marval.larez@gmail.com last updated on 20/Nov/18
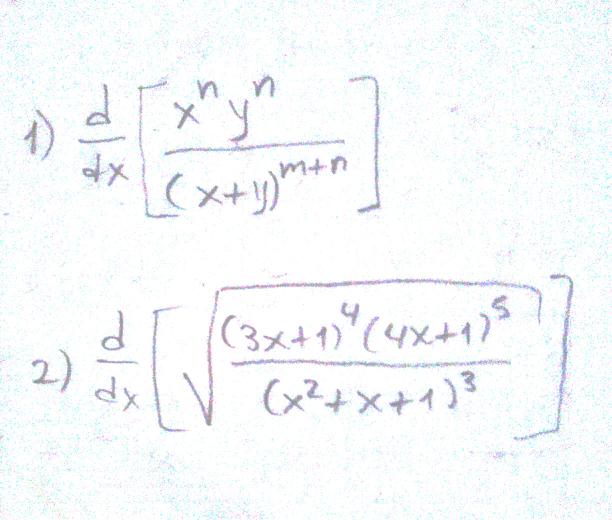
Answered by tanmay.chaudhury50@gmail.com last updated on 20/Nov/18
![1)t=((x^m y^n )/((x+y)^(m+n) )) lnt=mlnx+nlny−(m+n)ln(x+y) (1/t)(dt/dx)=(m/x)+(n/y)×(dy/dx)−((m+n)/(x+y))(1+(dy/dx)) (1/t)×(dt/dx)=(m/x)−((m+n)/(x+y))+(dy/dx)((n/y)−((m+n)/(x+y))) (dt/dx).=t[((mx+my−mx−nx)/(x(x+y)))+(dy/dx)(((nx+ny−my−ny)/(y(x+y)))] =((x^m y^n )/((x+y)^(m+n) ))[((my−nx)/(x(x+y)))−(dy/dx)(((my−nx)/(y(x+y)))] =((x^m y^n )/((x+y)^(m+n) ))×((my−nx)/(x+y))[(1/x)−(dy/dx)×(1/y)] 2)t=(√(((3x+1)^4 ×(4x+1)^5 )/((x^2 +x+1)^3 ))) lnt=(1/2)×[4ln(3x+1)+5ln(4x+1)−3ln(x^2 +x+1)] (1/t)×(dt/dx)=(1/2)[(4/(3x+1))×3+(5/(4x+1))×4−(3/(x^2 +x+1))×(2x+1)] (dt/dx)=(√(((3x+1)^4 ×(4x+1)^5 )/((x^2 +x+1)^3 ))) ×(1/2)[((12)/(3x+1))+((20)/(4x+1))−((3(2x+1))/((x^2 +x+1)^ ))]](https://www.tinkutara.com/question/Q48186.png)
$$\left.\mathrm{1}\right){t}=\frac{{x}^{{m}} {y}^{{n}} }{\left({x}+{y}\right)^{{m}+{n}} } \\ $$$${lnt}={mlnx}+{nlny}−\left({m}+{n}\right){ln}\left({x}+{y}\right) \\ $$$$\frac{\mathrm{1}}{{t}}\frac{{dt}}{{dx}}=\frac{{m}}{{x}}+\frac{{n}}{{y}}×\frac{{dy}}{{dx}}−\frac{{m}+{n}}{{x}+{y}}\left(\mathrm{1}+\frac{{dy}}{{dx}}\right) \\ $$$$\frac{\mathrm{1}}{{t}}×\frac{{dt}}{{dx}}=\frac{{m}}{{x}}−\frac{{m}+{n}}{{x}+{y}}+\frac{{dy}}{{dx}}\left(\frac{{n}}{{y}}−\frac{{m}+{n}}{{x}+{y}}\right) \\ $$$$\frac{{dt}}{{dx}}.={t}\left[\frac{{mx}+{my}−{mx}−{nx}}{{x}\left({x}+{y}\right)}+\frac{{dy}}{{dx}}\left(\frac{{nx}+{ny}−{my}−{ny}}{{y}\left({x}+{y}\right.}\right)\right] \\ $$$$ \\ $$$$=\frac{{x}^{{m}} {y}^{{n}} }{\left({x}+{y}\right)^{{m}+{n}} }\left[\frac{{my}−{nx}}{{x}\left({x}+{y}\right)}−\frac{{dy}}{{dx}}\left(\frac{{my}−{nx}}{{y}\left({x}+{y}\right)}\right]\right. \\ $$$$=\frac{{x}^{{m}} {y}^{{n}} }{\left({x}+{y}\right)^{{m}+{n}} }×\frac{{my}−{nx}}{{x}+{y}}\left[\frac{\mathrm{1}}{{x}}−\frac{{dy}}{{dx}}×\frac{\mathrm{1}}{{y}}\right] \\ $$$$\left.\mathrm{2}\right){t}=\sqrt{\frac{\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{4}} ×\left(\mathrm{4}{x}+\mathrm{1}\right)^{\mathrm{5}} }{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{3}} }}\: \\ $$$${lnt}=\frac{\mathrm{1}}{\mathrm{2}}×\left[\mathrm{4}{ln}\left(\mathrm{3}{x}+\mathrm{1}\right)+\mathrm{5}{ln}\left(\mathrm{4}{x}+\mathrm{1}\right)−\mathrm{3}{ln}\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)\right] \\ $$$$\frac{\mathrm{1}}{{t}}×\frac{{dt}}{{dx}}=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{4}}{\mathrm{3}{x}+\mathrm{1}}×\mathrm{3}+\frac{\mathrm{5}}{\mathrm{4}{x}+\mathrm{1}}×\mathrm{4}−\frac{\mathrm{3}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}×\left(\mathrm{2}{x}+\mathrm{1}\right)\right] \\ $$$$\frac{{dt}}{{dx}}=\sqrt{\frac{\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{4}} ×\left(\mathrm{4}{x}+\mathrm{1}\right)^{\mathrm{5}} }{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{3}} \:}}\:×\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{12}}{\mathrm{3}{x}+\mathrm{1}}+\frac{\mathrm{20}}{\mathrm{4}{x}+\mathrm{1}}−\frac{\mathrm{3}\left(\mathrm{2}{x}+\mathrm{1}\right)}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{} }\right] \\ $$
Commented by cesar.marval.larez@gmail.com last updated on 21/Nov/18

$${Thank}\:{u}\:{very}\:{much}\:{i}\:{am}\:{learning}\: \\ $$$${more}.\:{If}\:{i}\:{dont}\:{know}\:{some}\:{i}\:{post} \\ $$
