Menu Close

Question-48246

Tinku Tara 0 Comments
Pin




Question Number 48246 by ajfour last updated on 21/Nov/18
Commented by ajfour last updated on 21/Nov/18
Find a/b , if the ellipse parameters are even a and b.
$${Find}\:{a}/{b}\:,\:{if}\:{the}\:{ellipse}\:{parameters} \\ $$$${are}\:{even}\:{a}\:{and}\:{b}. \\ $$
Answered by mr W last updated on 21/Nov/18
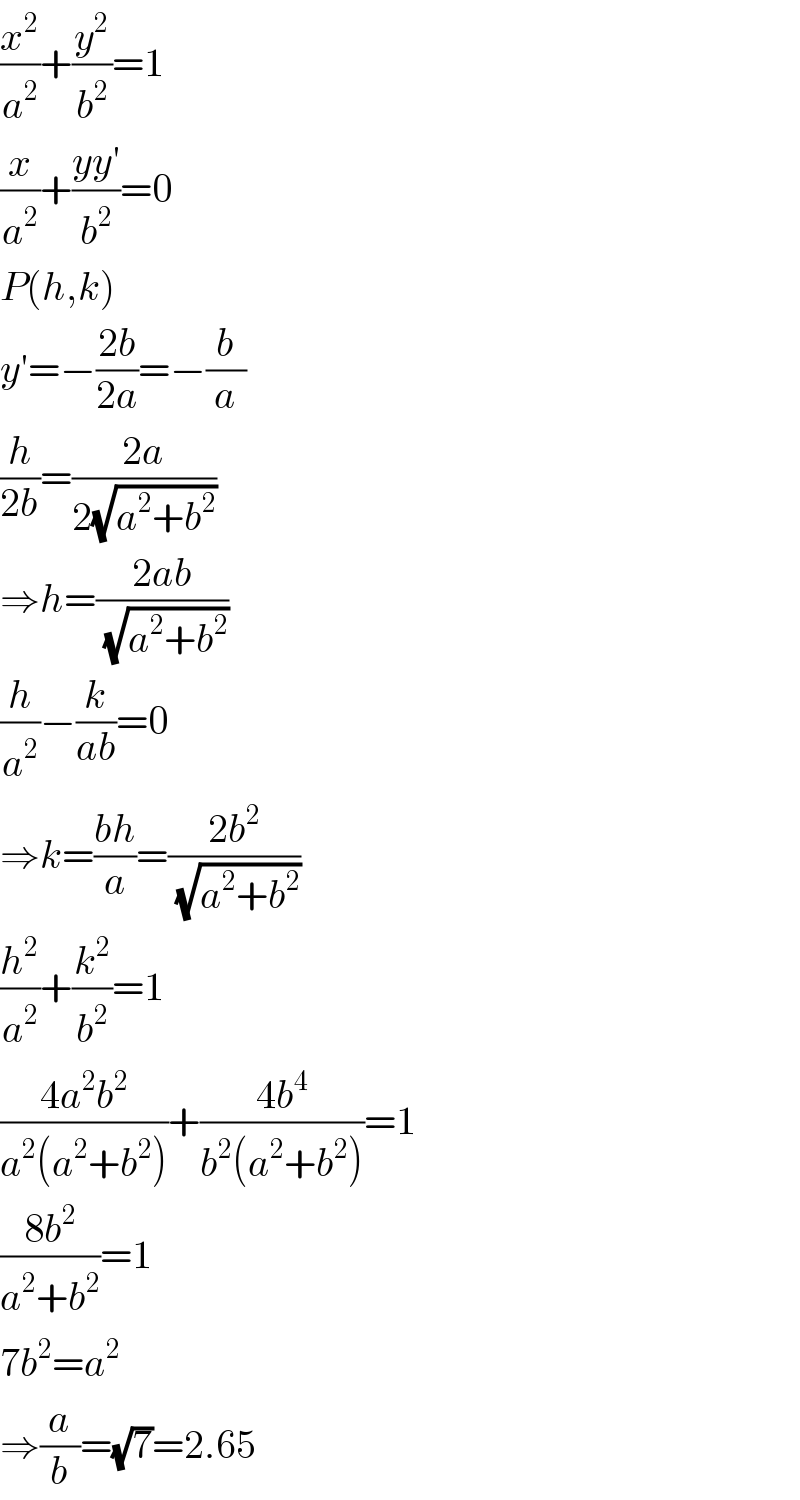
(x^2 /a^2 )+(y^2 /b^2 )=1 (x/a^2 )+((yy′)/b^2 )=0 P(h,k) y′=−((2b)/(2a))=−(b/a) (h/(2b))=((2a)/(2(√(a^2 +b^2 )))) ⇒h=((2ab)/( (√(a^2 +b^2 )))) (h/a^2 )−(k/(ab))=0 ⇒k=((bh)/a)=((2b^2 )/( (√(a^2 +b^2 )))) (h^2 /a^2 )+(k^2 /b^2 )=1 ((4a^2 b^2 )/(a^2 (a^2 +b^2 )))+((4b^4 )/(b^2 (a^2 +b^2 )))=1 ((8b^2 )/(a^2 +b^2 ))=1 7b^2 =a^2 ⇒(a/b)=(√7)=2.65
$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\frac{{x}}{{a}^{\mathrm{2}} }+\frac{{yy}'}{{b}^{\mathrm{2}} }=\mathrm{0} \\ $$$${P}\left({h},{k}\right) \\ $$$${y}'=−\frac{\mathrm{2}{b}}{\mathrm{2}{a}}=−\frac{{b}}{{a}} \\ $$$$\frac{{h}}{\mathrm{2}{b}}=\frac{\mathrm{2}{a}}{\mathrm{2}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$$$\Rightarrow{h}=\frac{\mathrm{2}{ab}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$$$\frac{{h}}{{a}^{\mathrm{2}} }−\frac{{k}}{{ab}}=\mathrm{0} \\ $$$$\Rightarrow{k}=\frac{{bh}}{{a}}=\frac{\mathrm{2}{b}^{\mathrm{2}} }{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$$$\frac{{h}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{k}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\frac{\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{a}^{\mathrm{2}} \left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)}+\frac{\mathrm{4}{b}^{\mathrm{4}} }{{b}^{\mathrm{2}} \left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)}=\mathrm{1} \\ $$$$\frac{\mathrm{8}{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\mathrm{7}{b}^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$$\Rightarrow\frac{{a}}{{b}}=\sqrt{\mathrm{7}}=\mathrm{2}.\mathrm{65} \\ $$
Commented by ajfour last updated on 21/Nov/18
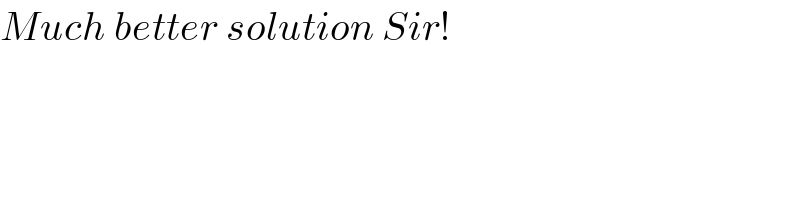
Much better solution Sir!
$${Much}\:{better}\:{solution}\:{Sir}! \\ $$
Answered by ajfour last updated on 21/Nov/18
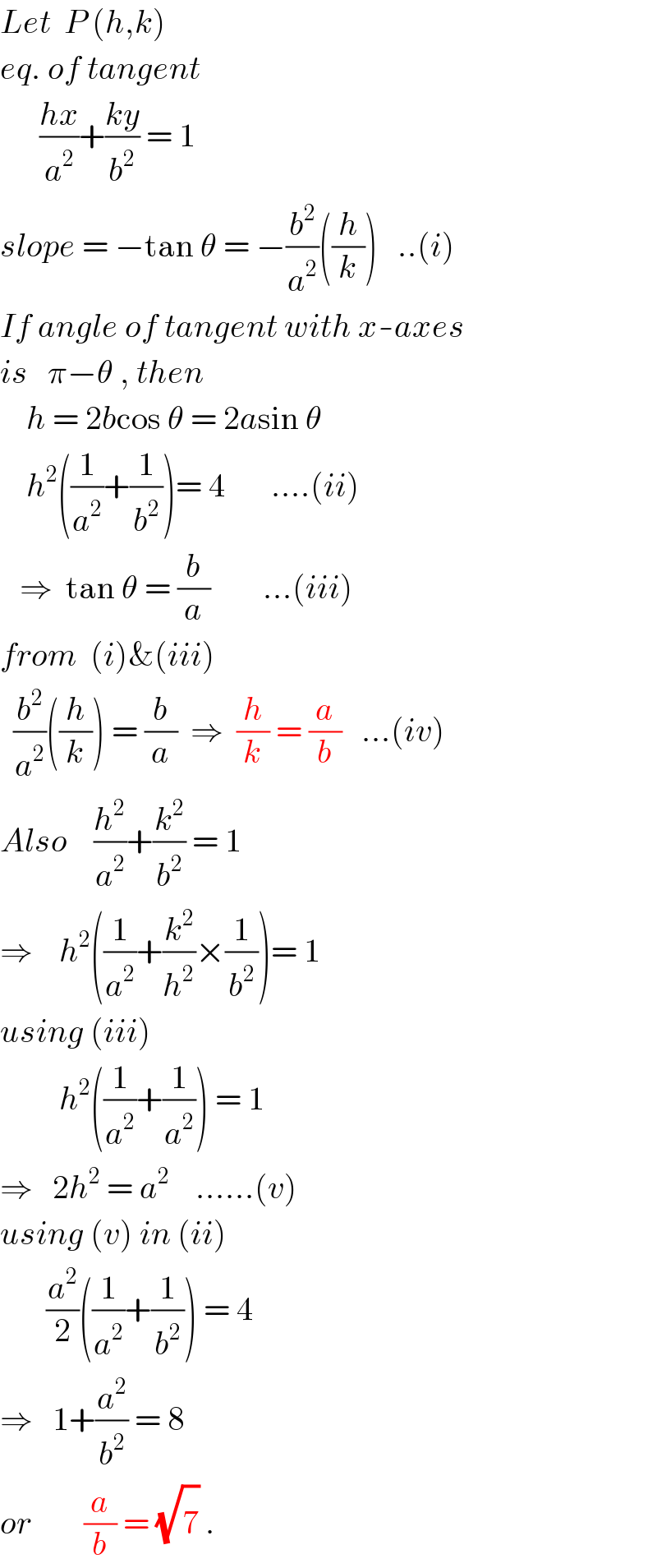
Let P (h,k) eq. of tangent ((hx)/a^2 )+((ky)/b^2 ) = 1 slope = −tan θ = −(b^2 /a^2 )((h/k)) ..(i) If angle of tangent with x-axes is π−θ , then h = 2bcos θ = 2asin θ h^2 ((1/a^2 )+(1/b^2 ))= 4 ....(ii) ⇒ tan θ = (b/a) ...(iii) from (i)&(iii) (b^2 /a^2 )((h/k)) = (b/a) ⇒ (h/k) = (a/b) ...(iv) Also (h^2 /a^2 )+(k^2 /b^2 ) = 1 ⇒ h^2 ((1/a^2 )+(k^2 /h^2 )×(1/b^2 ))= 1 using (iii) h^2 ((1/a^2 )+(1/a^2 )) = 1 ⇒ 2h^2 = a^2 ......(v) using (v) in (ii) (a^2 /2)((1/a^2 )+(1/b^2 )) = 4 ⇒ 1+(a^2 /b^2 ) = 8 or (a/b) = (√7^ ) .
$${Let}\:\:{P}\:\left({h},{k}\right) \\ $$$${eq}.\:{of}\:{tangent} \\ $$$$\:\:\:\:\:\:\frac{{hx}}{{a}^{\mathrm{2}} }+\frac{{ky}}{{b}^{\mathrm{2}} }\:=\:\mathrm{1} \\ $$$${slope}\:=\:−\mathrm{tan}\:\theta\:=\:−\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\left(\frac{{h}}{{k}}\right)\:\:\:..\left({i}\right) \\ $$$${If}\:{angle}\:{of}\:{tangent}\:{with}\:{x}-{axes} \\ $$$${is}\:\:\:\pi−\theta\:,\:{then} \\ $$$$\:\:\:\:{h}\:=\:\mathrm{2}{b}\mathrm{cos}\:\theta\:=\:\mathrm{2}{a}\mathrm{sin}\:\theta \\ $$$$\:\:\:\:{h}^{\mathrm{2}} \left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }\right)=\:\mathrm{4}\:\:\:\:\:\:\:….\left({ii}\right) \\ $$$$\:\:\:\Rightarrow\:\:\mathrm{tan}\:\theta\:=\:\frac{{b}}{{a}}\:\:\:\:\:\:\:\:…\left({iii}\right) \\ $$$${from}\:\:\left({i}\right)\&\left({iii}\right) \\ $$$$\:\:\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\left(\frac{{h}}{{k}}\right)\:=\:\frac{{b}}{{a}}\:\:\Rightarrow\:\:\frac{{h}}{{k}}\:=\:\frac{{a}}{{b}}\:\:\:…\left({iv}\right) \\ $$$${Also}\:\:\:\:\frac{{h}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{k}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\:=\:\mathrm{1} \\ $$$$\Rightarrow\:\:\:\:{h}^{\mathrm{2}} \left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{{k}^{\mathrm{2}} }{{h}^{\mathrm{2}} }×\frac{\mathrm{1}}{{b}^{\mathrm{2}} }\right)=\:\mathrm{1} \\ $$$${using}\:\left({iii}\right) \\ $$$$\:\:\:\:\:\:\:\:\:{h}^{\mathrm{2}} \left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\right)\:=\:\mathrm{1} \\ $$$$\Rightarrow\:\:\:\mathrm{2}{h}^{\mathrm{2}} \:=\:{a}^{\mathrm{2}} \:\:\:\:……\left({v}\right) \\ $$$${using}\:\left({v}\right)\:{in}\:\left({ii}\right) \\ $$$$\:\:\:\:\:\:\:\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }\right)\:=\:\mathrm{4} \\ $$$$\Rightarrow\:\:\:\mathrm{1}+\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\:=\:\mathrm{8} \\ $$$${or}\:\:\:\:\:\:\:\:\frac{{a}}{{b}}\:=\:\sqrt{\overset{} {\mathrm{7}}}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *