Question Number 48283 by naka3546 last updated on 21/Nov/18
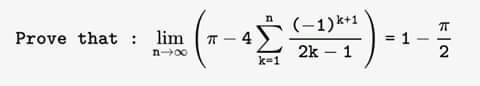
Commented by maxmathsup by imad last updated on 22/Nov/18
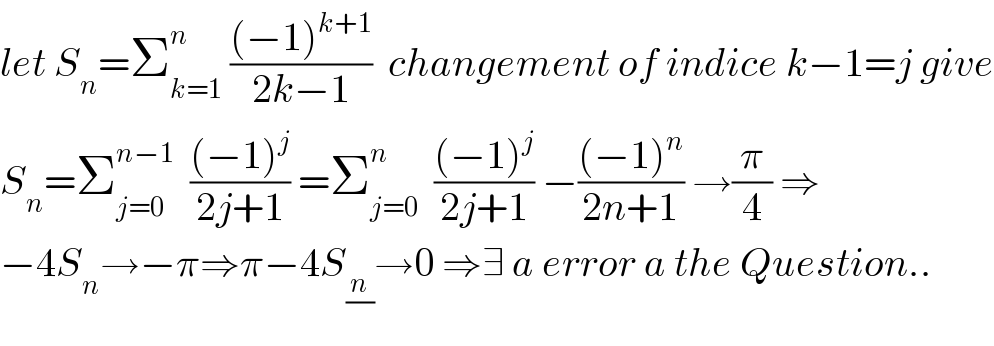
$${let}\:{S}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} }{\mathrm{2}{k}−\mathrm{1}}\:\:{changement}\:{of}\:{indice}\:{k}−\mathrm{1}={j}\:{give} \\ $$$${S}_{{n}} =\sum_{{j}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\frac{\left(−\mathrm{1}\right)^{{j}} }{\mathrm{2}{j}+\mathrm{1}}\:=\sum_{{j}=\mathrm{0}} ^{{n}} \:\:\frac{\left(−\mathrm{1}\right)^{{j}} }{\mathrm{2}{j}+\mathrm{1}}\:−\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}}\:\rightarrow\frac{\pi}{\mathrm{4}}\:\Rightarrow \\ $$$$−\mathrm{4}{S}_{{n}} \rightarrow−\pi\Rightarrow\pi−\mathrm{4}{S}_{\frac{{n}}{}} \rightarrow\mathrm{0}\:\Rightarrow\exists\:{a}\:{error}\:{a}\:{the}\:{Question}.. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 22/Nov/18

$${s}=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} }{\mathrm{2}{k}−\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}−…+\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\mathrm{2}{n}−\mathrm{1}} \\ $$$${if}\:{n}\rightarrow\infty \\ $$$${s}_{\infty} =\frac{\mathrm{1}}{\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}−…+\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\mathrm{2}{n}−\mathrm{1}}+…\infty \\ $$$${gregory}\:{series}… \\ $$$${tan}^{−\mathrm{1}} {x}={x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{{x}^{\mathrm{5}} }{\mathrm{5}}+… \\ $$$${put}\:{x}=\mathrm{1} \\ $$$$\frac{\pi}{\mathrm{4}}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{7}}+… \\ $$$${so}\:{answer}\:{is}\:{coming} \\ $$$$\pi−\mathrm{4}×\frac{\pi}{\mathrm{4}}=\mathrm{0} \\ $$
