Question Number 48396 by behi83417@gmail.com last updated on 23/Nov/18

Commented by MJS last updated on 23/Nov/18
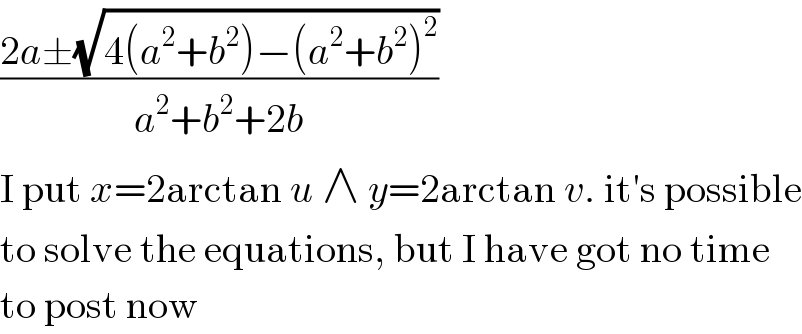
$$\frac{\mathrm{2}{a}\pm\sqrt{\mathrm{4}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)−\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\mathrm{2}} }}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{b}} \\ $$$$\mathrm{I}\:\mathrm{put}\:{x}=\mathrm{2arctan}\:{u}\:\wedge\:{y}=\mathrm{2arctan}\:{v}.\:\mathrm{it}'\mathrm{s}\:\mathrm{possible} \\ $$$$\mathrm{to}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{equations},\:\mathrm{but}\:\mathrm{I}\:\mathrm{have}\:\mathrm{got}\:\mathrm{no}\:\mathrm{time} \\ $$$$\mathrm{to}\:\mathrm{post}\:\mathrm{now} \\ $$
Commented by behi83417@gmail.com last updated on 23/Nov/18
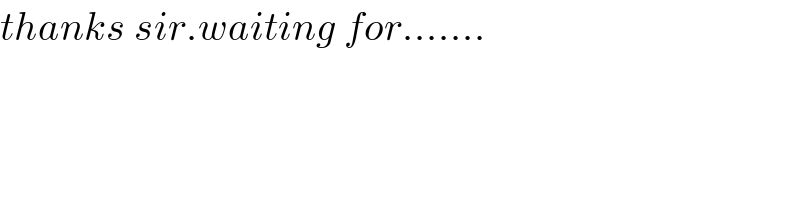
$${thanks}\:{sir}.{waiting}\:{for}……. \\ $$
Answered by ajfour last updated on 23/Nov/18
![s_1 ^2 +s_2 ^2 +2s_1 s_2 = a^2 c_1 ^2 +c_2 ^2 +2c_1 c_2 = b^2 ⇒ 2+2cos (x−y)= a^2 +b^2 ⇒ 4cos^2 (((x−y)/2))= a^2 +b^2 ⇒ 1+tan^2 (((x−y)/2))=(4/(a^2 +b^2 )) ⇒ x−y = 2tan^(−1) (√((4/(a^2 +b^2 ))−1)) .....(i) Also 2sin (((x+y)/2))cos (((x−y)/2))=a 2cos (((x+y)/2))cos (((x−y)/2))=b Dividing tan ((x+y)/2) = (a/b) ⇒ x+y = 2tan^(−1) (a/b) ....(ii) From (i) & (ii) tan (x/2) =tan [ (1/2)(tan^(−1) (a/b)+tan^(−1) (√((4/(a^2 +b^2 ))−1)) )] tan (y/2) =tan [ (1/2)(tan^(−1) (a/b)−tan^(−1) (√((4/(a^2 +b^2 ))−1)) )] _________________________ .](https://www.tinkutara.com/question/Q48408.png)
$${s}_{\mathrm{1}} ^{\mathrm{2}} +{s}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{2}{s}_{\mathrm{1}} {s}_{\mathrm{2}} \:=\:{a}^{\mathrm{2}} \\ $$$${c}_{\mathrm{1}} ^{\mathrm{2}} +{c}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{2}{c}_{\mathrm{1}} {c}_{\mathrm{2}} \:=\:{b}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{2}+\mathrm{2cos}\:\left({x}−{y}\right)=\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{4cos}\:^{\mathrm{2}} \left(\frac{{x}−{y}}{\mathrm{2}}\right)=\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \left(\frac{{x}−{y}}{\mathrm{2}}\right)=\frac{\mathrm{4}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:\:\: \\ $$$$\Rightarrow\:\:\:{x}−{y}\:=\:\mathrm{2tan}^{−\mathrm{1}} \sqrt{\frac{\mathrm{4}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…..\left({i}\right) \\ $$$${Also} \\ $$$$\:\:\:\:\:\mathrm{2sin}\:\left(\frac{{x}+{y}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{{x}−{y}}{\mathrm{2}}\right)={a} \\ $$$$\:\:\:\:\:\mathrm{2cos}\:\left(\frac{{x}+{y}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{{x}−{y}}{\mathrm{2}}\right)={b} \\ $$$${Dividing} \\ $$$$\:\:\:\:\:\mathrm{tan}\:\frac{{x}+{y}}{\mathrm{2}}\:=\:\frac{{a}}{{b}}\: \\ $$$$\Rightarrow\:\:\:{x}+{y}\:=\:\mathrm{2tan}^{−\mathrm{1}} \frac{{a}}{{b}}\:\:\:\:\:\:….\left({ii}\right) \\ $$$${From}\:\left({i}\right)\:\&\:\left({ii}\right) \\ $$$$\:\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:=\mathrm{tan}\:\left[\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{tan}^{−\mathrm{1}} \frac{{a}}{{b}}+\mathrm{tan}^{−\mathrm{1}} \sqrt{\frac{\mathrm{4}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }−\mathrm{1}}\:\right)\right] \\ $$$$\:\mathrm{tan}\:\frac{{y}}{\mathrm{2}}\:=\mathrm{tan}\:\left[\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{tan}^{−\mathrm{1}} \frac{{a}}{{b}}−\mathrm{tan}^{−\mathrm{1}} \sqrt{\frac{\mathrm{4}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }−\mathrm{1}}\:\right)\right] \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\:. \\ $$
Commented by behi83417@gmail.com last updated on 23/Nov/18
![[tg((x+y)/2)=(a/b),4cos^2 ((x−y)/2)=a^2 +b^2 ]⇒ { ((cos(( x−y)/2)=((√(a^2 +b^2 ))/2))),((cos(( x+y)/2)=(b/( (√(a^2 +b^2 )))))) :} ⇒ { ((2cos(x/2)cos(y/2)=((√(a^2 +b^2 ))/2)+(b/( (√(a^2 +b^2 ))))=((a^2 +b^2 +2b)/(2(√(a^2 +b^2 )))))),((2sin(x/2)sin(y/2)=((√(a^2 +b^2 ))/b)−(b/( (√(a^2 +b^2 ))))=((a^2 +b^2 −2b)/(2(√(a^2 +b^2 )))))) :} so: tg(( x)/2).tg(( y)/2)=((a^2 +b^2 −2b)/(a^2 +b^2 +2b)). and:tg(x/2)+tg(y/2)=tg((x+y)/2)(1−tg(x/2)tg(y/2))= =(a/b)(1−((a^2 +b^2 −2b)/(a^2 +b^2 +2b)))=((4a)/(a^2 +b^2 +2b)) i.e:tg(x/2) and tg(y/2),are the roots of: t^2 −((4a)/(a^2 +b^2 +2b))t+((a^2 +b^2 −2b)/(a^2 +b^2 +2b))=0 ⇒(a^2 +b^2 +2b)t−4at+(a^2 +b^2 −2b)=0 t=((2a±(√(4a^2 −[(a^2 +b^2 +2b)(a^2 +b^2 −2b))))/(a^2 +b^2 +2b))= =((2a±(√(4a^2 −[(a^2 +b^2 )^2 −4b^2 ])))/(a^2 +b^2 +2b))= =((2a±(√(4(a^2 +b^2 )−(a^2 +b^2 )^2 )))/(a^2 +b^2 +2b)) .](https://www.tinkutara.com/question/Q48431.png)
$$\left[{tg}\frac{{x}+{y}}{\mathrm{2}}=\frac{{a}}{{b}},\mathrm{4}{cos}^{\mathrm{2}} \frac{{x}−{y}}{\mathrm{2}}={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right]\Rightarrow \\ $$$$\begin{cases}{{cos}\frac{\:{x}−{y}}{\mathrm{2}}=\frac{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}{\mathrm{2}}}\\{{cos}\frac{\:{x}+{y}}{\mathrm{2}}=\frac{{b}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}}\end{cases} \\ $$$$\Rightarrow\begin{cases}{\mathrm{2}{cos}\frac{{x}}{\mathrm{2}}{cos}\frac{{y}}{\mathrm{2}}=\frac{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}{\mathrm{2}}+\frac{{b}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{b}}{\mathrm{2}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}}\\{\mathrm{2}{sin}\frac{{x}}{\mathrm{2}}{sin}\frac{{y}}{\mathrm{2}}=\frac{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}{{b}}−\frac{{b}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{b}}{\mathrm{2}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}}\end{cases} \\ $$$${so}:\:\boldsymbol{\mathrm{tg}}\frac{\:\boldsymbol{\mathrm{x}}}{\mathrm{2}}.\boldsymbol{\mathrm{tg}}\frac{\:\boldsymbol{\mathrm{y}}}{\mathrm{2}}=\frac{\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{\mathrm{b}}}{\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} +\mathrm{2}\boldsymbol{\mathrm{b}}}. \\ $$$${and}:\boldsymbol{\mathrm{tg}}\frac{\boldsymbol{\mathrm{x}}}{\mathrm{2}}+\boldsymbol{\mathrm{tg}}\frac{\boldsymbol{\mathrm{y}}}{\mathrm{2}}=\boldsymbol{\mathrm{tg}}\frac{\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}}{\mathrm{2}}\left(\mathrm{1}−\boldsymbol{\mathrm{tg}}\frac{\boldsymbol{\mathrm{x}}}{\mathrm{2}}\boldsymbol{\mathrm{tg}}\frac{\boldsymbol{\mathrm{y}}}{\mathrm{2}}\right)= \\ $$$$=\frac{\boldsymbol{\mathrm{a}}}{\boldsymbol{\mathrm{b}}}\left(\mathrm{1}−\frac{\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{\mathrm{b}}}{\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} +\mathrm{2}\boldsymbol{\mathrm{b}}}\right)=\frac{\mathrm{4}\boldsymbol{\mathrm{a}}}{\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} +\mathrm{2}\boldsymbol{\mathrm{b}}} \\ $$$$\boldsymbol{\mathrm{i}}.\boldsymbol{\mathrm{e}}:{tg}\frac{{x}}{\mathrm{2}}\:{and}\:{tg}\frac{{y}}{\mathrm{2}},{are}\:{the}\:{roots}\:{of}: \\ $$$$\boldsymbol{\mathrm{t}}^{\mathrm{2}} −\frac{\mathrm{4}\boldsymbol{\mathrm{a}}}{\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} +\mathrm{2}\boldsymbol{\mathrm{b}}}\boldsymbol{\mathrm{t}}+\frac{\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{\mathrm{b}}}{\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} +\mathrm{2}\boldsymbol{\mathrm{b}}}=\mathrm{0} \\ $$$$\Rightarrow\left(\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} +\mathrm{2}\boldsymbol{\mathrm{b}}\right)\boldsymbol{\mathrm{t}}−\mathrm{4}\boldsymbol{\mathrm{at}}+\left(\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{\mathrm{b}}\right)=\mathrm{0} \\ $$$${t}=\frac{\mathrm{2}{a}\pm\sqrt{\mathrm{4}{a}^{\mathrm{2}} −\left[\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{b}\right)\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{b}\right)\right.}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{b}}= \\ $$$$=\frac{\mathrm{2}{a}\pm\sqrt{\mathrm{4}{a}^{\mathrm{2}} −\left[\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{4}{b}^{\mathrm{2}} \right]}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{b}}= \\ $$$$=\frac{\mathrm{2}{a}\pm\sqrt{\mathrm{4}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)−\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\mathrm{2}} }}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{b}}\:. \\ $$
Answered by MJS last updated on 23/Nov/18

$${x}=\mathrm{2arctan}\:{u} \\ $$$${y}=\mathrm{2arctan}\:{v} \\ $$$$\left(\mathrm{1}\right)\:\frac{\mathrm{2}\left({u}+{v}\right)\left({uv}+\mathrm{1}\right)}{\left({u}^{\mathrm{2}} +\mathrm{1}\right)\left({v}^{\mathrm{2}} +\mathrm{1}\right)}={a} \\ $$$$\left(\mathrm{2}\right)\:\frac{\mathrm{2}\left({uv}−\mathrm{1}\right)\left({uv}+\mathrm{1}\right)}{\left({u}^{\mathrm{2}} +\mathrm{1}\right)\left({v}^{\mathrm{2}} +\mathrm{1}\right)}={b} \\ $$$$\left(\mathrm{1}\right)\:{u}^{\mathrm{2}} =\frac{\mathrm{2}{uv}^{\mathrm{2}} +\mathrm{2}{u}−{av}^{\mathrm{2}} +\mathrm{2}{v}−{a}}{{av}^{\mathrm{2}} −\mathrm{2}{v}+{a}} \\ $$$$\left(\mathrm{2}\right)\:{u}^{\mathrm{2}} =\frac{\mathrm{2}−{b}−{bv}^{\mathrm{2}} }{\left({b}+\mathrm{2}\right){v}^{\mathrm{2}} +{b}} \\ $$$$\left(\mathrm{1}\right)−\left(\mathrm{2}\right)\:\Rightarrow\:{u}=\frac{{av}^{\mathrm{2}} −\mathrm{2}{v}+{a}}{\left({b}+\mathrm{2}\right){v}^{\mathrm{2}} +{b}} \\ $$$$\mathrm{using}\:\mathrm{this}\:\mathrm{in}\:\left(\mathrm{2}\right)\:\mathrm{we}\:\mathrm{get} \\ $$$${v}^{\mathrm{4}} −\frac{\mathrm{4}{a}}{{a}^{\mathrm{2}} +{b}\left({b}+\mathrm{2}\right)}{v}^{\mathrm{3}} +\frac{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)}{{a}^{\mathrm{2}} +{b}\left({b}+\mathrm{2}\right)}{v}^{\mathrm{2}} −\frac{\mathrm{4}{a}}{{a}^{\mathrm{2}} +{b}\left({b}+\mathrm{2}\right)}{v}+\frac{{a}^{\mathrm{2}} +{b}\left({b}−\mathrm{2}\right)}{{a}^{\mathrm{2}} +{b}\left({b}+\mathrm{2}\right)}=\mathrm{0} \\ $$$$\mathrm{now}\:\mathrm{this}\:\mathrm{is}\:\mathrm{what}\:\mathrm{I}\:\mathrm{found}: \\ $$$$\mathrm{1}−\frac{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)}{{a}^{\mathrm{2}} +{b}\left({b}+\mathrm{2}\right)}=−\frac{{a}^{\mathrm{2}} +{b}\left({b}−\mathrm{2}\right)}{{a}^{\mathrm{2}} +{b}\left({b}+\mathrm{2}\right)} \\ $$$$\Rightarrow\:\pm\mathrm{i}\:\mathrm{solves}\:\mathrm{above}\:\mathrm{equation}\:\Rightarrow \\ $$$$\left({v}^{\mathrm{2}} +\mathrm{1}\right)\left({v}^{\mathrm{2}} −\frac{\mathrm{4}{a}}{{a}^{\mathrm{2}} +{b}\left({b}+\mathrm{2}\right)}{v}+\frac{{a}^{\mathrm{2}} +{b}\left({b}−\mathrm{2}\right)}{{a}^{\mathrm{2}} +{b}\left({b}+\mathrm{2}\right)}\right)=\mathrm{0} \\ $$$$\mathrm{which}\:\mathrm{leads}\:\mathrm{to}\:\mathrm{the}\:\mathrm{posted}\:\mathrm{solution} \\ $$
