Menu Close

Question-48434

Tinku Tara 0 Comments
Pin




Question Number 48434 by behi83417@gmail.com last updated on 23/Nov/18
Answered by tanmay.chaudhury50@gmail.com last updated on 23/Nov/18
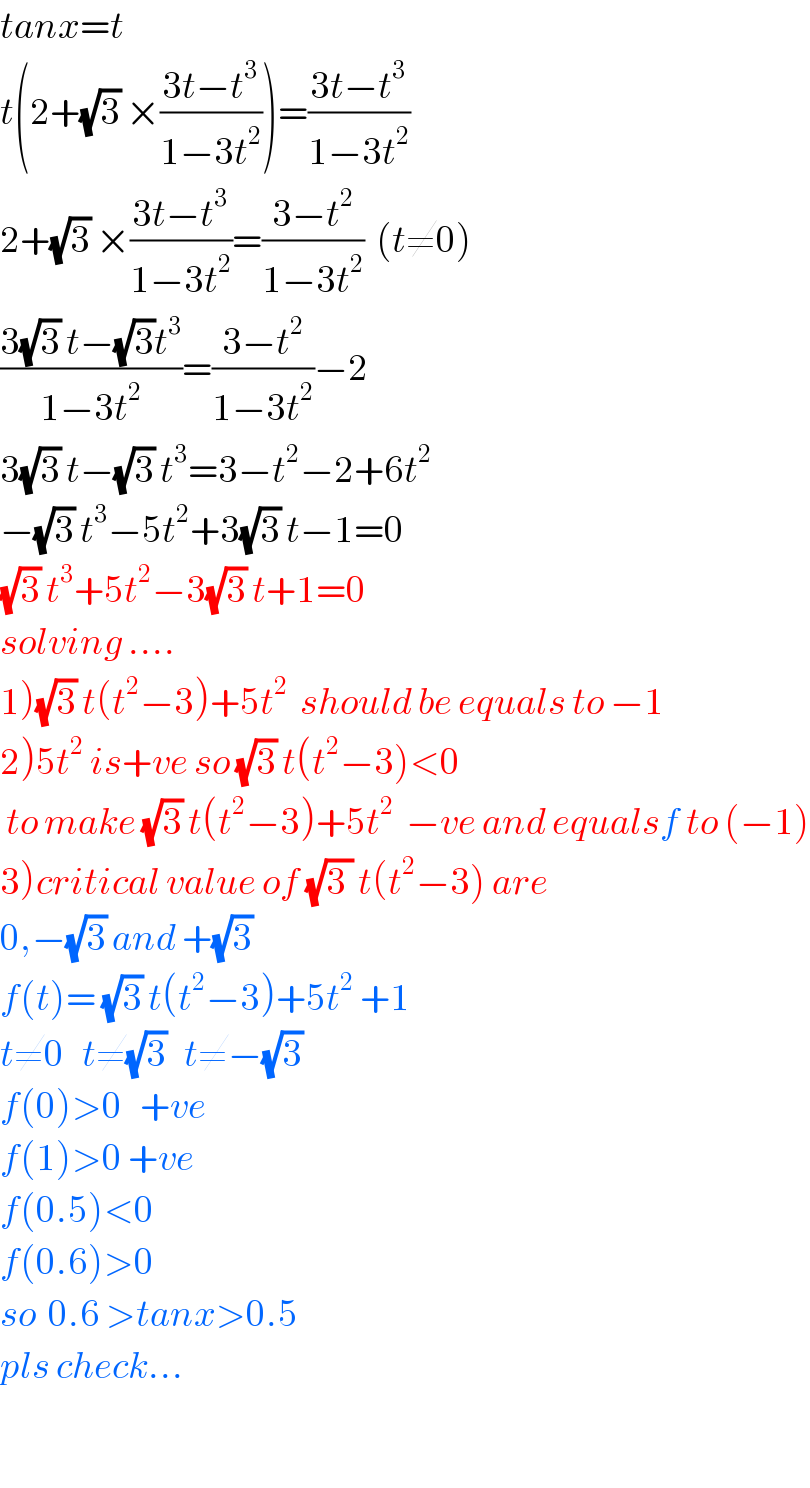
tanx=t t(2+(√3) ×((3t−t^3 )/(1−3t^2 )))=((3t−t^3 )/(1−3t^2 )) 2+(√3) ×((3t−t^3 )/(1−3t^2 ))=((3−t^2 )/(1−3t^2 )) (t≠0) ((3(√3) t−(√3)t^3 )/(1−3t^2 ))=((3−t^2 )/(1−3t^2 ))−2 3(√3) t−(√3) t^3 =3−t^2 −2+6t^2 −(√3) t^3 −5t^2 +3(√3) t−1=0 (√3) t^3 +5t^2 −3(√3) t+1=0 solving .... 1)(√3) t(t^2 −3)+5t^2 should be equals to −1 2)5t^2 is+ve so (√3) t(t^2 −3)<0 to make (√3) t(t^2 −3)+5t^2 −ve and equalsf to (−1) 3)critical value of (√(3 )) t(t^2 −3) are 0,−(√3) and +(√3) f(t)= (√3) t(t^2 −3)+5t^2 +1 t≠0 t≠(√3) t≠−(√3) f(0)>0 +ve f(1)>0 +ve f(0.5)<0 f(0.6)>0 so 0.6 >tanx>0.5 pls check...
$${tanx}={t} \\ $$$${t}\left(\mathrm{2}+\sqrt{\mathrm{3}}\:×\frac{\mathrm{3}{t}−{t}^{\mathrm{3}} }{\mathrm{1}−\mathrm{3}{t}^{\mathrm{2}} }\right)=\frac{\mathrm{3}{t}−{t}^{\mathrm{3}} }{\mathrm{1}−\mathrm{3}{t}^{\mathrm{2}} } \\ $$$$\mathrm{2}+\sqrt{\mathrm{3}}\:×\frac{\mathrm{3}{t}−{t}^{\mathrm{3}} }{\mathrm{1}−\mathrm{3}{t}^{\mathrm{2}} }=\frac{\mathrm{3}−{t}^{\mathrm{2}} }{\mathrm{1}−\mathrm{3}{t}^{\mathrm{2}} }\:\:\left({t}\neq\mathrm{0}\right) \\ $$$$\frac{\mathrm{3}\sqrt{\mathrm{3}}\:{t}−\sqrt{\mathrm{3}}{t}^{\mathrm{3}} }{\mathrm{1}−\mathrm{3}{t}^{\mathrm{2}} }=\frac{\mathrm{3}−{t}^{\mathrm{2}} }{\mathrm{1}−\mathrm{3}{t}^{\mathrm{2}} }−\mathrm{2} \\ $$$$\mathrm{3}\sqrt{\mathrm{3}}\:{t}−\sqrt{\mathrm{3}}\:{t}^{\mathrm{3}} =\mathrm{3}−{t}^{\mathrm{2}} −\mathrm{2}+\mathrm{6}{t}^{\mathrm{2}} \\ $$$$−\sqrt{\mathrm{3}}\:{t}^{\mathrm{3}} −\mathrm{5}{t}^{\mathrm{2}} +\mathrm{3}\sqrt{\mathrm{3}}\:{t}−\mathrm{1}=\mathrm{0} \\ $$$$\sqrt{\mathrm{3}}\:{t}^{\mathrm{3}} +\mathrm{5}{t}^{\mathrm{2}} −\mathrm{3}\sqrt{\mathrm{3}}\:{t}+\mathrm{1}=\mathrm{0} \\ $$$${solving}\:…. \\ $$$$\left.\mathrm{1}\right)\sqrt{\mathrm{3}}\:{t}\left({t}^{\mathrm{2}} −\mathrm{3}\right)+\mathrm{5}{t}^{\mathrm{2}} \:\:{should}\:{be}\:{equals}\:{to}\:−\mathrm{1} \\ $$$$\left.\mathrm{2}\right)\mathrm{5}{t}^{\mathrm{2}} \:{is}+{ve}\:{so}\:\sqrt{\mathrm{3}}\:{t}\left({t}^{\mathrm{2}} −\mathrm{3}\right)<\mathrm{0} \\ $$$$\:{to}\:{make}\:\sqrt{\mathrm{3}}\:{t}\left({t}^{\mathrm{2}} −\mathrm{3}\right)+\mathrm{5}{t}^{\mathrm{2}} \:\:−{ve}\:{and}\:{equalsf}\:{to}\:\left(−\mathrm{1}\right) \\ $$$$\left.\mathrm{3}\right){critical}\:{value}\:{of}\:\sqrt{\mathrm{3}\:}\:{t}\left({t}^{\mathrm{2}} −\mathrm{3}\right)\:{are} \\ $$$$\mathrm{0},−\sqrt{\mathrm{3}}\:{and}\:+\sqrt{\mathrm{3}}\: \\ $$$${f}\left({t}\right)=\:\sqrt{\mathrm{3}}\:{t}\left({t}^{\mathrm{2}} −\mathrm{3}\right)+\mathrm{5}{t}^{\mathrm{2}} \:+\mathrm{1} \\ $$$${t}\neq\mathrm{0}\:\:\:{t}\neq\sqrt{\mathrm{3}}\:\:\:{t}\neq−\sqrt{\mathrm{3}}\: \\ $$$${f}\left(\mathrm{0}\right)>\mathrm{0}\:\:\:+{ve} \\ $$$${f}\left(\mathrm{1}\right)>\mathrm{0}\:+{ve} \\ $$$${f}\left(\mathrm{0}.\mathrm{5}\right)<\mathrm{0} \\ $$$${f}\left(\mathrm{0}.\mathrm{6}\right)>\mathrm{0} \\ $$$${so}\:\:\mathrm{0}.\mathrm{6}\:>{tanx}>\mathrm{0}.\mathrm{5} \\ $$$${pls}\:{check}… \\ $$$$ \\ $$
Commented by behi83417@gmail.com last updated on 24/Nov/18
thank you very much sir.
$${thank}\:{you}\:{very}\:{much}\:{sir}. \\ $$
Answered by MJS last updated on 23/Nov/18
x=arctan t (((√3)t^4 +5t^3 −3(√3)t^2 +t)/(3t^2 −1))=0 ⇒ 3t^2 −1≠0 ⇒ t≠±((√3)/3) t((√3)t^3 +5t^2 −3(√3)t+1)=0 ⇒ t_1 =0 ⇒ x_1 =0 t^3 +((5(√3))/3)t^2 −3t+((√3)/3)=0 trying t=±((√3)/3) ⇒ t_2 =((√3)/3) but t≠((√3)/3) ⇒ no solution of given eq t^2 +2(√3)t−1=0 ⇒ t_3 =−2−(√3); t_4 =2−(√3) ⇒ x_3 =−((5π)/(12)); x_4 =(π/(12)) answer is (x=zπ∨x=−((5π)/(12))+zπ∨x=(π/(12))+zπ)∧z∈Z
$${x}=\mathrm{arctan}\:{t} \\ $$$$\frac{\sqrt{\mathrm{3}}{t}^{\mathrm{4}} +\mathrm{5}{t}^{\mathrm{3}} −\mathrm{3}\sqrt{\mathrm{3}}{t}^{\mathrm{2}} +{t}}{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{1}}=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{3}{t}^{\mathrm{2}} −\mathrm{1}\neq\mathrm{0}\:\Rightarrow\:{t}\neq\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$$${t}\left(\sqrt{\mathrm{3}}{t}^{\mathrm{3}} +\mathrm{5}{t}^{\mathrm{2}} −\mathrm{3}\sqrt{\mathrm{3}}{t}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\:{t}_{\mathrm{1}} =\mathrm{0}\:\Rightarrow\:{x}_{\mathrm{1}} =\mathrm{0} \\ $$$${t}^{\mathrm{3}} +\frac{\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{3}}{t}^{\mathrm{2}} −\mathrm{3}{t}+\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}=\mathrm{0} \\ $$$$\mathrm{trying}\:{t}=\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\:\Rightarrow\:{t}_{\mathrm{2}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\:\mathrm{but}\:{t}\neq\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\:\Rightarrow\:\mathrm{no}\:\mathrm{solution}\:\mathrm{of}\:\mathrm{given}\:\mathrm{eq} \\ $$$${t}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{3}}{t}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:{t}_{\mathrm{3}} =−\mathrm{2}−\sqrt{\mathrm{3}};\:{t}_{\mathrm{4}} =\mathrm{2}−\sqrt{\mathrm{3}} \\ $$$$\Rightarrow\:{x}_{\mathrm{3}} =−\frac{\mathrm{5}\pi}{\mathrm{12}};\:{x}_{\mathrm{4}} =\frac{\pi}{\mathrm{12}} \\ $$$$\mathrm{answer}\:\mathrm{is} \\ $$$$\left({x}={z}\pi\vee{x}=−\frac{\mathrm{5}\pi}{\mathrm{12}}+{z}\pi\vee{x}=\frac{\pi}{\mathrm{12}}+{z}\pi\right)\wedge{z}\in\mathbb{Z} \\ $$
Commented by behi83417@gmail.com last updated on 24/Nov/18
thanks in advance sir.
$${thanks}\:{in}\:{advance}\:{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *