Question-48458

Question Number 48458 by ajfour last updated on 24/Nov/18

Commented by ajfour last updated on 24/Nov/18

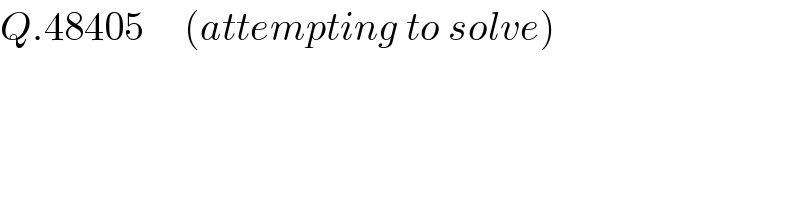
$${Q}.\mathrm{48405}\:\:\:\:\:\left({attempting}\:{to}\:{solve}\right) \\ $$

Answered by ajfour last updated on 24/Nov/18

let θ in figure be dθ. Then 2Tdθ = E_0 dQ ⇒ 2Tdθ = E_0 ((Q/(2πR)))(2dθ) or T = ((E_0 Q)/(2πR)) ......(i) And for E_0 _(−) dE_0 = ((dqcos (φ/2))/(4πε_0 x^2 )) x is distance from dq to center of dQ ; x = 2Rcos (φ/2) E_0 (due to charge from θ to 2π−θ) = 2∫_0 ^( π−θ) (((λRdφ)(cos (φ/2)))/(4πε_0 (4R^2 cos^2 (φ/2)))) = (λ/(4πε_0 R)) ∫_0 ^( (π/2)−(θ/2)) (sec (φ/2))d((φ/2)) = (λ/(4πε_0 R)) ln ∣sec ((π/2)−(θ/2))+tan ((π/2)−(θ/2))∣ = (λ/(4πε_0 R)) ln ∣(1/(sin (θ/2)))+((cos (θ/2))/(sin (θ/2)))∣ =(λ/(4πε_0 R)) ln (cot (θ/4)) Still this will not be helpful; very difficult question..

$${let}\:\theta\:{in}\:{figure}\:{be}\:{d}\theta. \\ $$$${Then}\:\:\mathrm{2}{Td}\theta\:=\:{E}_{\mathrm{0}} {dQ} \\ $$$$\Rightarrow\:\:\mathrm{2}{Td}\theta\:=\:{E}_{\mathrm{0}} \left(\frac{{Q}}{\mathrm{2}\pi{R}}\right)\left(\mathrm{2}{d}\theta\right) \\ $$$${or}\:\:\:\:{T}\:=\:\frac{{E}_{\mathrm{0}} {Q}}{\mathrm{2}\pi{R}}\:\:\:\:\:\:\:\:\:\:\:……\left({i}\right) \\ $$$$\underset{−} {{And}\:{for}\:{E}_{\mathrm{0}} } \\ $$$$\:\:\:{dE}_{\mathrm{0}} \:=\:\frac{{dq}\mathrm{cos}\:\frac{\phi}{\mathrm{2}}}{\mathrm{4}\pi\epsilon_{\mathrm{0}} {x}^{\mathrm{2}} } \\ $$$$\:\:{x}\:{is}\:{distance}\:{from}\:{dq}\:{to}\:{center} \\ $$$${of}\:{dQ}\:; \\ $$$$\:\:\:\:\:\:\:{x}\:=\:\mathrm{2}{R}\mathrm{cos}\:\frac{\phi}{\mathrm{2}} \\ $$$$\:\:\:{E}_{\mathrm{0}} \left({due}\:{to}\:{charge}\:{from}\:\theta\:{to}\:\mathrm{2}\pi−\theta\right)\: \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:\mathrm{2}\int_{\mathrm{0}} ^{\:\:\pi−\theta} \:\frac{\left(\lambda{Rd}\phi\right)\left(\mathrm{cos}\:\frac{\phi}{\mathrm{2}}\right)}{\mathrm{4}\pi\epsilon_{\mathrm{0}} \left(\mathrm{4}{R}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \frac{\phi}{\mathrm{2}}\right)} \\ $$$$\:\:\:\:=\:\frac{\lambda}{\mathrm{4}\pi\epsilon_{\mathrm{0}} {R}}\:\int_{\mathrm{0}} ^{\:\:\frac{\pi}{\mathrm{2}}−\frac{\theta}{\mathrm{2}}} \left(\mathrm{sec}\:\frac{\phi}{\mathrm{2}}\right){d}\left(\frac{\phi}{\mathrm{2}}\right)\: \\ $$$$\:\:\:=\:\frac{\lambda}{\mathrm{4}\pi\epsilon_{\mathrm{0}} {R}}\:\mathrm{ln}\:\mid\mathrm{sec}\:\left(\frac{\pi}{\mathrm{2}}−\frac{\theta}{\mathrm{2}}\right)+\mathrm{tan}\:\left(\frac{\pi}{\mathrm{2}}−\frac{\theta}{\mathrm{2}}\right)\mid \\ $$$$\:\:\:=\:\frac{\lambda}{\mathrm{4}\pi\epsilon_{\mathrm{0}} {R}}\:\mathrm{ln}\:\mid\frac{\mathrm{1}}{\mathrm{sin}\:\frac{\theta}{\mathrm{2}}}+\frac{\mathrm{cos}\:\frac{\theta}{\mathrm{2}}}{\mathrm{sin}\:\frac{\theta}{\mathrm{2}}}\mid \\ $$$$\:\:=\frac{\lambda}{\mathrm{4}\pi\epsilon_{\mathrm{0}} {R}}\:\:\mathrm{ln}\:\left(\mathrm{cot}\:\frac{\theta}{\mathrm{4}}\right) \\ $$$$\:\:\:{Still}\:{this}\:{will}\:{not}\:{be}\:{helpful}; \\ $$$$\:\:\:\:\:{very}\:{difficult}\:{question}.. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply