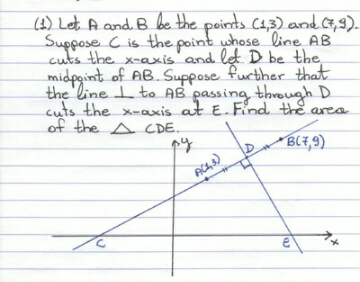
Question Number 48466 by Tawa1 last updated on 24/Nov/18
Answered by tanmay.chaudhury50@gmail.com last updated on 24/Nov/18
![A(1,3) B(7,9) D(4,6) eqn AB (y−3)=((9−3)/(7−1))(x−1) y−3−x+1=0 y−x−2=0 point C(−2,0) eqn DE (y−6)=(−1)(x−4) y−6+x−4=0 y+x−10=0 point E(10,0) in triangle △CDE C(−2,0) D(4,6) E(10,0) area =(1/2)[x_1 (y_2 −y_3 )+x_2 (y_3 −y_1 )+x_3 (y_1 −y_2 )] =(1/2)[(−2)(6−0)+4(0−0)+10(0−6)] =(1/2)[−12−60]=−36 so area is 36 unit](https://www.tinkutara.com/question/Q48467.png)
$${A}\left(\mathrm{1},\mathrm{3}\right)\:\:{B}\left(\mathrm{7},\mathrm{9}\right)\:\:\:{D}\left(\mathrm{4},\mathrm{6}\right) \\ $$$${eqn}\:{AB}\:\:\left({y}−\mathrm{3}\right)=\frac{\mathrm{9}−\mathrm{3}}{\mathrm{7}−\mathrm{1}}\left({x}−\mathrm{1}\right) \\ $$$${y}−\mathrm{3}−{x}+\mathrm{1}=\mathrm{0} \\ $$$${y}−{x}−\mathrm{2}=\mathrm{0} \\ $$$${point}\:{C}\left(−\mathrm{2},\mathrm{0}\right) \\ $$$${eqn}\:{DE}\:\:\left({y}−\mathrm{6}\right)=\left(−\mathrm{1}\right)\left({x}−\mathrm{4}\right) \\ $$$${y}−\mathrm{6}+{x}−\mathrm{4}=\mathrm{0} \\ $$$${y}+{x}−\mathrm{10}=\mathrm{0} \\ $$$${point}\:{E}\left(\mathrm{10},\mathrm{0}\right) \\ $$$${in}\:{triangle}\:\bigtriangleup{CDE}\:\:{C}\left(−\mathrm{2},\mathrm{0}\right)\:\:{D}\left(\mathrm{4},\mathrm{6}\right)\:\:{E}\left(\mathrm{10},\mathrm{0}\right) \\ $$$${area}\:=\frac{\mathrm{1}}{\mathrm{2}}\left[{x}_{\mathrm{1}} \left({y}_{\mathrm{2}} −{y}_{\mathrm{3}} \right)+{x}_{\mathrm{2}} \left({y}_{\mathrm{3}} −{y}_{\mathrm{1}} \right)+{x}_{\mathrm{3}} \left({y}_{\mathrm{1}} −{y}_{\mathrm{2}} \right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\left(−\mathrm{2}\right)\left(\mathrm{6}−\mathrm{0}\right)+\mathrm{4}\left(\mathrm{0}−\mathrm{0}\right)+\mathrm{10}\left(\mathrm{0}−\mathrm{6}\right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[−\mathrm{12}−\mathrm{60}\right]=−\mathrm{36} \\ $$$$ \\ $$$${so}\:{area}\:{is}\:\mathrm{36}\:{unit} \\ $$
Commented by $@ty@m last updated on 24/Nov/18
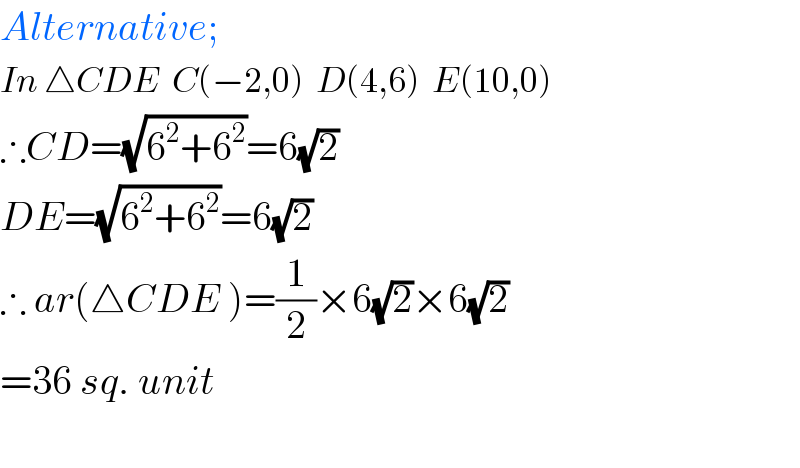
$${Alternative}; \\ $$$${In}\:\bigtriangleup{CDE}\:\:{C}\left(−\mathrm{2},\mathrm{0}\right)\:\:{D}\left(\mathrm{4},\mathrm{6}\right)\:\:{E}\left(\mathrm{10},\mathrm{0}\right) \\ $$$$\therefore{CD}=\sqrt{\mathrm{6}^{\mathrm{2}} +\mathrm{6}^{\mathrm{2}} }=\mathrm{6}\sqrt{\mathrm{2}} \\ $$$${DE}=\sqrt{\mathrm{6}^{\mathrm{2}} +\mathrm{6}^{\mathrm{2}} }=\mathrm{6}\sqrt{\mathrm{2}} \\ $$$$\therefore\:{ar}\left(\bigtriangleup{CDE}\:\right)=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{6}\sqrt{\mathrm{2}}×\mathrm{6}\sqrt{\mathrm{2}} \\ $$$$=\mathrm{36}\:{sq}.\:{unit} \\ $$$$ \\ $$
Commented by Tawa1 last updated on 24/Nov/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
