Menu Close

Question-48559

Tinku Tara 0 Comments
Pin




Question Number 48559 by behi83417@gmail.com last updated on 25/Nov/18
Answered by tanmay.chaudhury50@gmail.com last updated on 25/Nov/18
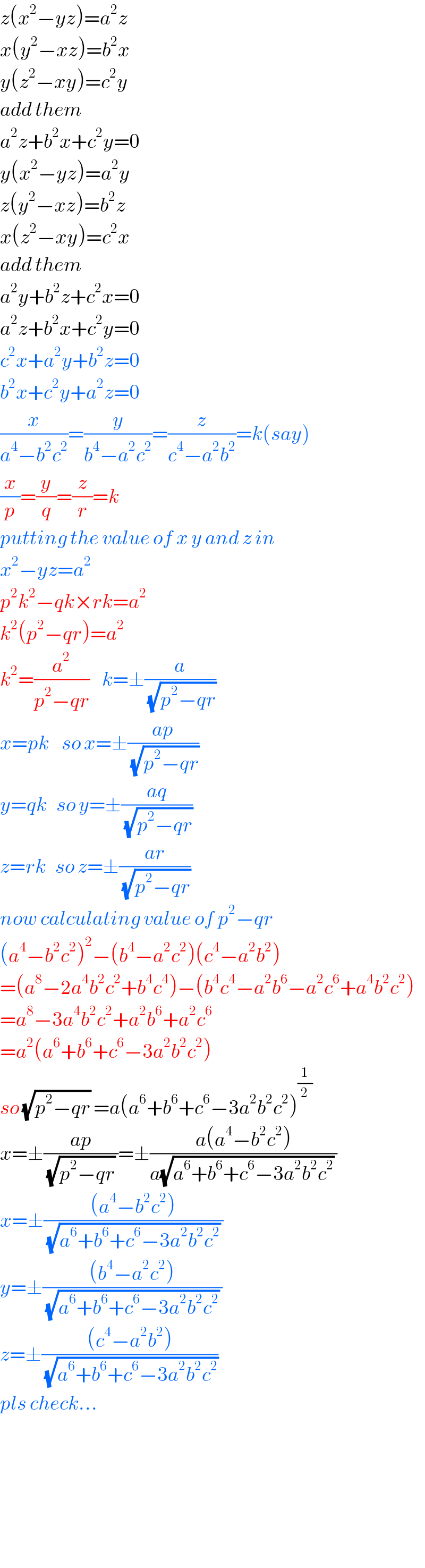
z(x^2 −yz)=a^2 z x(y^2 −xz)=b^2 x y(z^2 −xy)=c^2 y add them a^2 z+b^2 x+c^2 y=0 y(x^2 −yz)=a^2 y z(y^2 −xz)=b^2 z x(z^2 −xy)=c^2 x add them a^2 y+b^2 z+c^2 x=0 a^2 z+b^2 x+c^2 y=0 c^2 x+a^2 y+b^2 z=0 b^2 x+c^2 y+a^2 z=0 (x/(a^4 −b^2 c^2 ))=(y/(b^4 −a^2 c^2 ))=(z/(c^4 −a^2 b^2 ))=k(say) (x/p)=(y/q)=(z/r)=k putting the value of x y and z in x^2 −yz=a^2 p^2 k^2 −qk×rk=a^2 k^2 (p^2 −qr)=a^2 k^2 =(a^2 /(p^2 −qr)) k=±(a/( (√(p^2 −qr)))) x=pk so x=±((ap)/( (√(p^2 −qr)))) y=qk so y=±((aq)/( (√(p^2 −qr)))) z=rk so z=±((ar)/( (√(p^2 −qr)))) now calculating value of p^2 −qr (a^4 −b^2 c^2 )^2 −(b^4 −a^2 c^2 )(c^4 −a^2 b^2 ) =(a^8 −2a^4 b^2 c^2 +b^4 c^4 )−(b^4 c^4 −a^2 b^6 −a^2 c^6 +a^4 b^2 c^2 ) =a^8 −3a^4 b^2 c^2 +a^2 b^6 +a^2 c^6 =a^2 (a^6 +b^6 +c^6 −3a^2 b^2 c^2 ) so (√(p^2 −qr)) =a(a^6 +b^6 +c^6 −3a^2 b^2 c^2 )^(1/2) x=±((ap)/( (√(p^2 −qr)) ))=±((a(a^4 −b^2 c^2 ))/(a(√(a^6 +b^6 +c^6 −3a^2 b^2 c^2 )) )) x=±(((a^4 −b^2 c^2 ))/( (√(a^6 +b^6 +c^6 −3a^2 b^2 c^2 )) )) y=±(((b^4 −a^2 c^2 ))/( (√(a^6 +b^6 +c^6 −3a^2 b^2 c^2 )) )) z=±(((c^4 −a^2 b^2 ))/( (√(a^6 +b^6 +c^6 −3a^2 b^2 c^2 )))) pls check...
$${z}\left({x}^{\mathrm{2}} −{yz}\right)={a}^{\mathrm{2}} {z} \\ $$$${x}\left({y}^{\mathrm{2}} −{xz}\right)={b}^{\mathrm{2}} {x} \\ $$$${y}\left({z}^{\mathrm{2}} −{xy}\right)={c}^{\mathrm{2}} {y} \\ $$$${add}\:{them} \\ $$$${a}^{\mathrm{2}} {z}+{b}^{\mathrm{2}} {x}+{c}^{\mathrm{2}} {y}=\mathrm{0} \\ $$$${y}\left({x}^{\mathrm{2}} −{yz}\right)={a}^{\mathrm{2}} {y} \\ $$$${z}\left({y}^{\mathrm{2}} −{xz}\right)={b}^{\mathrm{2}} {z} \\ $$$${x}\left({z}^{\mathrm{2}} −{xy}\right)={c}^{\mathrm{2}} {x} \\ $$$${add}\:{them}\: \\ $$$${a}^{\mathrm{2}} {y}+{b}^{\mathrm{2}} {z}+{c}^{\mathrm{2}} {x}=\mathrm{0} \\ $$$${a}^{\mathrm{2}} {z}+{b}^{\mathrm{2}} {x}+{c}^{\mathrm{2}} {y}=\mathrm{0} \\ $$$${c}^{\mathrm{2}} {x}+{a}^{\mathrm{2}} {y}+{b}^{\mathrm{2}} {z}=\mathrm{0} \\ $$$${b}^{\mathrm{2}} {x}+{c}^{\mathrm{2}} {y}+{a}^{\mathrm{2}} {z}=\mathrm{0} \\ $$$$\frac{{x}}{{a}^{\mathrm{4}} −{b}^{\mathrm{2}} {c}^{\mathrm{2}} }=\frac{{y}}{{b}^{\mathrm{4}} −{a}^{\mathrm{2}} {c}^{\mathrm{2}} }=\frac{{z}}{{c}^{\mathrm{4}} −{a}^{\mathrm{2}} {b}^{\mathrm{2}} }={k}\left({say}\right) \\ $$$$\frac{{x}}{{p}}=\frac{{y}}{{q}}=\frac{{z}}{{r}}={k} \\ $$$${putting}\:{the}\:{value}\:{of}\:{x}\:{y}\:{and}\:{z}\:{in} \\ $$$${x}^{\mathrm{2}} −{yz}={a}^{\mathrm{2}} \\ $$$${p}^{\mathrm{2}} {k}^{\mathrm{2}} −{qk}×{rk}={a}^{\mathrm{2}} \\ $$$${k}^{\mathrm{2}} \left({p}^{\mathrm{2}} −{qr}\right)={a}^{\mathrm{2}} \\ $$$${k}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} }{{p}^{\mathrm{2}} −{qr}}\:\:\:\:{k}=\pm\frac{{a}}{\:\sqrt{{p}^{\mathrm{2}} −{qr}}} \\ $$$${x}={pk}\:\:\:\:{so}\:{x}=\pm\frac{{ap}}{\:\sqrt{{p}^{\mathrm{2}} −{qr}}} \\ $$$${y}={qk}\:\:\:{so}\:{y}=\pm\frac{{aq}}{\:\sqrt{{p}^{\mathrm{2}} −{qr}}} \\ $$$${z}={rk}\:\:\:{so}\:{z}=\pm\frac{{ar}}{\:\sqrt{{p}^{\mathrm{2}} −{qr}}} \\ $$$${now}\:{calculating}\:{value}\:{of}\:{p}^{\mathrm{2}} −{qr} \\ $$$$\left({a}^{\mathrm{4}} −{b}^{\mathrm{2}} {c}^{\mathrm{2}} \right)^{\mathrm{2}} −\left({b}^{\mathrm{4}} −{a}^{\mathrm{2}} {c}^{\mathrm{2}} \right)\left({c}^{\mathrm{4}} −{a}^{\mathrm{2}} {b}^{\mathrm{2}} \right) \\ $$$$=\left({a}^{\mathrm{8}} −\mathrm{2}{a}^{\mathrm{4}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} +{b}^{\mathrm{4}} {c}^{\mathrm{4}} \right)−\left({b}^{\mathrm{4}} {c}^{\mathrm{4}} −{a}^{\mathrm{2}} {b}^{\mathrm{6}} −{a}^{\mathrm{2}} {c}^{\mathrm{6}} +{a}^{\mathrm{4}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} \right) \\ $$$$={a}^{\mathrm{8}} −\mathrm{3}{a}^{\mathrm{4}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} +{a}^{\mathrm{2}} {b}^{\mathrm{6}} +{a}^{\mathrm{2}} {c}^{\mathrm{6}} \\ $$$$={a}^{\mathrm{2}} \left({a}^{\mathrm{6}} +{b}^{\mathrm{6}} +{c}^{\mathrm{6}} −\mathrm{3}{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} \right) \\ $$$${so}\:\sqrt{{p}^{\mathrm{2}} −{qr}}\:={a}\left({a}^{\mathrm{6}} +{b}^{\mathrm{6}} +{c}^{\mathrm{6}} −\mathrm{3}{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$${x}=\pm\frac{{ap}}{\:\sqrt{{p}^{\mathrm{2}} −{qr}}\:}=\pm\frac{{a}\left({a}^{\mathrm{4}} −{b}^{\mathrm{2}} {c}^{\mathrm{2}} \right)}{{a}\sqrt{{a}^{\mathrm{6}} +{b}^{\mathrm{6}} +{c}^{\mathrm{6}} −\mathrm{3}{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} }\:} \\ $$$${x}=\pm\frac{\left({a}^{\mathrm{4}} −{b}^{\mathrm{2}} {c}^{\mathrm{2}} \right)}{\:\sqrt{{a}^{\mathrm{6}} +{b}^{\mathrm{6}} +{c}^{\mathrm{6}} −\mathrm{3}{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} }\:} \\ $$$${y}=\pm\frac{\left({b}^{\mathrm{4}} −{a}^{\mathrm{2}} {c}^{\mathrm{2}} \right)}{\:\sqrt{{a}^{\mathrm{6}} +{b}^{\mathrm{6}} +{c}^{\mathrm{6}} −\mathrm{3}{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} }\:} \\ $$$${z}=\pm\frac{\left({c}^{\mathrm{4}} −{a}^{\mathrm{2}} {b}^{\mathrm{2}} \right)}{\:\sqrt{{a}^{\mathrm{6}} +{b}^{\mathrm{6}} +{c}^{\mathrm{6}} −\mathrm{3}{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} }} \\ $$$${pls}\:{check}… \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by behi83417@gmail.com last updated on 25/Nov/18
right answer sir.thank you very much.
$${right}\:{answer}\:{sir}.{thank}\:{you}\:{very}\:{much}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 25/Nov/18
thank you sir...
$${thank}\:{you}\:{sir}… \\ $$
Answered by ajfour last updated on 25/Nov/18
(x−y)(x+y+z) = a^2 −b^2 (y−z)(x+y+z) = b^2 −c^2 (z−x)(x+y+z) = c^2 −a^2 ⇒ ((x−y)/(y−z)) = ((a^2 −b^2 )/(b^2 −c^2 )) = p ((y−z)/(z−x)) = ((b^2 −c^2 )/(c^2 −a^2 )) = q ((z−x)/(x−y)) = ((c^2 −a^2 )/(a^2 −b^2 )) = r Now let (x/y) =u , (z/y) = v where u≠1 & v≠ 1 ⇒ u−1= p(1−v) ...(i) & 1−v = q(v−u) ...(ii) & v−u = r(u−1) ...(iii) rewriting (i) & (ii) u+pv = p+1 −qu+(q+1)v = 1 ⇒ v = ((q(p+1)+1)/(pq+q+1)) = 1 ⇒ u = 1 ⇒ u, v not defined ⇒ y = 0 So x^2 = a^2 , z^2 = c^2 , & xz = −b^2 similarly if x= 0, then y^2 = b^2 , z^2 = c^2 , yz = −a^2 And if z=0 x^2 = a^2 , y^2 = b^2 , xy = −c^2 .
$$\left({x}−{y}\right)\left({x}+{y}+{z}\right)\:=\:{a}^{\mathrm{2}} −{b}^{\mathrm{2}} \: \\ $$$$\left({y}−{z}\right)\left({x}+{y}+{z}\right)\:=\:{b}^{\mathrm{2}} −{c}^{\mathrm{2}} \\ $$$$\left({z}−{x}\right)\left({x}+{y}+{z}\right)\:=\:{c}^{\mathrm{2}} −{a}^{\mathrm{2}} \\ $$$$ \\ $$$$\Rightarrow\:\:\:\frac{{x}−{y}}{{y}−{z}}\:=\:\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }\:=\:{p} \\ $$$$\:\:\:\:\:\:\:\:\frac{{y}−{z}}{{z}−{x}}\:=\:\frac{{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }\:=\:{q} \\ $$$$\:\:\:\:\:\:\:\:\frac{{z}−{x}}{{x}−{y}}\:=\:\frac{{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\:=\:{r} \\ $$$${Now}\:\:{let}\:\:\frac{{x}}{{y}}\:={u}\:\:,\:\frac{{z}}{{y}}\:=\:{v} \\ $$$${where}\:\:{u}\neq\mathrm{1}\:\&\:{v}\neq\:\mathrm{1} \\ $$$$\Rightarrow\:\:\:\:{u}−\mathrm{1}=\:{p}\left(\mathrm{1}−{v}\right)\:\:\:\:\:\:\:\:\:\:…\left({i}\right) \\ $$$$\&\:\:\:\:\:\:\mathrm{1}−{v}\:=\:{q}\left({v}−{u}\right)\:\:\:\:\:\:\:\:…\left({ii}\right) \\ $$$$\&\:\:\:\:\:\:{v}−{u}\:=\:{r}\left({u}−\mathrm{1}\right)\:\:\:\:\:\:\:\:…\left({iii}\right) \\ $$$$\:{rewriting}\:\left({i}\right)\:\&\:\left({ii}\right) \\ $$$$\:\:\:\:\:\:\:\:\:{u}+{pv}\:=\:{p}+\mathrm{1} \\ $$$$\:\:\:\:−{qu}+\left({q}+\mathrm{1}\right){v}\:=\:\mathrm{1} \\ $$$$\:\Rightarrow\:\:\:\boldsymbol{{v}}\:=\:\frac{\boldsymbol{{q}}\left(\boldsymbol{{p}}+\mathrm{1}\right)+\mathrm{1}}{\boldsymbol{{pq}}+\boldsymbol{{q}}+\mathrm{1}}\:=\:\mathrm{1}\:\: \\ $$$$\:\Rightarrow\:\:\:\boldsymbol{{u}}\:=\:\mathrm{1} \\ $$$$\:\Rightarrow\:\:{u},\:{v}\:{not}\:{defined} \\ $$$$\Rightarrow\:\:\boldsymbol{{y}}\:=\:\mathrm{0}\: \\ $$$${So}\:\boldsymbol{{x}}^{\mathrm{2}} \:=\:\boldsymbol{{a}}^{\mathrm{2}} ,\:\:\boldsymbol{{z}}^{\mathrm{2}} \:=\:\boldsymbol{{c}}^{\mathrm{2}} \:,\:\&\:\boldsymbol{{xz}}\:=\:−\boldsymbol{{b}}^{\mathrm{2}} \\ $$$${similarly}\:{if}\:\:\boldsymbol{{x}}=\:\mathrm{0},\:{then} \\ $$$$\:\:\:\:\:\:\boldsymbol{{y}}^{\mathrm{2}} \:=\:\boldsymbol{{b}}^{\mathrm{2}} \:,\:\boldsymbol{{z}}^{\mathrm{2}} \:=\:\boldsymbol{{c}}^{\mathrm{2}} \:,\:\boldsymbol{{yz}}\:=\:−\boldsymbol{{a}}^{\mathrm{2}} \\ $$$${And}\:{if}\:\:\boldsymbol{{z}}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\boldsymbol{{x}}^{\mathrm{2}} \:=\:\boldsymbol{{a}}^{\mathrm{2}} ,\:\boldsymbol{{y}}^{\mathrm{2}} \:=\:\boldsymbol{{b}}^{\mathrm{2}} ,\:\boldsymbol{{xy}}\:=\:−\boldsymbol{{c}}^{\mathrm{2}} \:\:. \\ $$
Answered by behi83417@gmail.com last updated on 25/Nov/18
let: r=x+y+z r.(x−y)=a^2 −b^2 (i) r.(y−z)=b^2 −c^2 (ii) r.(z−x)=c^2 −a^2 (iii) 1.if:a^2 =b^2 =c^2 ⇒ { (([x=y=z⇒a=b=c=0])),(([r=x+y+z=0⇒x^2 +xy+y^2 =a^2 ]∗)) :} from(∗)we can take any valve for x and then obtain other varibles. 2.if: a^2 ,or b^2 ,or c^2 ,or a^2 +b^2 +c^2 ≠0,we have: r.y=r.x−(a^2 −b^2 ) r.z=r.x+(c^2 −a^2 ) ⇒r^2 =r.(x+y+z)=3r.x+(b^2 +c^2 −2a^2 ) or: 3r.x=r^2 +(2a^2 −b^2 −c^2 ) (X) 3r.y=r^2 +(2b^2 −a^2 −c^2 ) (Y) 3r.z=r^2 +(2c^2 −a^2 −b^2 ) (Z) also we have: (x−y)^2 +(y−x)^2 +(z−x)^2 =2(a^2 +b^2 +c^2 ) now from (i,ii,iii)and this↑have: r^2 =(((a^2 −b^2 )^2 +(b^2 −c^2 )^2 +(c^2 −a^2 )^2 )/(2(a^2 +b^2 +c^2 )))=^(after symplifing) =((a^6 +b^6 +c^6 −3a^2 b^2 c^2 )/((a^2 +b^2 +c^2 )^2 )) now from: (X)⇒ x=(1/(3r))[r^2 +(2a^2 −b^2 −c^2 )]=^(after symplifing) =((a^4 −b^2 c^2 )/( (√(a^6 +b^6 +c^6 −3a^2 b^2 c^2 )))). and finally: x=((a^4 −b^2 c^2 )/( (√(a^6 +b^6 +c^6 −3a^2 b^2 c^2 )))) y=((b^4 −a^2 c^2 )/( (√(a^6 +b^6 +c^6 −3a^2 b^2 c^2 )))) z=((c^4 −a^2 b^2 )/( (√(a^6 +b^6 +c^6 −3a^2 b^2 c^2 )))) .
$${let}:\:{r}={x}+{y}+{z} \\ $$$${r}.\left({x}−{y}\right)={a}^{\mathrm{2}} −{b}^{\mathrm{2}} \:\left({i}\right) \\ $$$${r}.\left({y}−{z}\right)={b}^{\mathrm{2}} −{c}^{\mathrm{2}} \:\left({ii}\right) \\ $$$${r}.\left({z}−{x}\right)={c}^{\mathrm{2}} −{a}^{\mathrm{2}} \:\left({iii}\right) \\ $$$$\mathrm{1}.{if}:{a}^{\mathrm{2}} ={b}^{\mathrm{2}} ={c}^{\mathrm{2}} \Rightarrow\begin{cases}{\left[{x}={y}={z}\Rightarrow{a}={b}={c}=\mathrm{0}\right]}\\{\left[{r}={x}+{y}+{z}=\mathrm{0}\Rightarrow{x}^{\mathrm{2}} +{xy}+{y}^{\mathrm{2}} ={a}^{\mathrm{2}} \right]\ast}\end{cases} \\ $$$${from}\left(\ast\right){we}\:{can}\:{take}\:{any}\:{valve}\:{for}\:{x} \\ $$$${and}\:{then}\:{obtain}\:{other}\:{varibles}. \\ $$$$\mathrm{2}.{if}:\:{a}^{\mathrm{2}} ,{or}\:{b}^{\mathrm{2}} ,{or}\:{c}^{\mathrm{2}} ,{or}\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \neq\mathrm{0},{we}\:{have}: \\ $$$${r}.{y}={r}.{x}−\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right) \\ $$$${r}.{z}={r}.{x}+\left({c}^{\mathrm{2}} −{a}^{\mathrm{2}} \right) \\ $$$$\Rightarrow{r}^{\mathrm{2}} ={r}.\left({x}+{y}+{z}\right)=\mathrm{3}{r}.{x}+\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{a}^{\mathrm{2}} \right) \\ $$$${or}:\:\mathrm{3}{r}.{x}={r}^{\mathrm{2}} +\left(\mathrm{2}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)\:\left(\boldsymbol{\mathrm{X}}\right) \\ $$$$\:\:\:\:\:\:\:\mathrm{3}{r}.{y}={r}^{\mathrm{2}} +\left(\mathrm{2}{b}^{\mathrm{2}} −{a}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)\:\left(\boldsymbol{\mathrm{Y}}\right) \\ $$$$\:\:\:\:\:\:\:\mathrm{3}{r}.{z}={r}^{\mathrm{2}} +\left(\mathrm{2}{c}^{\mathrm{2}} −{a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\:\left(\boldsymbol{\mathrm{Z}}\right) \\ $$$${also}\:{we}\:{have}: \\ $$$$\left({x}−{y}\right)^{\mathrm{2}} +\left({y}−{x}\right)^{\mathrm{2}} +\left({z}−{x}\right)^{\mathrm{2}} =\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\: \\ $$$${now}\:{from}\:\left({i},{ii},{iii}\right){and}\:{this}\uparrow{have}: \\ $$$$\boldsymbol{{r}}^{\mathrm{2}} =\frac{\left(\boldsymbol{{a}}^{\mathrm{2}} −\boldsymbol{{b}}^{\mathrm{2}} \right)^{\mathrm{2}} +\left(\boldsymbol{{b}}^{\mathrm{2}} −\boldsymbol{{c}}^{\mathrm{2}} \right)^{\mathrm{2}} +\left(\boldsymbol{{c}}^{\mathrm{2}} −\boldsymbol{{a}}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{2}\left(\boldsymbol{{a}}^{\mathrm{2}} +\boldsymbol{{b}}^{\mathrm{2}} +\boldsymbol{{c}}^{\mathrm{2}} \right)}\overset{{after}\:{symplifing}} {=} \\ $$$$=\frac{\boldsymbol{{a}}^{\mathrm{6}} +\boldsymbol{{b}}^{\mathrm{6}} +\boldsymbol{{c}}^{\mathrm{6}} −\mathrm{3}\boldsymbol{{a}}^{\mathrm{2}} \boldsymbol{{b}}^{\mathrm{2}} \boldsymbol{{c}}^{\mathrm{2}} }{\left(\boldsymbol{{a}}^{\mathrm{2}} +\boldsymbol{{b}}^{\mathrm{2}} +\boldsymbol{{c}}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$${now}\:{from}:\:\left(\boldsymbol{\mathrm{X}}\right)\Rightarrow \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{3}{r}}\left[{r}^{\mathrm{2}} +\left(\mathrm{2}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)\right]\overset{{after}\:{symplifing}} {=} \\ $$$$=\frac{\boldsymbol{{a}}^{\mathrm{4}} −\boldsymbol{{b}}^{\mathrm{2}} \boldsymbol{{c}}^{\mathrm{2}} }{\:\sqrt{\boldsymbol{{a}}^{\mathrm{6}} +\boldsymbol{{b}}^{\mathrm{6}} +\boldsymbol{{c}}^{\mathrm{6}} −\mathrm{3}\boldsymbol{{a}}^{\mathrm{2}} \boldsymbol{{b}}^{\mathrm{2}} \boldsymbol{{c}}^{\mathrm{2}} }}. \\ $$$$\boldsymbol{{and}}\:\boldsymbol{{finally}}: \\ $$$$\boldsymbol{\mathrm{x}}=\frac{\boldsymbol{\mathrm{a}}^{\mathrm{4}} −\boldsymbol{\mathrm{b}}^{\mathrm{2}} \boldsymbol{\mathrm{c}}^{\mathrm{2}} }{\:\sqrt{\boldsymbol{\mathrm{a}}^{\mathrm{6}} +\boldsymbol{\mathrm{b}}^{\mathrm{6}} +\boldsymbol{\mathrm{c}}^{\mathrm{6}} −\mathrm{3}\boldsymbol{\mathrm{a}}^{\mathrm{2}} \boldsymbol{\mathrm{b}}^{\mathrm{2}} \boldsymbol{\mathrm{c}}^{\mathrm{2}} }} \\ $$$$\boldsymbol{\mathrm{y}}=\frac{\boldsymbol{\mathrm{b}}^{\mathrm{4}} −\boldsymbol{\mathrm{a}}^{\mathrm{2}} \boldsymbol{\mathrm{c}}^{\mathrm{2}} }{\:\sqrt{\boldsymbol{\mathrm{a}}^{\mathrm{6}} +\boldsymbol{\mathrm{b}}^{\mathrm{6}} +\boldsymbol{\mathrm{c}}^{\mathrm{6}} −\mathrm{3}\boldsymbol{\mathrm{a}}^{\mathrm{2}} \boldsymbol{\mathrm{b}}^{\mathrm{2}} \boldsymbol{\mathrm{c}}^{\mathrm{2}} }} \\ $$$$\boldsymbol{\mathrm{z}}=\frac{\boldsymbol{\mathrm{c}}^{\mathrm{4}} −\boldsymbol{\mathrm{a}}^{\mathrm{2}} \boldsymbol{\mathrm{b}}^{\mathrm{2}} }{\:\sqrt{\boldsymbol{\mathrm{a}}^{\mathrm{6}} +\boldsymbol{\mathrm{b}}^{\mathrm{6}} +\boldsymbol{\mathrm{c}}^{\mathrm{6}} −\mathrm{3}\boldsymbol{\mathrm{a}}^{\mathrm{2}} \boldsymbol{\mathrm{b}}^{\mathrm{2}} \boldsymbol{\mathrm{c}}^{\mathrm{2}} }}\:\:\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *