Menu Close

Question-48611

Tinku Tara 0 Comments
Pin




Question Number 48611 by Tawa1 last updated on 25/Nov/18
Answered by mr W last updated on 26/Nov/18
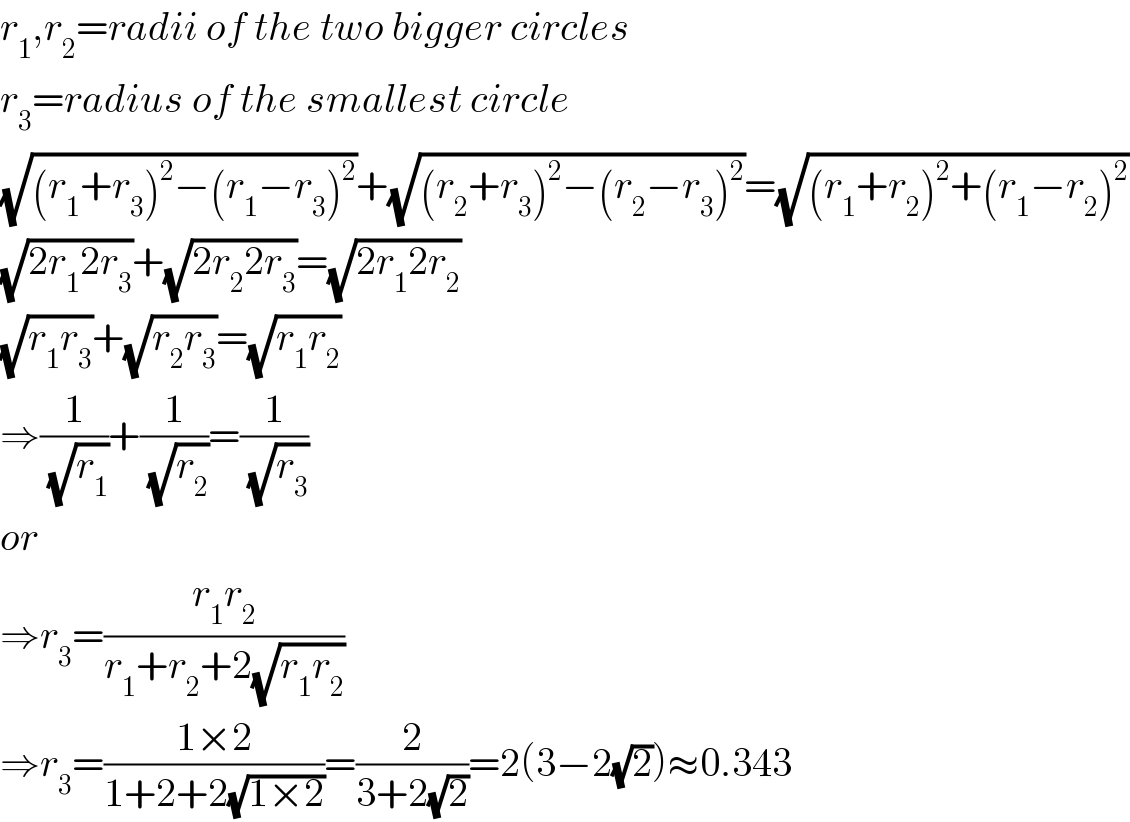
r_1 ,r_2 =radii of the two bigger circles r_3 =radius of the smallest circle (√((r_1 +r_3 )^2 −(r_1 −r_3 )^2 ))+(√((r_2 +r_3 )^2 −(r_2 −r_3 )^2 ))=(√((r_1 +r_2 )^2 +(r_1 −r_2 )^2 )) (√(2r_1 2r_3 ))+(√(2r_2 2r_3 ))=(√(2r_1 2r_2 )) (√(r_1 r_3 ))+(√(r_2 r_3 ))=(√(r_1 r_2 )) ⇒(1/( (√r_1 )))+(1/( (√r_2 )))=(1/( (√r_3 ))) or ⇒r_3 =((r_1 r_2 )/(r_1 +r_2 +2(√(r_1 r_2 )))) ⇒r_3 =((1×2)/(1+2+2(√(1×2))))=(2/(3+2(√2)))=2(3−2(√2))≈0.343
$${r}_{\mathrm{1}} ,{r}_{\mathrm{2}} ={radii}\:{of}\:{the}\:{two}\:{bigger}\:{circles} \\ $$$${r}_{\mathrm{3}} ={radius}\:{of}\:{the}\:{smallest}\:{circle} \\ $$$$\sqrt{\left({r}_{\mathrm{1}} +{r}_{\mathrm{3}} \right)^{\mathrm{2}} −\left({r}_{\mathrm{1}} −{r}_{\mathrm{3}} \right)^{\mathrm{2}} }+\sqrt{\left({r}_{\mathrm{2}} +{r}_{\mathrm{3}} \right)^{\mathrm{2}} −\left({r}_{\mathrm{2}} −{r}_{\mathrm{3}} \right)^{\mathrm{2}} }=\sqrt{\left({r}_{\mathrm{1}} +{r}_{\mathrm{2}} \right)^{\mathrm{2}} +\left({r}_{\mathrm{1}} −{r}_{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\sqrt{\mathrm{2}{r}_{\mathrm{1}} \mathrm{2}{r}_{\mathrm{3}} }+\sqrt{\mathrm{2}{r}_{\mathrm{2}} \mathrm{2}{r}_{\mathrm{3}} }=\sqrt{\mathrm{2}{r}_{\mathrm{1}} \mathrm{2}{r}_{\mathrm{2}} } \\ $$$$\sqrt{{r}_{\mathrm{1}} {r}_{\mathrm{3}} }+\sqrt{{r}_{\mathrm{2}} {r}_{\mathrm{3}} }=\sqrt{{r}_{\mathrm{1}} {r}_{\mathrm{2}} } \\ $$$$\Rightarrow\frac{\mathrm{1}}{\:\sqrt{{r}_{\mathrm{1}} }}+\frac{\mathrm{1}}{\:\sqrt{{r}_{\mathrm{2}} }}=\frac{\mathrm{1}}{\:\sqrt{{r}_{\mathrm{3}} }} \\ $$$${or} \\ $$$$\Rightarrow{r}_{\mathrm{3}} =\frac{{r}_{\mathrm{1}} {r}_{\mathrm{2}} }{{r}_{\mathrm{1}} +{r}_{\mathrm{2}} +\mathrm{2}\sqrt{{r}_{\mathrm{1}} {r}_{\mathrm{2}} }} \\ $$$$\Rightarrow{r}_{\mathrm{3}} =\frac{\mathrm{1}×\mathrm{2}}{\mathrm{1}+\mathrm{2}+\mathrm{2}\sqrt{\mathrm{1}×\mathrm{2}}}=\frac{\mathrm{2}}{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}}=\mathrm{2}\left(\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\right)\approx\mathrm{0}.\mathrm{343} \\ $$
Commented by Tawa1 last updated on 26/Nov/18
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by Tawa1 last updated on 26/Nov/18
Sir, does this work for every circle like this ?
$$\mathrm{Sir},\:\mathrm{does}\:\mathrm{this}\:\mathrm{work}\:\mathrm{for}\:\mathrm{every}\:\mathrm{circle}\:\mathrm{like}\:\mathrm{this}\:?\: \\ $$
Commented by Tawa1 last updated on 26/Nov/18
And please sir, reference prove of similar circle you have prove here before. I want to understand the concept of the question God bless you sir
$$\mathrm{And}\:\mathrm{please}\:\mathrm{sir},\:\mathrm{reference}\:\mathrm{prove}\:\mathrm{of}\:\mathrm{similar}\:\mathrm{circle}\:\mathrm{you}\:\mathrm{have}\:\mathrm{prove} \\ $$$$\mathrm{here}\:\mathrm{before}.\:\:\mathrm{I}\:\mathrm{want}\:\mathrm{to}\:\mathrm{understand}\:\mathrm{the}\:\mathrm{concept}\:\mathrm{of}\:\mathrm{the}\:\mathrm{question} \\ $$$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by mr W last updated on 26/Nov/18
Commented by mr W last updated on 26/Nov/18
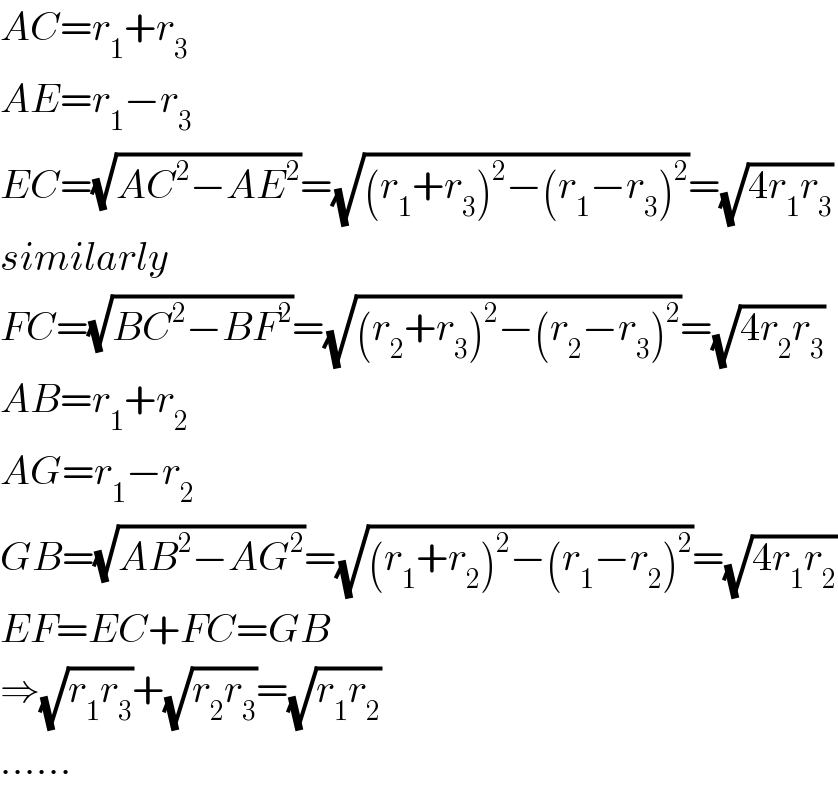
AC=r_1 +r_3 AE=r_1 −r_3 EC=(√(AC^2 −AE^2 ))=(√((r_1 +r_3 )^2 −(r_1 −r_3 )^2 ))=(√(4r_1 r_3 )) similarly FC=(√(BC^2 −BF^2 ))=(√((r_2 +r_3 )^2 −(r_2 −r_3 )^2 ))=(√(4r_2 r_3 )) AB=r_1 +r_2 AG=r_1 −r_2 GB=(√(AB^2 −AG^2 ))=(√((r_1 +r_2 )^2 −(r_1 −r_2 )^2 ))=(√(4r_1 r_2 )) EF=EC+FC=GB ⇒(√(r_1 r_3 ))+(√(r_2 r_3 ))=(√(r_1 r_2 )) ......
$${AC}={r}_{\mathrm{1}} +{r}_{\mathrm{3}} \\ $$$${AE}={r}_{\mathrm{1}} −{r}_{\mathrm{3}} \\ $$$${EC}=\sqrt{{AC}^{\mathrm{2}} −{AE}^{\mathrm{2}} }=\sqrt{\left({r}_{\mathrm{1}} +{r}_{\mathrm{3}} \right)^{\mathrm{2}} −\left({r}_{\mathrm{1}} −{r}_{\mathrm{3}} \right)^{\mathrm{2}} }=\sqrt{\mathrm{4}{r}_{\mathrm{1}} {r}_{\mathrm{3}} } \\ $$$${similarly} \\ $$$${FC}=\sqrt{{BC}^{\mathrm{2}} −{BF}^{\mathrm{2}} }=\sqrt{\left({r}_{\mathrm{2}} +{r}_{\mathrm{3}} \right)^{\mathrm{2}} −\left({r}_{\mathrm{2}} −{r}_{\mathrm{3}} \right)^{\mathrm{2}} }=\sqrt{\mathrm{4}{r}_{\mathrm{2}} {r}_{\mathrm{3}} } \\ $$$${AB}={r}_{\mathrm{1}} +{r}_{\mathrm{2}} \\ $$$${AG}={r}_{\mathrm{1}} −{r}_{\mathrm{2}} \\ $$$${GB}=\sqrt{{AB}^{\mathrm{2}} −{AG}^{\mathrm{2}} }=\sqrt{\left({r}_{\mathrm{1}} +{r}_{\mathrm{2}} \right)^{\mathrm{2}} −\left({r}_{\mathrm{1}} −{r}_{\mathrm{2}} \right)^{\mathrm{2}} }=\sqrt{\mathrm{4}{r}_{\mathrm{1}} {r}_{\mathrm{2}} } \\ $$$${EF}={EC}+{FC}={GB} \\ $$$$\Rightarrow\sqrt{{r}_{\mathrm{1}} {r}_{\mathrm{3}} }+\sqrt{{r}_{\mathrm{2}} {r}_{\mathrm{3}} }=\sqrt{{r}_{\mathrm{1}} {r}_{\mathrm{2}} } \\ $$$$…… \\ $$
Commented by Tawa1 last updated on 26/Nov/18
God bless you sir. I appreciate your time
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *