Question Number 48757 by sandeepkeshari0797@gmail.com last updated on 28/Nov/18
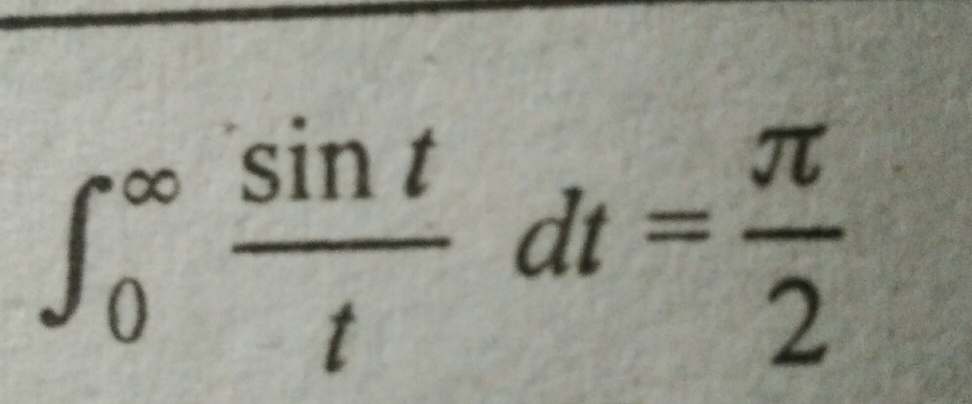
Commented by maxmathsup by imad last updated on 28/Nov/18
![method with one parametr let f(x)=∫_0 ^∞ ((sint)/t) e^(−tx) dt with x≥0 we have f^′ (x)=−∫_0 ^∞ sint e^(−tx) dt =−Im(∫_0 ^∞ e^(it−xt) dt) but ∫_0 ^∞ e^((−x+i)t) dt =[(1/(−x+i)) e^((−x+i)t) ]_(t=0) ^∞ =−(1/(−x+i)) =(1/(x−i)) =((x+i)/(x^2 +1)) ⇒ f^′ (x)=−(1/(1+x^2 )) ⇒ f(x)=−arctan(x)+c we have c=lim_(x→+∞) (f(x)+arctan(x)) =(π/2) +lim_(x→+∞) f(x) but ∃m>0 / ∣f(x)∣≤∫_0 ^∞ ∣((sint)/t)∣e^(−tx) dt ≤m ∫_0 ^∞ e^(−tx) dt =(m/x) →0 (x→+∞) ⇒c=(π/2) so ∫_0 ^∞ ((sin(t))/t) e^(−xt) dt =(π/2) −arctan(x) x=0 ⇒∫_0 ^∞ ((sint)/t) dt =(π/2) .](https://www.tinkutara.com/question/Q48800.png)
$${method}\:{with}\:{one}\:{parametr}\:{let}\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{sint}}{{t}}\:{e}^{−{tx}} {dt}\:{with}\:{x}\geqslant\mathrm{0}\:{we}\:{have} \\ $$$${f}^{'} \left({x}\right)=−\int_{\mathrm{0}} ^{\infty} \:\:{sint}\:{e}^{−{tx}} {dt}\:=−{Im}\left(\int_{\mathrm{0}} ^{\infty} \:{e}^{{it}−{xt}} {dt}\right)\:{but} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:{e}^{\left(−{x}+{i}\right){t}} {dt}\:=\left[\frac{\mathrm{1}}{−{x}+{i}}\:{e}^{\left(−{x}+{i}\right){t}} \right]_{{t}=\mathrm{0}} ^{\infty} \:=−\frac{\mathrm{1}}{−{x}+{i}}\:=\frac{\mathrm{1}}{{x}−{i}}\:=\frac{{x}+{i}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$${f}^{'} \left({x}\right)=−\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\:\Rightarrow\:{f}\left({x}\right)=−{arctan}\left({x}\right)+{c}\:{we}\:{have} \\ $$$${c}={lim}_{{x}\rightarrow+\infty} \left({f}\left({x}\right)+{arctan}\left({x}\right)\right)\:=\frac{\pi}{\mathrm{2}}\:+{lim}_{{x}\rightarrow+\infty} {f}\left({x}\right)\:{but}\:\exists{m}>\mathrm{0}\:/ \\ $$$$\mid{f}\left({x}\right)\mid\leqslant\int_{\mathrm{0}} ^{\infty} \:\mid\frac{{sint}}{{t}}\mid{e}^{−{tx}} {dt}\:\leqslant{m}\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{tx}} {dt}\:=\frac{{m}}{{x}}\:\rightarrow\mathrm{0}\:\left({x}\rightarrow+\infty\right)\:\Rightarrow{c}=\frac{\pi}{\mathrm{2}}\:{so} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{sin}\left({t}\right)}{{t}}\:{e}^{−{xt}} {dt}\:=\frac{\pi}{\mathrm{2}}\:−{arctan}\left({x}\right)\: \\ $$$${x}=\mathrm{0}\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\:\frac{{sint}}{{t}}\:{dt}\:=\frac{\pi}{\mathrm{2}}\:. \\ $$
Commented by maxmathsup by imad last updated on 01/Dec/18

$${f}\left({x}\right)={L}\left(\frac{{sinx}}{{x}}\right). \\ $$
Answered by Abdulhafeez Abu qatada last updated on 28/Nov/18
![using Laplace transforms L{((f(t))/t)} = ∫_(σ=s) ^∞ F(σ) dσ L{sint} = F(s) = (1/(s^2 + 1)),F(σ) = (1/(σ^2 + 1)) L{((sint)/t)} = ∫_(σ=s) ^∞ (1/(σ^2 + 1)) dσ L{((sint)/t)} = [tan^(−1) {σ}]_(σ=s) ^∞ L{((sint)/t)} = (π/2) − tan^(−1) {s} L{((sint)/t)} = tan^(−1) {(1/s)} L{((sint)/t)} = ∫_0 ^∞ ((sint)/t).e^(−st) = tan^(−1) {(1/s)} when s = 0 ∫_0 ^∞ ((sint)/t).e^(−(0)t) = lim_(s→0) (tan^(−1) {(1/s)}) = (π/2) ∫_0 ^∞ ((sint)/t) = (π/2)](https://www.tinkutara.com/question/Q48758.png)
$$ \\ $$$$ \\ $$$${using}\:{Laplace}\:{transforms} \\ $$$${L}\left\{\frac{{f}\left({t}\right)}{{t}}\right\}\:=\:\underset{\sigma={s}} {\overset{\infty} {\int}}{F}\left(\sigma\right)\:{d}\sigma\: \\ $$$${L}\left\{{sint}\right\}\:=\:{F}\left({s}\right)\:=\:\frac{\mathrm{1}}{{s}^{\mathrm{2}} \:+\:\mathrm{1}},{F}\left(\sigma\right)\:=\:\frac{\mathrm{1}}{\sigma^{\mathrm{2}} \:+\:\mathrm{1}} \\ $$$$ \\ $$$${L}\left\{\frac{{sint}}{{t}}\right\}\:=\:\underset{\sigma={s}} {\overset{\infty} {\int}}\:\frac{\mathrm{1}}{\sigma^{\mathrm{2}} \:+\:\mathrm{1}}\:{d}\sigma\: \\ $$$${L}\left\{\frac{{sint}}{{t}}\right\}\:=\:\left[{tan}^{−\mathrm{1}} \left\{\sigma\right\}\right]_{\sigma={s}} ^{\infty} \\ $$$${L}\left\{\frac{{sint}}{{t}}\right\}\:=\:\frac{\pi}{\mathrm{2}}\:−\:{tan}^{−\mathrm{1}} \left\{{s}\right\} \\ $$$${L}\left\{\frac{{sint}}{{t}}\right\}\:=\:{tan}^{−\mathrm{1}} \left\{\frac{\mathrm{1}}{{s}}\right\} \\ $$$${L}\left\{\frac{{sint}}{{t}}\right\}\:=\:\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{sint}}{{t}}.{e}^{−{st}} \:=\:{tan}^{−\mathrm{1}} \left\{\frac{\mathrm{1}}{{s}}\right\} \\ $$$${when}\:{s}\:=\:\mathrm{0} \\ $$$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{sint}}{{t}}.{e}^{−\left(\mathrm{0}\right){t}} \:=\:\underset{{s}\rightarrow\mathrm{0}} {\mathrm{lim}}\left({tan}^{−\mathrm{1}} \left\{\frac{\mathrm{1}}{{s}}\right\}\right)\:=\:\frac{\pi}{\mathrm{2}} \\ $$$$ \\ $$$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{sint}}{{t}}\:=\:\frac{\pi}{\mathrm{2}} \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 28/Nov/18
![solving another way...let I=∫_0 ^∞ ((e^(−at) sinbt)/t)dt (dI/db)=∫_0 ^∞ (e^(−at) /t)×(∂/∂b)(sinbt)dt (dI/db)=∫_0 ^∞ ((e^(−at) cosbt×t)/t)dt (dI/db)=∫_0 ^∞ e^(−at) cosbtdt=(a^ /(a^2 +b^2 ))[forula] ∫_0 ^∞ e^(−at) sinbt dt=(b/(a^2 +b^2 )) [formula] now (dI/db)=(a/(a^2 +b^2 )) dI=((adb)/(a^2 +b^2 )) ∫dI=a∫(db/(a^2 +b^2 )) I=a×(1/a)tan^(−1) ((b/a))+c put b=0 in ∫_0 ^∞ ((e^(−at) sinbt)/t)dt results=0 so 0=tan^(−1) ((0/a))+c hence c=0 I=tan^(−1) ((b/a)) so ∫_0 ^∞ ((e^(−at) sinbt)/t)=tan^(−1) ((b/a)) but question is ∫_0 ^∞ ((sint)/t)dt so put a=0 b=1 in tan^(−1) ((b/a)) =tan^(−1) ((1/0))=(π/2) answer](https://www.tinkutara.com/question/Q48778.png)
$${solving}\:{another}\:{way}…{let} \\ $$$${I}=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{at}} {sinbt}}{{t}}{dt} \\ $$$$\frac{{dI}}{{db}}=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{at}} }{{t}}×\frac{\partial}{\partial{b}}\left({sinbt}\right){dt} \\ $$$$\frac{{dI}}{{db}}=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{at}} {cosbt}×{t}}{{t}}{dt} \\ $$$$\frac{{dI}}{{db}}=\int_{\mathrm{0}} ^{\infty} {e}^{−{at}} {cosbtdt}=\frac{{a}^{} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\left[{forula}\right] \\ $$$$\int_{\mathrm{0}} ^{\infty} {e}^{−{at}} {sinbt}\:{dt}=\frac{{b}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:\left[{formula}\right] \\ $$$${now}\:\frac{{dI}}{{db}}=\frac{{a}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$${dI}=\frac{{adb}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$\int{dI}={a}\int\frac{{db}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$${I}={a}×\frac{\mathrm{1}}{{a}}{tan}^{−\mathrm{1}} \left(\frac{{b}}{{a}}\right)+{c} \\ $$$${put}\:{b}=\mathrm{0}\:{in}\:\:\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{at}} {sinbt}}{{t}}{dt}\:\:{results}=\mathrm{0} \\ $$$${so}\:\mathrm{0}={tan}^{−\mathrm{1}} \left(\frac{\mathrm{0}}{{a}}\right)+{c}\:\:{hence}\:{c}=\mathrm{0} \\ $$$${I}={tan}^{−\mathrm{1}} \left(\frac{{b}}{{a}}\right) \\ $$$${so}\:\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{at}} {sinbt}}{{t}}={tan}^{−\mathrm{1}} \left(\frac{{b}}{{a}}\right) \\ $$$${but}\:{question}\:{is}\:\int_{\mathrm{0}} ^{\infty} \frac{{sint}}{{t}}{dt} \\ $$$${so}\:{put}\:{a}=\mathrm{0}\:\:\:{b}=\mathrm{1}\:{in}\:{tan}^{−\mathrm{1}} \left(\frac{{b}}{{a}}\right) \\ $$$$={tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{0}}\right)=\frac{\pi}{\mathrm{2}}\:\:{answer} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by Abdulhafeez Abu qatada last updated on 28/Nov/18

$${wonderful}… \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 28/Nov/18

$${thank}\:{you}\:{sir}… \\ $$
