Menu Close

Question-48871

Tinku Tara 0 Comments
Pin




Question Number 48871 by peter frank last updated on 29/Nov/18
Commented by maxmathsup by imad last updated on 01/Jan/19
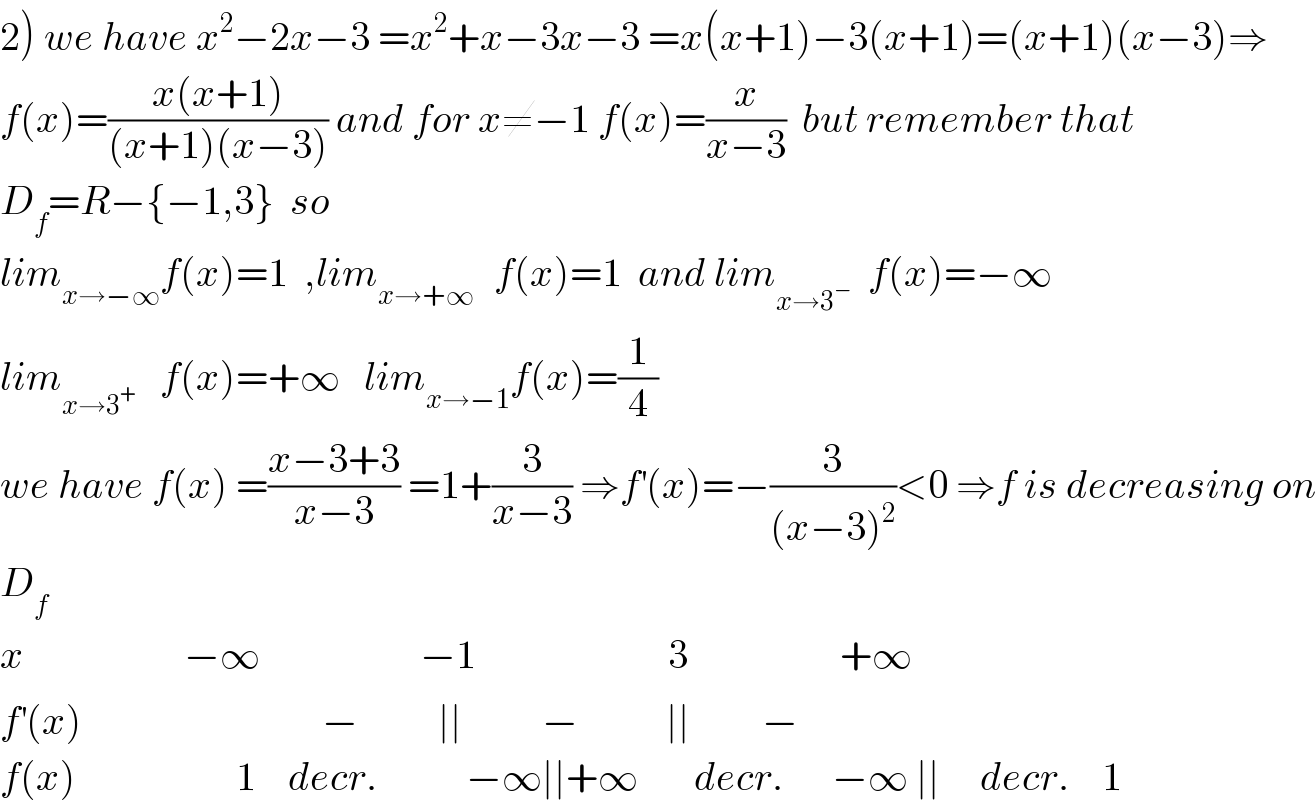
2) we have x^2 −2x−3 =x^2 +x−3x−3 =x(x+1)−3(x+1)=(x+1)(x−3)⇒ f(x)=((x(x+1))/((x+1)(x−3))) and for x≠−1 f(x)=(x/(x−3)) but remember that D_f =R−{−1,3} so lim_(x→−∞) f(x)=1 ,lim_(x→+∞ ) f(x)=1 and lim_(x→3^− ) f(x)=−∞ lim_(x→3^+ ) f(x)=+∞ lim_(x→−1) f(x)=(1/4) we have f(x) =((x−3+3)/(x−3)) =1+(3/(x−3)) ⇒f^′ (x)=−(3/((x−3)^2 ))<0 ⇒f is decreasing on D_f x −∞ −1 3 +∞ f^′ (x) − ∣∣ − ∣∣ − f(x) 1 decr. −∞∣∣+∞ decr. −∞ ∣∣ decr. 1
$$\left.\mathrm{2}\right)\:{we}\:{have}\:{x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{3}\:={x}^{\mathrm{2}} +{x}−\mathrm{3}{x}−\mathrm{3}\:={x}\left({x}+\mathrm{1}\right)−\mathrm{3}\left({x}+\mathrm{1}\right)=\left({x}+\mathrm{1}\right)\left({x}−\mathrm{3}\right)\Rightarrow \\ $$$${f}\left({x}\right)=\frac{{x}\left({x}+\mathrm{1}\right)}{\left({x}+\mathrm{1}\right)\left({x}−\mathrm{3}\right)}\:{and}\:{for}\:{x}\neq−\mathrm{1}\:{f}\left({x}\right)=\frac{{x}}{{x}−\mathrm{3}}\:\:{but}\:{remember}\:{that} \\ $$$${D}_{{f}} ={R}−\left\{−\mathrm{1},\mathrm{3}\right\}\:\:{so} \\ $$$${lim}_{{x}\rightarrow−\infty} {f}\left({x}\right)=\mathrm{1}\:\:,{lim}_{{x}\rightarrow+\infty\:} \:\:{f}\left({x}\right)=\mathrm{1}\:\:{and}\:{lim}_{{x}\rightarrow\mathrm{3}^{−} } \:\:{f}\left({x}\right)=−\infty\: \\ $$$${lim}_{{x}\rightarrow\mathrm{3}^{+} } \:\:\:{f}\left({x}\right)=+\infty\:\:\:{lim}_{{x}\rightarrow−\mathrm{1}} {f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${we}\:{have}\:{f}\left({x}\right)\:=\frac{{x}−\mathrm{3}+\mathrm{3}}{{x}−\mathrm{3}}\:=\mathrm{1}+\frac{\mathrm{3}}{{x}−\mathrm{3}}\:\Rightarrow{f}^{'} \left({x}\right)=−\frac{\mathrm{3}}{\left({x}−\mathrm{3}\right)^{\mathrm{2}} }<\mathrm{0}\:\Rightarrow{f}\:{is}\:{decreasing}\:{on} \\ $$$${D}_{{f}} \\ $$$${x}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\infty\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\infty \\ $$$${f}^{'} \left({x}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\:\:\:\:\:\:\:\:\:\:\mid\mid\:\:\:\:\:\:\:\:\:\:−\:\:\:\:\:\:\:\:\:\:\:\mid\mid\:\:\:\:\:\:\:\:\:− \\ $$$${f}\left({x}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:{decr}.\:\:\:\:\:\:\:\:\:\:\:−\infty\mid\mid+\infty\:\:\:\:\:\:\:{decr}.\:\:\:\:\:\:−\infty\:\mid\mid\:\:\:\:\:{decr}.\:\:\:\:\mathrm{1} \\ $$
Answered by kaivan.ahmadi last updated on 30/Nov/18
lim_(x→∞) f(x)=1⇒y=1 is horizontal asympote x^2 −2x−3=0⇒(x−3)(x+1)=0⇒ x=3 x=−1 but since x=−1 is root of x^2 +x=0 is not vertical asympote so x=3 is vertical asympote
$$\mathrm{lim}_{\mathrm{x}\rightarrow\infty} \mathrm{f}\left(\mathrm{x}\right)=\mathrm{1}\Rightarrow\mathrm{y}=\mathrm{1}\:\mathrm{is}\:\mathrm{horizontal} \\ $$$$\mathrm{asympote} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{2x}−\mathrm{3}=\mathrm{0}\Rightarrow\left(\mathrm{x}−\mathrm{3}\right)\left(\mathrm{x}+\mathrm{1}\right)=\mathrm{0}\Rightarrow \\ $$$$\mathrm{x}=\mathrm{3} \\ $$$$\mathrm{x}=−\mathrm{1} \\ $$$$\mathrm{but}\:\mathrm{since}\:\mathrm{x}=−\mathrm{1}\:\mathrm{is}\:\mathrm{root}\:\mathrm{of}\:\mathrm{x}^{\mathrm{2}} +\mathrm{x}=\mathrm{0} \\ $$$$\mathrm{is}\:\mathrm{not}\:\mathrm{vertical}\:\mathrm{asympote} \\ $$$$\mathrm{so}\:\mathrm{x}=\mathrm{3}\:\mathrm{is}\:\mathrm{vertical}\:\mathrm{asympote} \\ $$
Answered by kaivan.ahmadi last updated on 30/Nov/18
D_f =R−{−1,3} R_f =R−{1}
$$\mathrm{D}_{\mathrm{f}} =\mathrm{R}−\left\{−\mathrm{1},\mathrm{3}\right\} \\ $$$$\mathrm{R}_{\mathrm{f}} =\mathrm{R}−\left\{\mathrm{1}\right\} \\ $$
Answered by kaivan.ahmadi last updated on 30/Nov/18
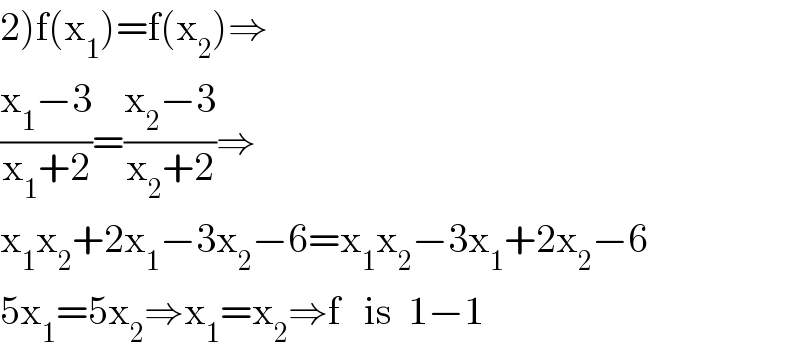
2)f(x_1 )=f(x_2 )⇒ ((x_1 −3)/(x_1 +2))=((x_2 −3)/(x_2 +2))⇒ x_1 x_2 +2x_1 −3x_2 −6=x_1 x_2 −3x_1 +2x_2 −6 5x_1 =5x_2 ⇒x_1 =x_2 ⇒f is 1−1
$$\left.\mathrm{2}\right)\mathrm{f}\left(\mathrm{x}_{\mathrm{1}} \right)=\mathrm{f}\left(\mathrm{x}_{\mathrm{2}} \right)\Rightarrow \\ $$$$\frac{\mathrm{x}_{\mathrm{1}} −\mathrm{3}}{\mathrm{x}_{\mathrm{1}} +\mathrm{2}}=\frac{\mathrm{x}_{\mathrm{2}} −\mathrm{3}}{\mathrm{x}_{\mathrm{2}} +\mathrm{2}}\Rightarrow \\ $$$$\mathrm{x}_{\mathrm{1}} \mathrm{x}_{\mathrm{2}} +\mathrm{2x}_{\mathrm{1}} −\mathrm{3x}_{\mathrm{2}} −\mathrm{6}=\mathrm{x}_{\mathrm{1}} \mathrm{x}_{\mathrm{2}} −\mathrm{3x}_{\mathrm{1}} +\mathrm{2x}_{\mathrm{2}} −\mathrm{6} \\ $$$$\mathrm{5x}_{\mathrm{1}} =\mathrm{5x}_{\mathrm{2}} \Rightarrow\mathrm{x}_{\mathrm{1}} =\mathrm{x}_{\mathrm{2}} \Rightarrow\mathrm{f}\:\:\:\mathrm{is}\:\:\mathrm{1}−\mathrm{1} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *