Question Number 48877 by absa last updated on 29/Nov/18
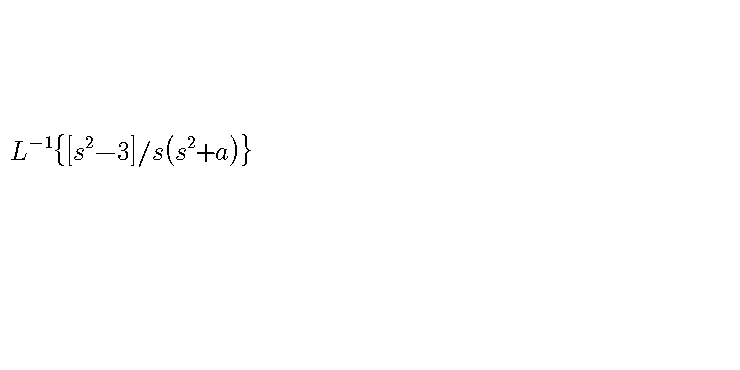
Commented by absa last updated on 29/Nov/18
$${find}\:{the}\:{inverse}\:{laplace}\:{transformation}? \\ $$
Answered by Abdulhafeez Abu qatada last updated on 30/Nov/18

$$\frac{{s}^{\mathrm{2}} −\mathrm{3}}{{s}\left({s}^{\mathrm{2}} +{a}\right)}\:=\:\frac{{A}}{{s}}\:+\:\frac{{Bs}+{C}}{{s}^{\mathrm{2}} +{a}} \\ $$$${s}^{\mathrm{2}} −\mathrm{3}\:=\:{A}\left({s}^{\mathrm{2}} +{a}\right)\:+\:\left({Bs}+{C}\right){s} \\ $$$${s}^{\mathrm{2}} −\mathrm{3}\:=\:\left({A}+{B}\right){s}^{\mathrm{2}} \:+\:{Cs}\:+\:{Aa}\:….{where}\:{a}\:{is}\:{a}\:{constant} \\ $$$${By}\:{comparing}\:{coefficients}, \\ $$$$ \\ $$$${A}\:+\:{B}\:=\:\mathrm{1} \\ $$$${C}\:=\:\mathrm{0} \\ $$$${Aa}\:=\:−\mathrm{3} \\ $$$${C}=\mathrm{0},\:{A}\:=\:\frac{−\mathrm{3}}{{a}},\:{B}\:=\:\mathrm{1}\:−\:\left(\frac{−\mathrm{3}}{{a}}\right)\:=\:\mathrm{1}\:+\:\frac{\mathrm{3}}{{a}}\:=\:\frac{{a}+\mathrm{3}}{{a}} \\ $$$$ \\ $$$$\frac{{s}^{\mathrm{2}} −\mathrm{3}}{{s}\left({s}^{\mathrm{2}} +{a}\right)}\:=\:\frac{−\mathrm{3}}{{as}}\:+\:\frac{\left(\frac{{a}+\mathrm{3}}{{a}}\right){s}}{{s}^{\mathrm{2}} +{a}} \\ $$$${L}^{−\mathrm{1}} \left\{\frac{{s}^{\mathrm{2}} −\mathrm{3}}{{s}\left({s}^{\mathrm{2}} +{a}\right)}\right\}\:=\:{L}^{−\mathrm{1}} \left\{\frac{−\mathrm{3}}{{as}}\:+\:\frac{\left(\frac{{a}+\mathrm{3}}{{a}}\right){s}}{{s}^{\mathrm{2}} +{a}}\right\} \\ $$$${L}^{−\mathrm{1}} \left\{\frac{{s}^{\mathrm{2}} −\mathrm{3}}{{s}\left({s}^{\mathrm{2}} +{a}\right)}\right\}\:=\:\frac{−\mathrm{3}}{{a}}\:+\:\left(\frac{{a}+\mathrm{3}}{{a}}\right){cos}\left(\sqrt{{a}}{t}\right) \\ $$$$ \\ $$
