Menu Close

Question-48879

Tinku Tara 0 Comments
Pin




Question Number 48879 by behi83417@gmail.com last updated on 29/Nov/18
Commented by behi83417@gmail.com last updated on 29/Nov/18
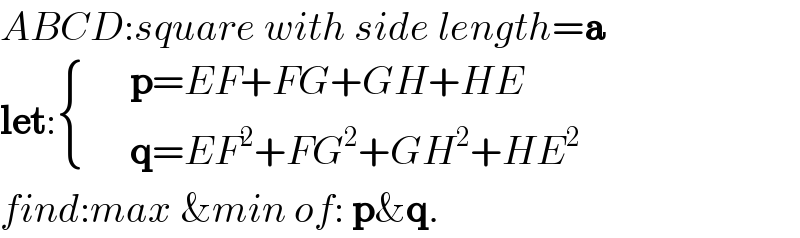
ABCD:square with side length=a let: { (,(p=EF+FG+GH+HE)),(,(q=EF^2 +FG^2 +GH^2 +HE^2 )) :} find:max &min of: p&q.
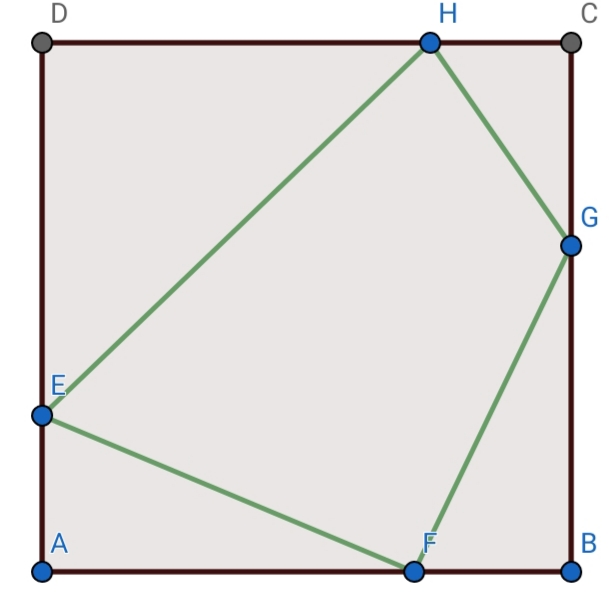
$${ABCD}:{square}\:{with}\:{side}\:{length}=\boldsymbol{\mathrm{a}} \\ $$$$\boldsymbol{\mathrm{let}}:\begin{cases}{}&{\boldsymbol{\mathrm{p}}={EF}+{FG}+{GH}+{HE}}\\{}&{\boldsymbol{\mathrm{q}}={EF}^{\mathrm{2}} +{FG}^{\mathrm{2}} +{GH}^{\mathrm{2}} +{HE}^{\mathrm{2}} }\end{cases} \\ $$$${find}:{max}\:\&{min}\:{of}:\:\boldsymbol{\mathrm{p\&q}}. \\ $$
Commented by ajfour last updated on 29/Nov/18
Commented by mr W last updated on 29/Nov/18
I guess p_(max) ⇒4a p_(min) =2(√2)a q_(max) ⇒4a^2 q_(min) =2a^2
$${I}\:{guess} \\ $$$${p}_{{max}} \Rightarrow\mathrm{4}{a} \\ $$$${p}_{{min}} =\mathrm{2}\sqrt{\mathrm{2}}{a} \\ $$$${q}_{{max}} \Rightarrow\mathrm{4}{a}^{\mathrm{2}} \\ $$$${q}_{{min}} =\mathrm{2}{a}^{\mathrm{2}} \\ $$
Commented by behi83417@gmail.com last updated on 29/Nov/18
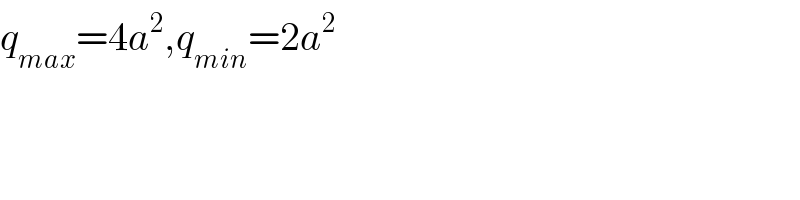
q_(max) =4a^2 ,q_(min) =2a^2
$${q}_{{max}} =\mathrm{4}{a}^{\mathrm{2}} ,{q}_{{min}} =\mathrm{2}{a}^{\mathrm{2}} \\ $$
Commented by behi83417@gmail.com last updated on 29/Nov/18
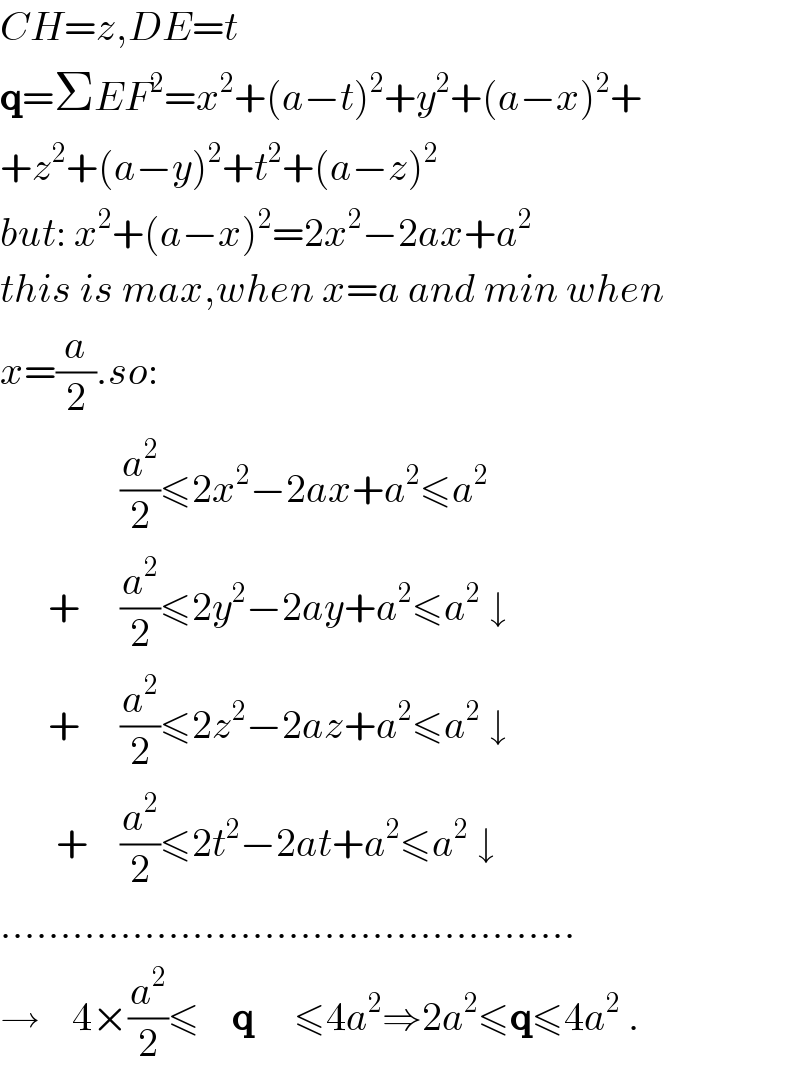
CH=z,DE=t q=ΣEF^2 =x^2 +(a−t)^2 +y^2 +(a−x)^2 + +z^2 +(a−y)^2 +t^2 +(a−z)^2 but: x^2 +(a−x)^2 =2x^2 −2ax+a^2 this is max,when x=a and min when x=(a/2).so: (a^2 /2)≤2x^2 −2ax+a^2 ≤a^2 + (a^2 /2)≤2y^2 −2ay+a^2 ≤a^2 ↓ + (a^2 /2)≤2z^2 −2az+a^2 ≤a^2 ↓ + (a^2 /2)≤2t^2 −2at+a^2 ≤a^2 ↓ ................................................ → 4×(a^2 /2)≤ q ≤4a^2 ⇒2a^2 ≤q≤4a^2 .
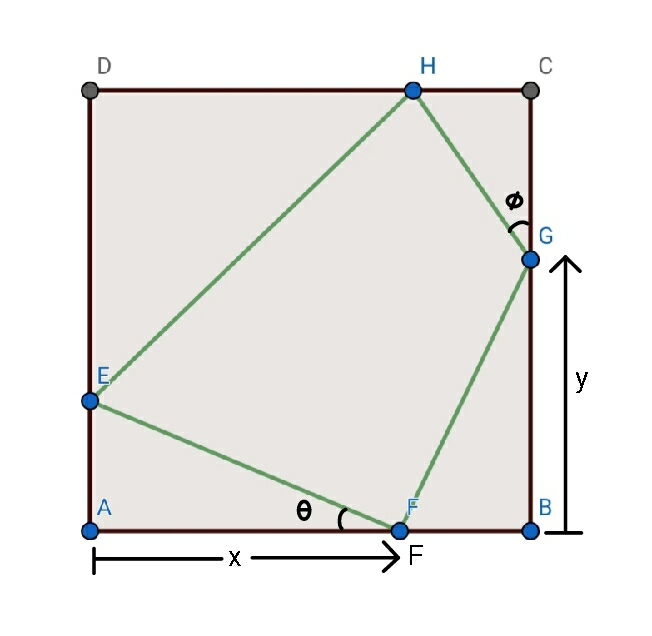
$${CH}={z},{DE}={t} \\ $$$$\boldsymbol{\mathrm{q}}=\Sigma{EF}^{\mathrm{2}} ={x}^{\mathrm{2}} +\left({a}−{t}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} +\left({a}−{x}\right)^{\mathrm{2}} + \\ $$$$+{z}^{\mathrm{2}} +\left({a}−{y}\right)^{\mathrm{2}} +{t}^{\mathrm{2}} +\left({a}−{z}\right)^{\mathrm{2}} \\ $$$${but}:\:{x}^{\mathrm{2}} +\left({a}−{x}\right)^{\mathrm{2}} =\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{ax}+{a}^{\mathrm{2}} \\ $$$${this}\:{is}\:{max},{when}\:{x}={a}\:{and}\:{min}\:{when} \\ $$$${x}=\frac{{a}}{\mathrm{2}}.{so}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\leqslant\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{ax}+{a}^{\mathrm{2}} \leqslant{a}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:+\:\:\:\:\:\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\leqslant\mathrm{2}{y}^{\mathrm{2}} −\mathrm{2}{ay}+{a}^{\mathrm{2}} \leqslant{a}^{\mathrm{2}} \:\downarrow \\ $$$$\:\:\:\:\:\:+\:\:\:\:\:\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\leqslant\mathrm{2}{z}^{\mathrm{2}} −\mathrm{2}{az}+{a}^{\mathrm{2}} \leqslant{a}^{\mathrm{2}} \:\downarrow \\ $$$$\:\:\:\:\:\:\:+\:\:\:\:\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\leqslant\mathrm{2}{t}^{\mathrm{2}} −\mathrm{2}{at}+{a}^{\mathrm{2}} \leqslant{a}^{\mathrm{2}} \:\downarrow \\ $$$$………………………………………… \\ $$$$\rightarrow\:\:\:\:\mathrm{4}×\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\leqslant\:\:\:\:\boldsymbol{\mathrm{q}}\:\:\:\:\:\leqslant\mathrm{4}{a}^{\mathrm{2}} \Rightarrow\mathrm{2}{a}^{\mathrm{2}} \leqslant\boldsymbol{\mathrm{q}}\leqslant\mathrm{4}{a}^{\mathrm{2}} \:.\: \\ $$
Commented by mr W last updated on 29/Nov/18
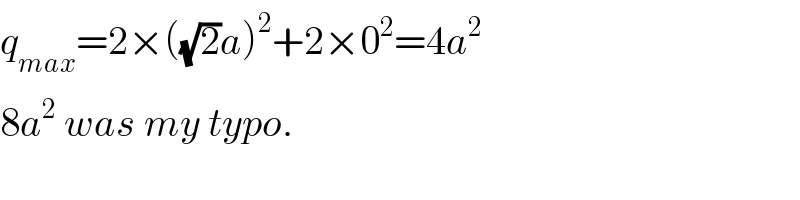
q_(max) =2×((√2)a)^2 +2×0^2 =4a^2 8a^2 was my typo.
$${q}_{{max}} =\mathrm{2}×\left(\sqrt{\mathrm{2}}{a}\right)^{\mathrm{2}} +\mathrm{2}×\mathrm{0}^{\mathrm{2}} =\mathrm{4}{a}^{\mathrm{2}} \\ $$$$\mathrm{8}{a}^{\mathrm{2}} \:{was}\:{my}\:{typo}. \\ $$
Commented by behi83417@gmail.com last updated on 29/Nov/18
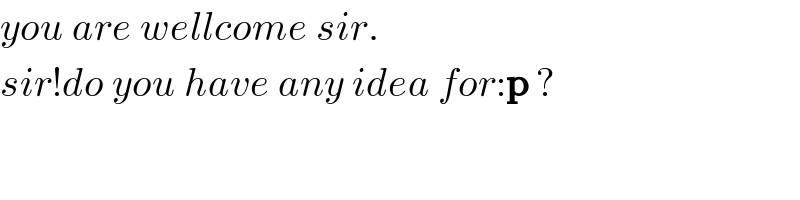
you are wellcome sir. sir!do you have any idea for:p ?
$${you}\:{are}\:{wellcome}\:{sir}. \\ $$$${sir}!{do}\:{you}\:{have}\:{any}\:{idea}\:{for}:\boldsymbol{\mathrm{p}}\:? \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *