Question Number 48899 by behi83417@gmail.com last updated on 29/Nov/18
Commented by behi83417@gmail.com last updated on 29/Nov/18
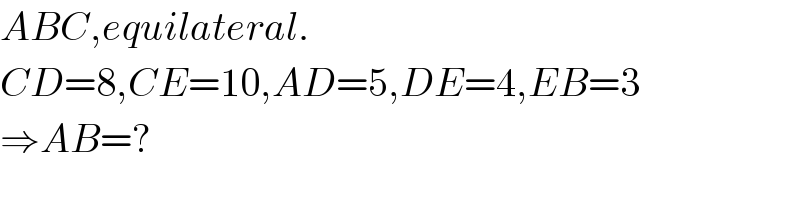
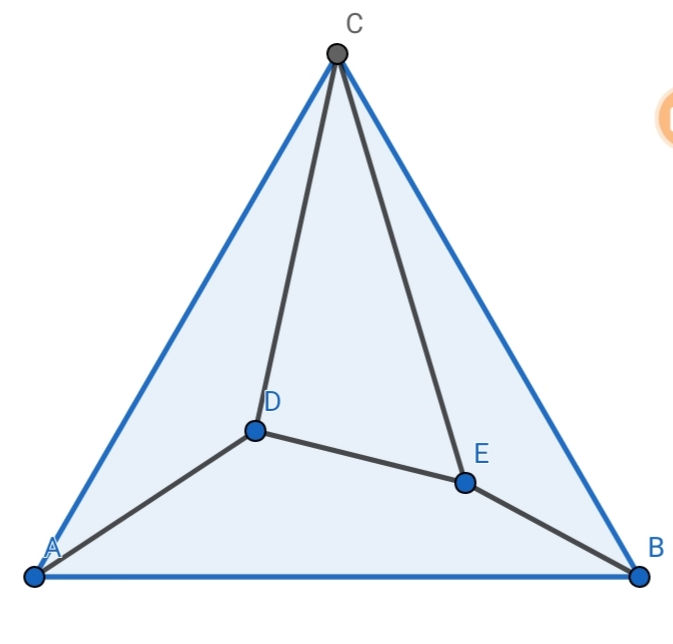
$${ABC},{equilateral}. \\ $$$${CD}=\mathrm{8},{CE}=\mathrm{10},{AD}=\mathrm{5},{DE}=\mathrm{4},{EB}=\mathrm{3} \\ $$$$\Rightarrow{AB}=? \\ $$
Answered by mr W last updated on 30/Nov/18
![let a=side length cos α=((a^2 +8^2 −5^2 )/(2×8×a))=((a^2 +39)/(16a)) cos β=((a^2 +10^2 −3^2 )/(2×10×a))=((a^2 +91)/(20a)) cos γ=((8^2 +10^2 −4^2 )/(2×8×10))=((37)/(40)) ⇒sin α=((√((16a)^2 −(a^2 +39)^2 ))/(16a))=((√((16a+a^2 +39)(16a−a^2 −39)))/(16a)) ⇒sin β=((√((20a)^2 −(a^2 +91)^2 ))/(20a))=((√((20a+a^2 +91)(20a−a^2 −91)))/(20a)) ⇒sin γ=((√(40^2 −37^2 ))/(40))=((√(231))/(40)) α+β+γ=(π/3) α+β=(π/3)−γ cos (α+β)=cos ((π/3)−γ) cos α cos β−sin α sin β=cos (π/3) cos γ+sin (π/3) sin γ ((a^2 +39)/(16a))×((a^2 +91)/(20a))−((√((16a+a^2 +39)(16a−a^2 −39)))/(16a))×((√((20a+a^2 +91)(20a−a^2 −91)))/(20a))=(1/2)×((37)/(40))+((√3)/2)×((√(231))/(40)) (√((16a+a^2 +39)(16a−a^2 −39)(20a+a^2 +91)(20a−a^2 −91)))=(a^2 −39)(a^2 −91)−4a^2 (37+3(√(77))) (16a+a^2 +39)(16a−a^2 −39)(20a+a^2 +91)(20a−a^2 −91)=[(a^2 +39)(a^2 +91)−4a^2 (37+3(√(77)))]^2 we get two positive solutions: a=7.0011 and 11.2719 since a>10 such that D and E lie inside the triangle, ⇒a=11.2719](https://www.tinkutara.com/question/Q48917.png)
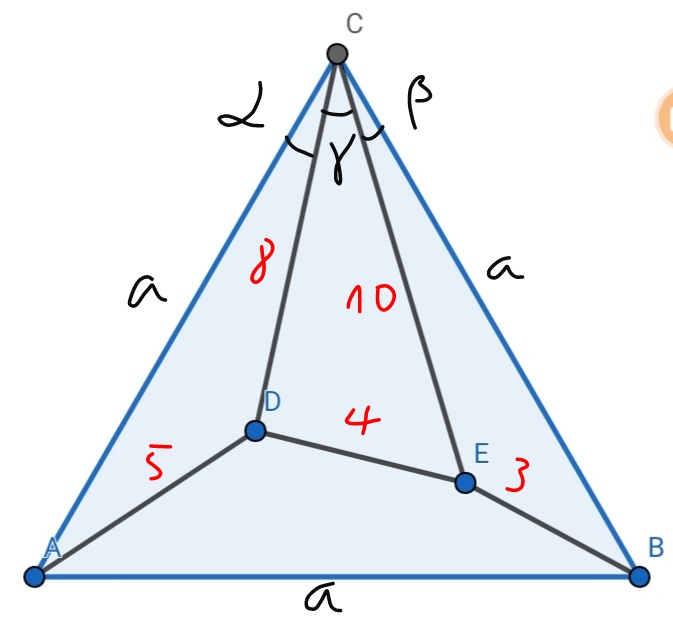
$${let}\:{a}={side}\:{length} \\ $$$$\mathrm{cos}\:\alpha=\frac{{a}^{\mathrm{2}} +\mathrm{8}^{\mathrm{2}} −\mathrm{5}^{\mathrm{2}} }{\mathrm{2}×\mathrm{8}×{a}}=\frac{{a}^{\mathrm{2}} +\mathrm{39}}{\mathrm{16}{a}} \\ $$$$\mathrm{cos}\:\beta=\frac{{a}^{\mathrm{2}} +\mathrm{10}^{\mathrm{2}} −\mathrm{3}^{\mathrm{2}} }{\mathrm{2}×\mathrm{10}×{a}}=\frac{{a}^{\mathrm{2}} +\mathrm{91}}{\mathrm{20}{a}} \\ $$$$\mathrm{cos}\:\gamma=\frac{\mathrm{8}^{\mathrm{2}} +\mathrm{10}^{\mathrm{2}} −\mathrm{4}^{\mathrm{2}} }{\mathrm{2}×\mathrm{8}×\mathrm{10}}=\frac{\mathrm{37}}{\mathrm{40}} \\ $$$$ \\ $$$$\Rightarrow\mathrm{sin}\:\alpha=\frac{\sqrt{\left(\mathrm{16}{a}\right)^{\mathrm{2}} −\left({a}^{\mathrm{2}} +\mathrm{39}\right)^{\mathrm{2}} }}{\mathrm{16}{a}}=\frac{\sqrt{\left(\mathrm{16}{a}+{a}^{\mathrm{2}} +\mathrm{39}\right)\left(\mathrm{16}{a}−{a}^{\mathrm{2}} −\mathrm{39}\right)}}{\mathrm{16}{a}} \\ $$$$\Rightarrow\mathrm{sin}\:\beta=\frac{\sqrt{\left(\mathrm{20}{a}\right)^{\mathrm{2}} −\left({a}^{\mathrm{2}} +\mathrm{91}\right)^{\mathrm{2}} }}{\mathrm{20}{a}}=\frac{\sqrt{\left(\mathrm{20}{a}+{a}^{\mathrm{2}} +\mathrm{91}\right)\left(\mathrm{20}{a}−{a}^{\mathrm{2}} −\mathrm{91}\right)}}{\mathrm{20}{a}} \\ $$$$\Rightarrow\mathrm{sin}\:\gamma=\frac{\sqrt{\mathrm{40}^{\mathrm{2}} −\mathrm{37}^{\mathrm{2}} }}{\mathrm{40}}=\frac{\sqrt{\mathrm{231}}}{\mathrm{40}} \\ $$$$ \\ $$$$\alpha+\beta+\gamma=\frac{\pi}{\mathrm{3}} \\ $$$$\alpha+\beta=\frac{\pi}{\mathrm{3}}−\gamma \\ $$$$\mathrm{cos}\:\left(\alpha+\beta\right)=\mathrm{cos}\:\left(\frac{\pi}{\mathrm{3}}−\gamma\right) \\ $$$$\mathrm{cos}\:\alpha\:\mathrm{cos}\:\beta−\mathrm{sin}\:\alpha\:\mathrm{sin}\:\beta=\mathrm{cos}\:\frac{\pi}{\mathrm{3}}\:\mathrm{cos}\:\gamma+\mathrm{sin}\:\frac{\pi}{\mathrm{3}}\:\mathrm{sin}\:\gamma \\ $$$$\frac{{a}^{\mathrm{2}} +\mathrm{39}}{\mathrm{16}{a}}×\frac{{a}^{\mathrm{2}} +\mathrm{91}}{\mathrm{20}{a}}−\frac{\sqrt{\left(\mathrm{16}{a}+{a}^{\mathrm{2}} +\mathrm{39}\right)\left(\mathrm{16}{a}−{a}^{\mathrm{2}} −\mathrm{39}\right)}}{\mathrm{16}{a}}×\frac{\sqrt{\left(\mathrm{20}{a}+{a}^{\mathrm{2}} +\mathrm{91}\right)\left(\mathrm{20}{a}−{a}^{\mathrm{2}} −\mathrm{91}\right)}}{\mathrm{20}{a}}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{37}}{\mathrm{40}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}×\frac{\sqrt{\mathrm{231}}}{\mathrm{40}} \\ $$$$\sqrt{\left(\mathrm{16}{a}+{a}^{\mathrm{2}} +\mathrm{39}\right)\left(\mathrm{16}{a}−{a}^{\mathrm{2}} −\mathrm{39}\right)\left(\mathrm{20}{a}+{a}^{\mathrm{2}} +\mathrm{91}\right)\left(\mathrm{20}{a}−{a}^{\mathrm{2}} −\mathrm{91}\right)}=\left({a}^{\mathrm{2}} −\mathrm{39}\right)\left({a}^{\mathrm{2}} −\mathrm{91}\right)−\mathrm{4}{a}^{\mathrm{2}} \left(\mathrm{37}+\mathrm{3}\sqrt{\mathrm{77}}\right) \\ $$$$\left(\mathrm{16}{a}+{a}^{\mathrm{2}} +\mathrm{39}\right)\left(\mathrm{16}{a}−{a}^{\mathrm{2}} −\mathrm{39}\right)\left(\mathrm{20}{a}+{a}^{\mathrm{2}} +\mathrm{91}\right)\left(\mathrm{20}{a}−{a}^{\mathrm{2}} −\mathrm{91}\right)=\left[\left({a}^{\mathrm{2}} +\mathrm{39}\right)\left({a}^{\mathrm{2}} +\mathrm{91}\right)−\mathrm{4}{a}^{\mathrm{2}} \left(\mathrm{37}+\mathrm{3}\sqrt{\mathrm{77}}\right)\right]^{\mathrm{2}} \\ $$$${we}\:{get}\:{two}\:{positive}\:{solutions}: \\ $$$${a}=\mathrm{7}.\mathrm{0011}\:{and}\:\mathrm{11}.\mathrm{2719} \\ $$$${since}\:{a}>\mathrm{10}\:{such}\:{that}\:{D}\:{and}\:{E}\:{lie}\:{inside} \\ $$$${the}\:{triangle}, \\ $$$$\Rightarrow{a}=\mathrm{11}.\mathrm{2719} \\ $$
Commented by mr W last updated on 30/Nov/18
Commented by MJS last updated on 30/Nov/18

$$\mathrm{typo}:\:\mathrm{19}{a}^{\mathrm{2}} +\mathrm{91} \\ $$$$\mathrm{mistakes}\:\mathrm{of}\:\mathrm{sign}\:\mathrm{at}\:\mathrm{the}\:\mathrm{beginning}\:{a}^{\mathrm{2}} +\mathrm{8}^{\mathrm{2}} −\mathrm{5}^{\mathrm{2}} = \\ $$$$={a}^{\mathrm{2}} +\mathrm{39}\:… \\ $$
Commented by mr W last updated on 30/Nov/18
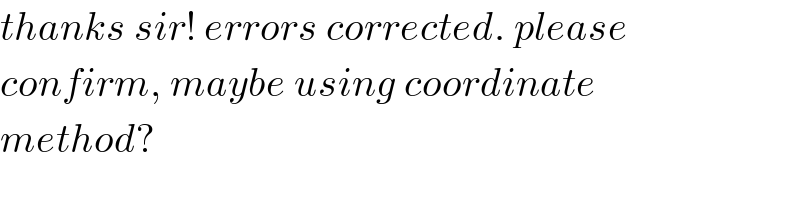
$${thanks}\:{sir}!\:{errors}\:{corrected}.\:{please} \\ $$$${confirm},\:{maybe}\:{using}\:{coordinate}\: \\ $$$${method}? \\ $$
Commented by MJS last updated on 30/Nov/18

$$\mathrm{your}\:\mathrm{method}\:\left(\mathrm{corrected}\right)\:\mathrm{leads}\:\mathrm{to} \\ $$$${a}^{\mathrm{4}} −\frac{\mathrm{6}\left(\mathrm{726}+\mathrm{41}\sqrt{\mathrm{77}}\right)}{\mathrm{37}}{a}^{\mathrm{2}} +\frac{\mathrm{169}\left(\mathrm{93}+\mathrm{2}\sqrt{\mathrm{77}}\right)}{\mathrm{3}}=\mathrm{0} \\ $$$$\Rightarrow\:{a}^{\mathrm{2}} =\frac{\mathrm{2178}+\mathrm{123}\sqrt{\mathrm{77}}}{\mathrm{37}}\pm\frac{\sqrt{−\mathrm{6}\left(\mathrm{1895361}−\mathrm{572321}\sqrt{\mathrm{77}}\right)}}{\mathrm{111}} \\ $$$$\Rightarrow\:{a}\approx\mathrm{7}.\mathrm{00105}\:\vee\:{a}\approx\mathrm{11}.\mathrm{2719} \\ $$$$\mathrm{I}\:\mathrm{got}\:\mathrm{the}\:\mathrm{same}\:\mathrm{result}\:{a}\approx\mathrm{11}.\mathrm{2719} \\ $$
Commented by mr W last updated on 30/Nov/18
Commented by MJS last updated on 30/Nov/18

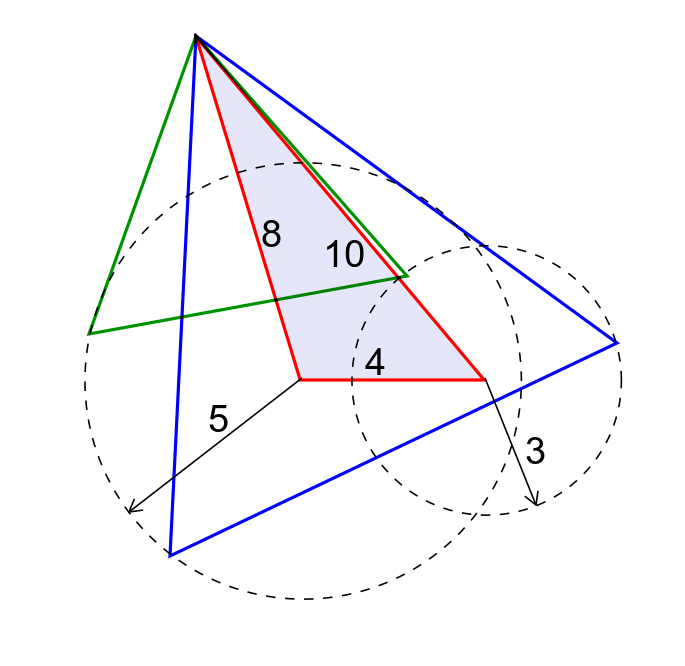
$${a}\approx\mathrm{11}.\mathrm{2719}\:\Rightarrow\:\alpha\approx\mathrm{22}.\mathrm{97}°\:\beta\approx\mathrm{14}.\mathrm{70}°\:\gamma\approx\mathrm{22}.\mathrm{33}° \\ $$$${a}\approx\mathrm{7}.\mathrm{00105}\:\Rightarrow\:\alpha\approx\mathrm{38}.\mathrm{21}°\:\beta\approx−\mathrm{0}.\mathrm{54}°\:\gamma\approx\mathrm{22}.\mathrm{33}° \\ $$$$\:\:\:\:\:\Rightarrow\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{solution}\:\mathrm{means}\:\mathrm{that}\:{D}\:\mathrm{and}\:{E}\:\mathrm{are} \\ $$$$\:\:\:\:\:\mathrm{outside}\:\mathrm{the}\:\mathrm{triangle}\:\left(?\right)\:\mathrm{can}\:\mathrm{you}\:\mathrm{try}\:\mathrm{to} \\ $$$$\:\:\:\:\:\mathrm{draw}\:\mathrm{this}\:\mathrm{situation}? \\ $$$$ \\ $$$$\mathrm{Using}\:\mathrm{coordinate}\:\mathrm{method}\:\mathrm{I}\:\mathrm{made}\:\mathrm{2}\:\mathrm{decisions}: \\ $$$${x}−\mathrm{coordinates}\:\mathrm{of}\:{D}\:\mathrm{is}\:{o}+\sqrt{{p}}\:\mathrm{and}\:{E}\:\mathrm{is}\:{q}−\sqrt{{r}} \\ $$$$\mathrm{to}\:\mathrm{keep}\:\mathrm{both}\:\mathrm{inside}.\:\mathrm{we}\:\mathrm{could}\:\mathrm{get}\:\mathrm{4}\:\mathrm{solutions} \\ $$$$\mathrm{choosing}\:++,\:+−,\:−+,\:−− \\ $$
Commented by MJS last updated on 30/Nov/18
$$\mathrm{thank}\:\mathrm{you}!\:\mathrm{I}\:\mathrm{just}\:\mathrm{tried}\:\mathrm{all}\:\mathrm{4}\:\mathrm{possibilities}\:\mathrm{and} \\ $$$$\mathrm{found}\:\mathrm{in}\:\mathrm{this}\:\mathrm{case}\:\mathrm{we}\:\mathrm{have}\:\mathrm{indeed}\:\mathrm{2}\:\mathrm{solutions} \\ $$
Commented by mr W last updated on 30/Nov/18

$${a}=\mathrm{11}.\mathrm{2719}\:\:{is}\:{for}\:{the}\:{blue}\:{triangle}. \\ $$$${a}=\mathrm{7}.\mathrm{0011}\:{is}\:{for}\:{the}\:{green}\:{one}\:{which} \\ $$$${is}\:{not}\:{the}\:{requested}\:{solution}. \\ $$
Answered by MJS last updated on 30/Nov/18
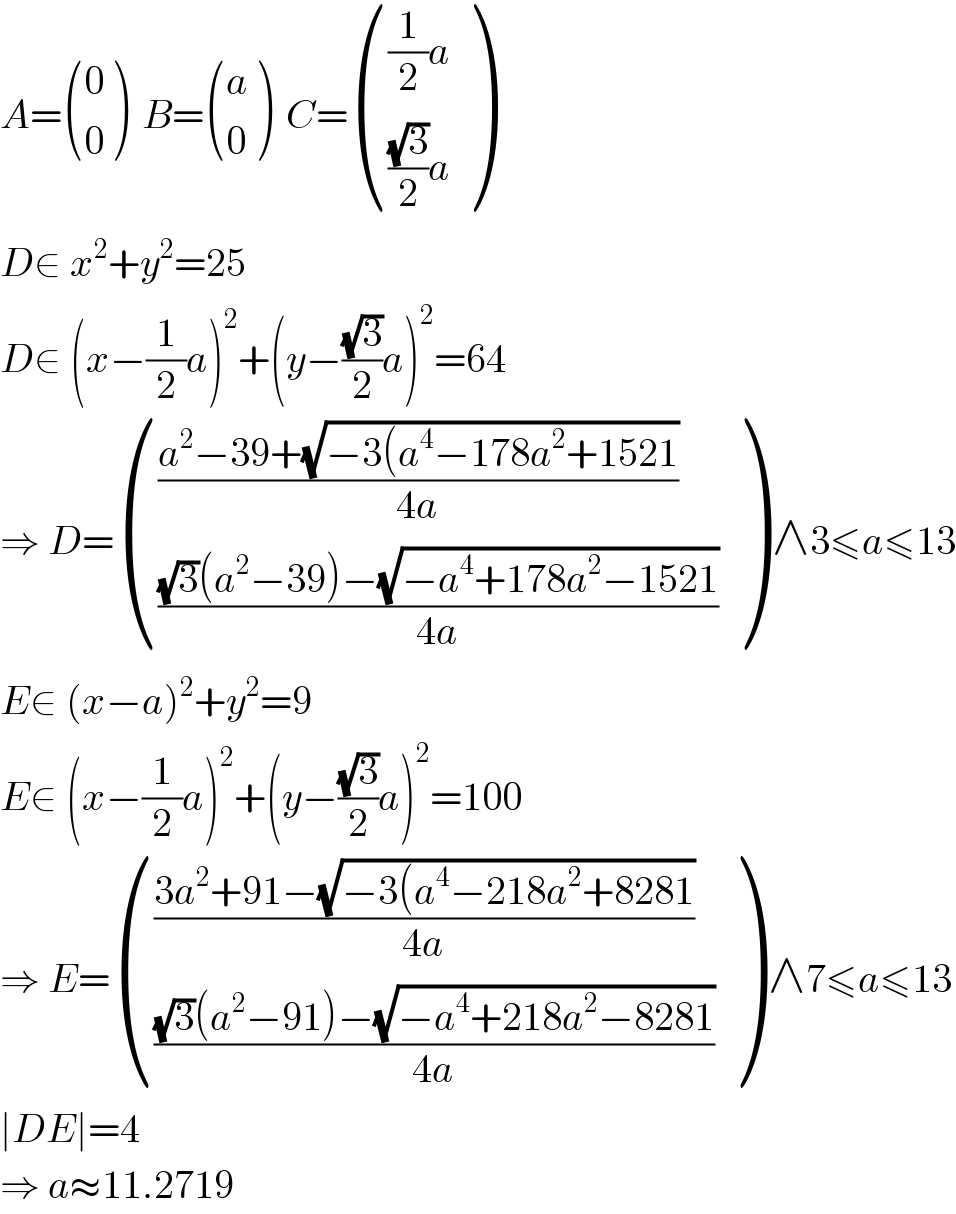
$${A}=\begin{pmatrix}{\mathrm{0}}\\{\mathrm{0}}\end{pmatrix}\:\:{B}=\begin{pmatrix}{{a}}\\{\mathrm{0}}\end{pmatrix}\:\:{C}=\begin{pmatrix}{\frac{\mathrm{1}}{\mathrm{2}}{a}}\\{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{a}}\end{pmatrix} \\ $$$${D}\in\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{25} \\ $$$${D}\in\:\left({x}−\frac{\mathrm{1}}{\mathrm{2}}{a}\right)^{\mathrm{2}} +\left({y}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{a}\right)^{\mathrm{2}} =\mathrm{64} \\ $$$$\Rightarrow\:{D}=\begin{pmatrix}{\frac{{a}^{\mathrm{2}} −\mathrm{39}+\sqrt{−\mathrm{3}\left({a}^{\mathrm{4}} −\mathrm{178}{a}^{\mathrm{2}} +\mathrm{1521}\right.}}{\mathrm{4}{a}}}\\{\frac{\sqrt{\mathrm{3}}\left({a}^{\mathrm{2}} −\mathrm{39}\right)−\sqrt{−{a}^{\mathrm{4}} +\mathrm{178}{a}^{\mathrm{2}} −\mathrm{1521}}}{\mathrm{4}{a}}}\end{pmatrix}\:\wedge\mathrm{3}\leqslant{a}\leqslant\mathrm{13} \\ $$$${E}\in\:\left({x}−{a}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{9} \\ $$$${E}\in\:\left({x}−\frac{\mathrm{1}}{\mathrm{2}}{a}\right)^{\mathrm{2}} +\left({y}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{a}\right)^{\mathrm{2}} =\mathrm{100} \\ $$$$\Rightarrow\:{E}=\begin{pmatrix}{\frac{\mathrm{3}{a}^{\mathrm{2}} +\mathrm{91}−\sqrt{−\mathrm{3}\left({a}^{\mathrm{4}} −\mathrm{218}{a}^{\mathrm{2}} +\mathrm{8281}\right.}}{\mathrm{4}{a}}}\\{\frac{\sqrt{\mathrm{3}}\left({a}^{\mathrm{2}} −\mathrm{91}\right)−\sqrt{−{a}^{\mathrm{4}} +\mathrm{218}{a}^{\mathrm{2}} −\mathrm{8281}}}{\mathrm{4}{a}}}\end{pmatrix}\:\wedge\mathrm{7}\leqslant{a}\leqslant\mathrm{13} \\ $$$$\mid{DE}\mid=\mathrm{4} \\ $$$$\Rightarrow\:{a}\approx\mathrm{11}.\mathrm{2719} \\ $$
Commented by behi83417@gmail.com last updated on 30/Nov/18
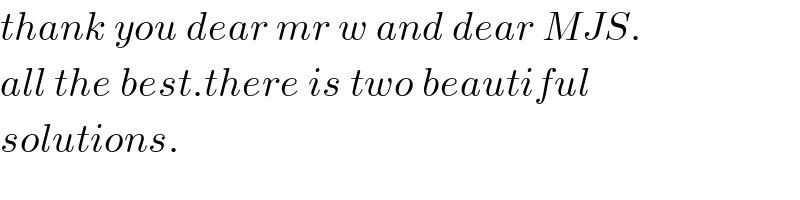
$${thank}\:{you}\:{dear}\:{mr}\:{w}\:{and}\:{dear}\:{MJS}. \\ $$$${all}\:{the}\:{best}.{there}\:{is}\:{two}\:{beautiful}\: \\ $$$${solutions}. \\ $$
