Question Number 48952 by somil last updated on 30/Nov/18
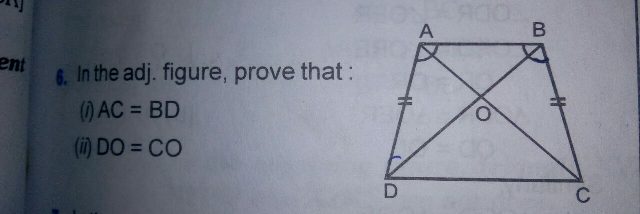
Answered by $@ty@m last updated on 01/Dec/18
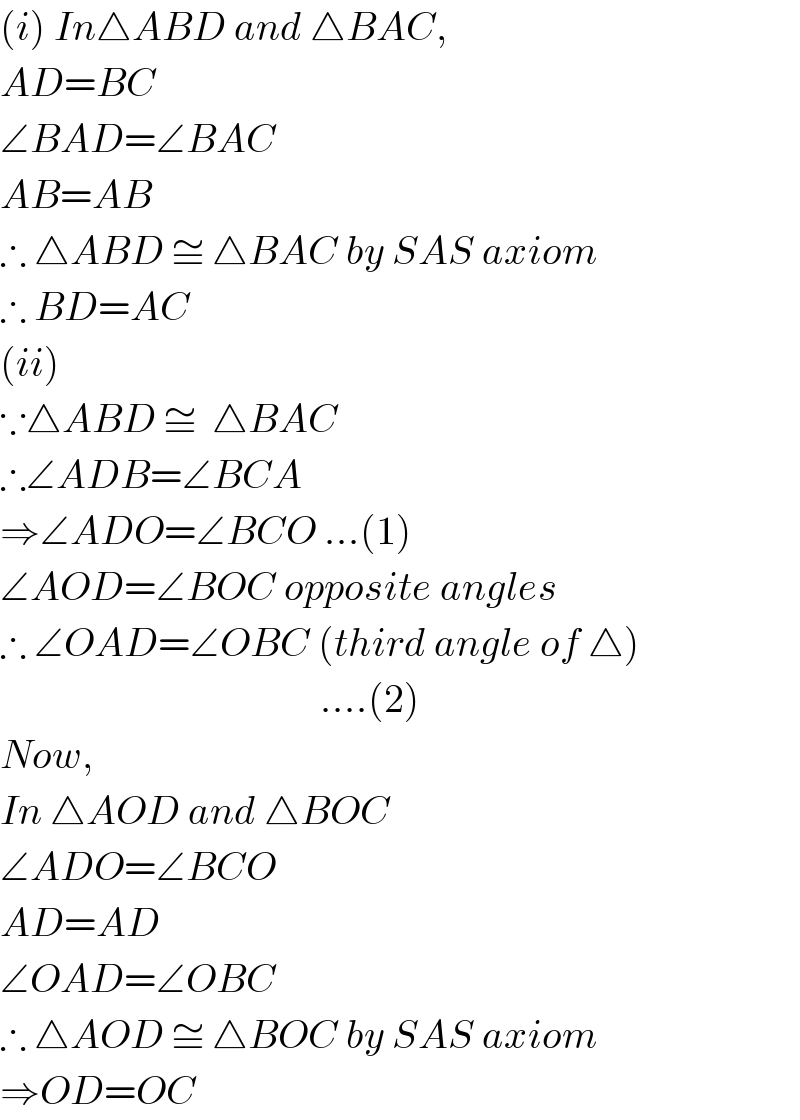
$$\left({i}\right)\:{In}\bigtriangleup{ABD}\:{and}\:\bigtriangleup{BAC}, \\ $$$${AD}={BC} \\ $$$$\angle{BAD}=\angle{BAC} \\ $$$${AB}={AB} \\ $$$$\therefore\:\bigtriangleup{ABD}\:\cong\:\bigtriangleup{BAC}\:{by}\:{SAS}\:{axiom} \\ $$$$\therefore\:{BD}={AC} \\ $$$$\left({ii}\right) \\ $$$$\because\bigtriangleup{ABD}\:\cong\:\:\bigtriangleup{BAC} \\ $$$$\therefore\angle{ADB}=\angle{BCA}\: \\ $$$$\Rightarrow\angle{ADO}=\angle{BCO}\:…\left(\mathrm{1}\right) \\ $$$$\angle{AOD}=\angle{BOC}\:{opposite}\:{angles} \\ $$$$\therefore\:\angle{OAD}=\angle{OBC}\:\left({third}\:{angle}\:{of}\:\bigtriangleup\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:….\left(\mathrm{2}\right) \\ $$$${Now}, \\ $$$${In}\:\bigtriangleup{AOD}\:{and}\:\bigtriangleup{BOC} \\ $$$$\angle{ADO}=\angle{BCO}\: \\ $$$${AD}={AD} \\ $$$$\angle{OAD}=\angle{OBC} \\ $$$$\therefore\:\bigtriangleup{AOD}\:\cong\:\bigtriangleup{BOC}\:{by}\:{SAS}\:{axiom} \\ $$$$\Rightarrow{OD}={OC} \\ $$
