Question Number 48981 by peter frank last updated on 30/Nov/18

Answered by tanmay.chaudhury50@gmail.com last updated on 01/Dec/18
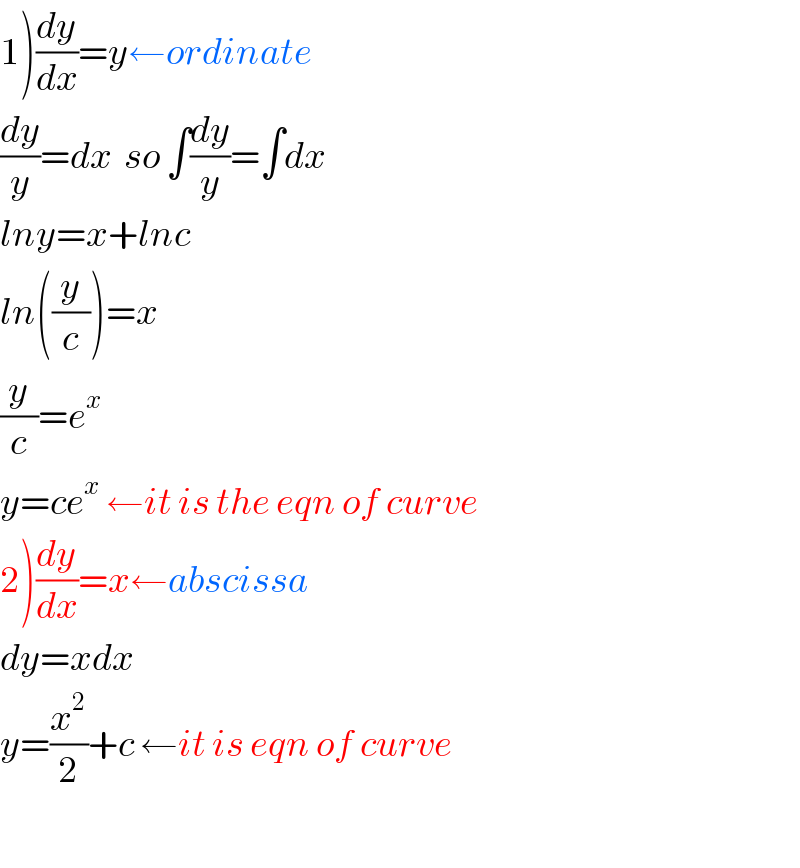
$$\left.\mathrm{1}\right)\frac{{dy}}{{dx}}={y}\leftarrow{ordinate} \\ $$$$\frac{{dy}}{{y}}={dx}\:\:{so}\:\int\frac{{dy}}{{y}}=\int{dx} \\ $$$${lny}={x}+{lnc} \\ $$$${ln}\left(\frac{{y}}{{c}}\right)={x} \\ $$$$\frac{{y}}{{c}}={e}^{{x}} \\ $$$${y}={ce}^{{x}} \:\leftarrow{it}\:{is}\:{the}\:{eqn}\:{of}\:{curve} \\ $$$$\left.\mathrm{2}\right)\frac{{dy}}{{dx}}={x}\leftarrow{abscissa} \\ $$$${dy}={xdx} \\ $$$${y}=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{c}\:\leftarrow{it}\:{is}\:{eqn}\:{of}\:{curve} \\ $$$$ \\ $$
