Question Number 48982 by peter frank last updated on 30/Nov/18
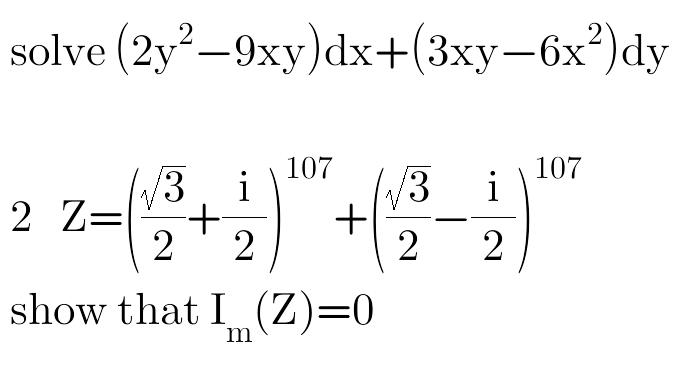
Answered by tanmay.chaudhury50@gmail.com last updated on 01/Dec/18

$$\left.\mathrm{2}\right)\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}={sin}\left(\frac{\pi}{\mathrm{6}}\right)\:\:\:\frac{\mathrm{1}}{\mathrm{2}}={cos}\left(\frac{\pi}{\mathrm{6}}\right) \\ $$$${e}^{{i}\theta} ={cos}\theta+{isin}\theta\:\leftarrow{demoivers}\:{theorem} \\ $$$${e}^{−{i}\theta} ={cos}\theta−{isin}\theta \\ $$$${z}=\left({e}^{{i}\frac{\pi}{\mathrm{6}}} \right)^{\mathrm{107}} +\left({e}^{{i}\frac{−\pi}{\mathrm{6}}} \right)^{\mathrm{107}} \\ $$$$={e}^{{i}\frac{\mathrm{107}\pi}{\mathrm{6}}} +{e}^{−{i}\frac{\mathrm{107}\pi}{\mathrm{6}}} \\ $$$$=\left({cos}\frac{\mathrm{107}\pi}{\mathrm{6}}+{isin}\frac{\mathrm{107}\pi}{\mathrm{6}}\right)+\left({cos}\frac{\mathrm{107}\pi}{\mathrm{6}}−{isin}\frac{\mathrm{107}\pi}{\mathrm{6}}\right) \\ $$$$=\mathrm{2}{cos}\left(\frac{\mathrm{107}\pi}{\mathrm{6}}\right)+{i}\left(\mathrm{0}\right) \\ $$$${so}\:{I}_{{m}} \left({Z}\right)=\mathrm{0} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 01/Dec/18

$$\left.\mathrm{1}\right){question}\:{incomplete} \\ $$$$ \\ $$
