Menu Close

Question-48983

Tinku Tara 0 Comments
Pin




Question Number 48983 by peter frank last updated on 30/Nov/18
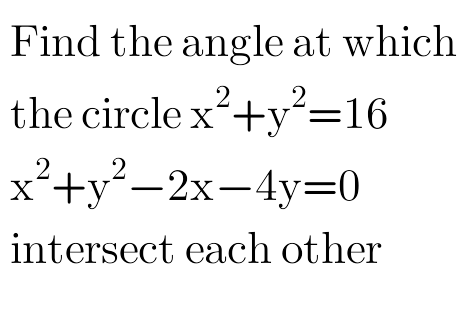
Answered by tanmay.chaudhury50@gmail.com last updated on 01/Dec/18
(x−0)^2 +(y−0)^2 =4^2 x^2 −2x+1+y^2 −4y+4=5 (x−1)^2 +(y−2)^2 =((√5) )^2 solving to find points of intersects 16−2x−4y=0 8−x−2y=0 x=8−2y (8−2y)^2 +y^2 =16 64−32y+5y^2 −16=0 5y^2 −32y+48=0 5y^2 −20y−12y+48=0 5y(y−4)−12(y−4)=0 (y−4)(5y−12)=0 y=4 and x=0 y=((12)/5) x=8−((24)/5)=((16)/5) (0,4) and(((16)/5),((12)/5)) are the points of intersection of two circles tangents at (0,4) for circle x^2 +y^2 =16 is x×0+y×4=16 y=4 is a st line parallel to x axis so slope m_1 =0 tangents at(0,4) for circle x^2 +y^2 −2x−4y=0 x×0+y×4−(x+0)−2(y+4)=0 4y−x−2y−4=0 2y=x+4 y=(x/2)+2 so slope m_2 =(1/2) now angle between two circles at point (0,4) tanθ_1 =(((1/(2 ))−0)/(1+(1/2)×0))=(1/2) formula tanθ=((m_1 ∼m_2 )/(1+m_1 m_2 )) so θ_1 =tan^(−1) ((1/(2 ))) tangents at(((16)/5),((12)/5)) for circle x^2 +y^2 =16 x×((16)/5)+y×((12)/5)=16 4(4x+3y)=16×5 4x+3y=20 m_1 =((−4)/3) tangent at(((16)/5),((12)/5)) for circle x^2 +y^2 −2x−4y=0 x×((16)/5)+y×((12)/5)−(x+((16)/5))−2(y+((12)/5))=0 16x+12y−5x−16−10y−24=0 2y+11x=40 m_2 =((−11)/2) tanθ_2 =((((−4)/3)+((11)/2))/(1+((−11)/2)×((−4)/3))).=(((−8+33)/6)/((6+44)/6))=((25)/(50))=(1/2) θ_2 =tan^(−1) ((1/2))
$$\left({x}−\mathrm{0}\right)^{\mathrm{2}} +\left({y}−\mathrm{0}\right)^{\mathrm{2}} =\mathrm{4}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}+{y}^{\mathrm{2}} −\mathrm{4}{y}+\mathrm{4}=\mathrm{5} \\ $$$$\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\left({y}−\mathrm{2}\right)^{\mathrm{2}} =\left(\sqrt{\mathrm{5}}\:\right)^{\mathrm{2}} \\ $$$${solving}\:{to}\:{find}\:{points}\:{of}\:{intersects} \\ $$$$\mathrm{16}−\mathrm{2}{x}−\mathrm{4}{y}=\mathrm{0} \\ $$$$\mathrm{8}−{x}−\mathrm{2}{y}=\mathrm{0} \\ $$$${x}=\mathrm{8}−\mathrm{2}{y} \\ $$$$\left(\mathrm{8}−\mathrm{2}{y}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{16} \\ $$$$\mathrm{64}−\mathrm{32}{y}+\mathrm{5}{y}^{\mathrm{2}} −\mathrm{16}=\mathrm{0} \\ $$$$\mathrm{5}{y}^{\mathrm{2}} −\mathrm{32}{y}+\mathrm{48}=\mathrm{0} \\ $$$$\mathrm{5}{y}^{\mathrm{2}} −\mathrm{20}{y}−\mathrm{12}{y}+\mathrm{48}=\mathrm{0} \\ $$$$\mathrm{5}{y}\left({y}−\mathrm{4}\right)−\mathrm{12}\left({y}−\mathrm{4}\right)=\mathrm{0} \\ $$$$\left({y}−\mathrm{4}\right)\left(\mathrm{5}{y}−\mathrm{12}\right)=\mathrm{0} \\ $$$${y}=\mathrm{4}\:\:{and}\:{x}=\mathrm{0} \\ $$$${y}=\frac{\mathrm{12}}{\mathrm{5}}\:\:\:{x}=\mathrm{8}−\frac{\mathrm{24}}{\mathrm{5}}=\frac{\mathrm{16}}{\mathrm{5}} \\ $$$$\left(\mathrm{0},\mathrm{4}\right)\:{and}\left(\frac{\mathrm{16}}{\mathrm{5}},\frac{\mathrm{12}}{\mathrm{5}}\right)\:{are}\:{the}\:{points}\:{of}\:{intersection} \\ $$$${of}\:{two}\:{circles} \\ $$$${tangents}\:{at}\:\left(\mathrm{0},\mathrm{4}\right)\:{for}\:{circle}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{16} \\ $$$${is}\:{x}×\mathrm{0}+{y}×\mathrm{4}=\mathrm{16} \\ $$$${y}=\mathrm{4}\:{is}\:{a}\:{st}\:{line}\:{parallel}\:{to}\:{x}\:{axis}\:{so}\:{slope}\:{m}_{\mathrm{1}} =\mathrm{0} \\ $$$${tangents}\:{at}\left(\mathrm{0},\mathrm{4}\right)\:{for}\:{circle}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{4}{y}=\mathrm{0} \\ $$$${x}×\mathrm{0}+{y}×\mathrm{4}−\left({x}+\mathrm{0}\right)−\mathrm{2}\left({y}+\mathrm{4}\right)=\mathrm{0} \\ $$$$\mathrm{4}{y}−{x}−\mathrm{2}{y}−\mathrm{4}=\mathrm{0} \\ $$$$\mathrm{2}{y}={x}+\mathrm{4} \\ $$$${y}=\frac{{x}}{\mathrm{2}}+\mathrm{2}\:\:{so}\:{slope}\:{m}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${now}\:{angle}\:{between}\:{two}\:{circles}\:{at}\:{point}\:\left(\mathrm{0},\mathrm{4}\right) \\ $$$${tan}\theta_{\mathrm{1}} =\frac{\frac{\mathrm{1}}{\mathrm{2}\:}−\mathrm{0}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{0}}=\frac{\mathrm{1}}{\mathrm{2}}\:{formula}\:{tan}\theta=\frac{{m}_{\mathrm{1}} \sim{m}_{\mathrm{2}} }{\mathrm{1}+{m}_{\mathrm{1}} {m}_{\mathrm{2}} } \\ $$$${so}\:\theta_{\mathrm{1}} ={tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}\:}\right) \\ $$$$ \\ $$$$ \\ $$$${tangents}\:{at}\left(\frac{\mathrm{16}}{\mathrm{5}},\frac{\mathrm{12}}{\mathrm{5}}\right)\:{for}\:{circle}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{16} \\ $$$${x}×\frac{\mathrm{16}}{\mathrm{5}}+{y}×\frac{\mathrm{12}}{\mathrm{5}}=\mathrm{16} \\ $$$$\mathrm{4}\left(\mathrm{4}{x}+\mathrm{3}{y}\right)=\mathrm{16}×\mathrm{5} \\ $$$$\mathrm{4}{x}+\mathrm{3}{y}=\mathrm{20}\:\:\:{m}_{\mathrm{1}} =\frac{−\mathrm{4}}{\mathrm{3}} \\ $$$${tangent}\:{at}\left(\frac{\mathrm{16}}{\mathrm{5}},\frac{\mathrm{12}}{\mathrm{5}}\right)\:{for}\:{circle}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{4}{y}=\mathrm{0} \\ $$$${x}×\frac{\mathrm{16}}{\mathrm{5}}+{y}×\frac{\mathrm{12}}{\mathrm{5}}−\left({x}+\frac{\mathrm{16}}{\mathrm{5}}\right)−\mathrm{2}\left({y}+\frac{\mathrm{12}}{\mathrm{5}}\right)=\mathrm{0} \\ $$$$\mathrm{16}{x}+\mathrm{12}{y}−\mathrm{5}{x}−\mathrm{16}−\mathrm{10}{y}−\mathrm{24}=\mathrm{0} \\ $$$$\mathrm{2}{y}+\mathrm{11}{x}=\mathrm{40} \\ $$$${m}_{\mathrm{2}} =\frac{−\mathrm{11}}{\mathrm{2}} \\ $$$${tan}\theta_{\mathrm{2}} =\frac{\frac{−\mathrm{4}}{\mathrm{3}}+\frac{\mathrm{11}}{\mathrm{2}}}{\mathrm{1}+\frac{−\mathrm{11}}{\mathrm{2}}×\frac{−\mathrm{4}}{\mathrm{3}}}.=\frac{\frac{−\mathrm{8}+\mathrm{33}}{\mathrm{6}}}{\frac{\mathrm{6}+\mathrm{44}}{\mathrm{6}}}=\frac{\mathrm{25}}{\mathrm{50}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\theta_{\mathrm{2}} ={tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *