Question Number 49014 by peter frank last updated on 01/Dec/18

Commented by peter frank last updated on 01/Dec/18

$$\mathrm{7b}\:\mathrm{8a}\:\mathrm{8b} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 01/Dec/18

$$\left.\mathrm{7}{b}\right){total}\:{surface}\:{arra}\:{of}\:{cone} \\ $$$$={curved}\:{suface}\:{area}+{circular}\:{base}\:{area} \\ $$$$=\pi{rl}+\pi{r}^{\mathrm{2}} \\ $$$$=\pi{r}\left({l}+{r}\right) \\ $$$$=\pi\left(\frac{{d}}{\mathrm{2}}\right)\left({l}+\frac{{d}}{\mathrm{2}}\right) \\ $$$$=\pi\left(\frac{{d}}{\mathrm{2}}\right)×\frac{{d}}{\mathrm{2}}\left(\mathrm{1}+{l}×\frac{\mathrm{2}}{{d}}\right) \\ $$$$=\pi\left(\frac{{d}^{\mathrm{2}} }{\mathrm{4}}\right)\left(\mathrm{1}+\frac{\mathrm{2}{l}}{{d}}\right) \\ $$$$ \\ $$$${proof}\:.. \\ $$$${curved}\:{surface}\:{area}\:{of}\:{cone}=\pi{rl} \\ $$$${if}\:{you}\:{cut}\:{cone}\:{you}\:{get}\:{a}\:{semi}\:{circle}.. \\ $$$${slant}\:{height}\:{of}\:{cone}\:{becomes}\:{the}\:{radius}\:{of} \\ $$$${semicircle} \\ $$$${so}\:{l}={r}_{{circle}} \\ $$$$\mathrm{2}\pi{r}_{{cone}} =\pi{r}_{{circle}} \\ $$$$\mathrm{2}{r}_{{cone}\:} ={r}_{{circle}} \\ $$$${area}\:{of}\:{semicircle}={slant}\:{surface}\:{area}\:{of}\:{cone} \\ $$$$\frac{\pi{r}_{{circle}} ^{\mathrm{2}} }{\mathrm{2}}={slan}\:{surface}\:{area}\:{of}\:{cone} \\ $$$$=\frac{\pi{r}_{{circle}} ×{r}_{{circle}} }{\mathrm{2}} \\ $$$$=\frac{\pi×\mathrm{2}{r}_{{cone}} ×{l}}{\mathrm{2}} \\ $$$$=\frac{\pi×{d}_{{cone}} ×{l}}{\mathrm{2}} \\ $$$${pls}\:{wait}\:{i}\:{am}\:{attaching}\:{picture}… \\ $$$$ \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 01/Dec/18

Commented by peter frank last updated on 01/Dec/18
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{sir} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 01/Dec/18

$$\left.\mathrm{8}{a}\right)\pi{r}^{\mathrm{2}} {h}−\frac{\mathrm{1}}{\mathrm{3}}\pi{r}^{\mathrm{2}} {h} \\ $$
Commented by peter frank last updated on 01/Dec/18
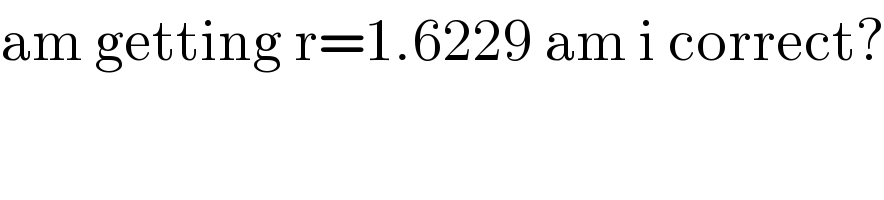
$$\mathrm{am}\:\mathrm{getting}\:\mathrm{r}=\mathrm{1}.\mathrm{6229}\:\mathrm{am}\:\mathrm{i}\:\mathrm{correct}? \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 01/Dec/18

$$\left.{in}\:{question}\:\mathrm{8}{a}\right)\:{no}\:{dimension}\:{is}\:{given}\:{in} \\ $$$${figure}\:…{so}\:{no}\:{comments}… \\ $$
Commented by peter frank last updated on 01/Dec/18
$$\mathrm{okay}\:\mathrm{sir}\:\mathrm{thanks} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 01/Dec/18
![8b)total surface area of cylinder 2πrh+πr^2 +πr^2 2πr(h+r) C_(b ) (h+r) [C_b =2πr] 2πrh→curved surface area πr^2 +πr^2 →for two circular area](https://www.tinkutara.com/question/Q49023.png)
$$\left.\mathrm{8}{b}\right){total}\:{surface}\:{area}\:{of}\:{cylinder} \\ $$$$\mathrm{2}\pi{rh}+\pi{r}^{\mathrm{2}} +\pi{r}^{\mathrm{2}} \\ $$$$\mathrm{2}\pi{r}\left({h}+{r}\right) \\ $$$${C}_{{b}\:} \left({h}+{r}\right)\:\:\left[{C}_{{b}} =\mathrm{2}\pi{r}\right] \\ $$$$\mathrm{2}\pi{rh}\rightarrow{curved}\:{surface}\:{area} \\ $$$$\pi{r}^{\mathrm{2}} +\pi{r}^{\mathrm{2}} \rightarrow{for}\:{two}\:{circular}\:{area} \\ $$$$ \\ $$
