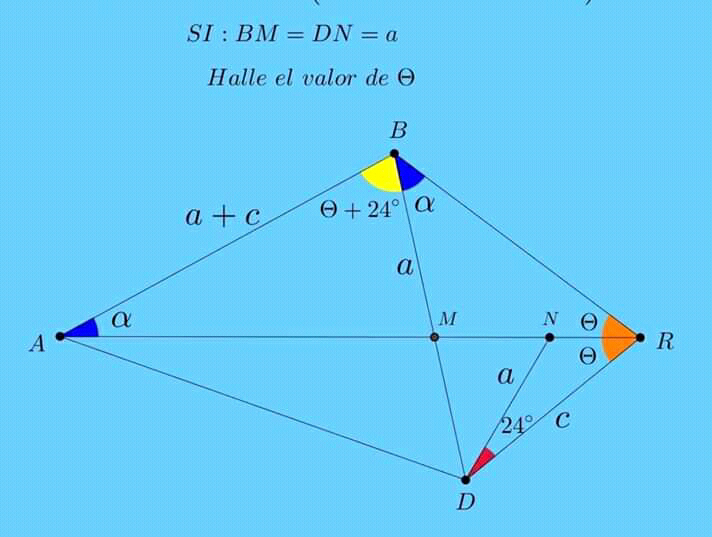
Question Number 49060 by Pk1167156@gmail.com last updated on 02/Dec/18
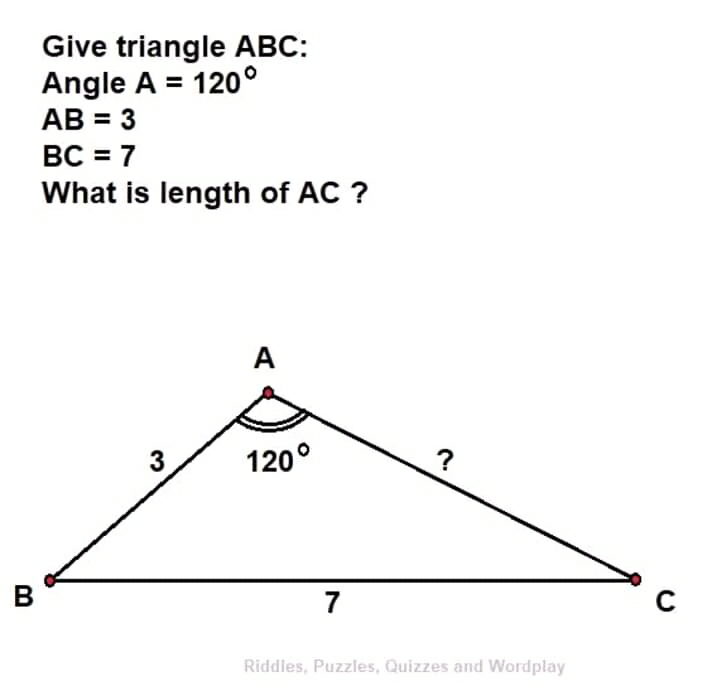
Answered by mr W last updated on 02/Dec/18
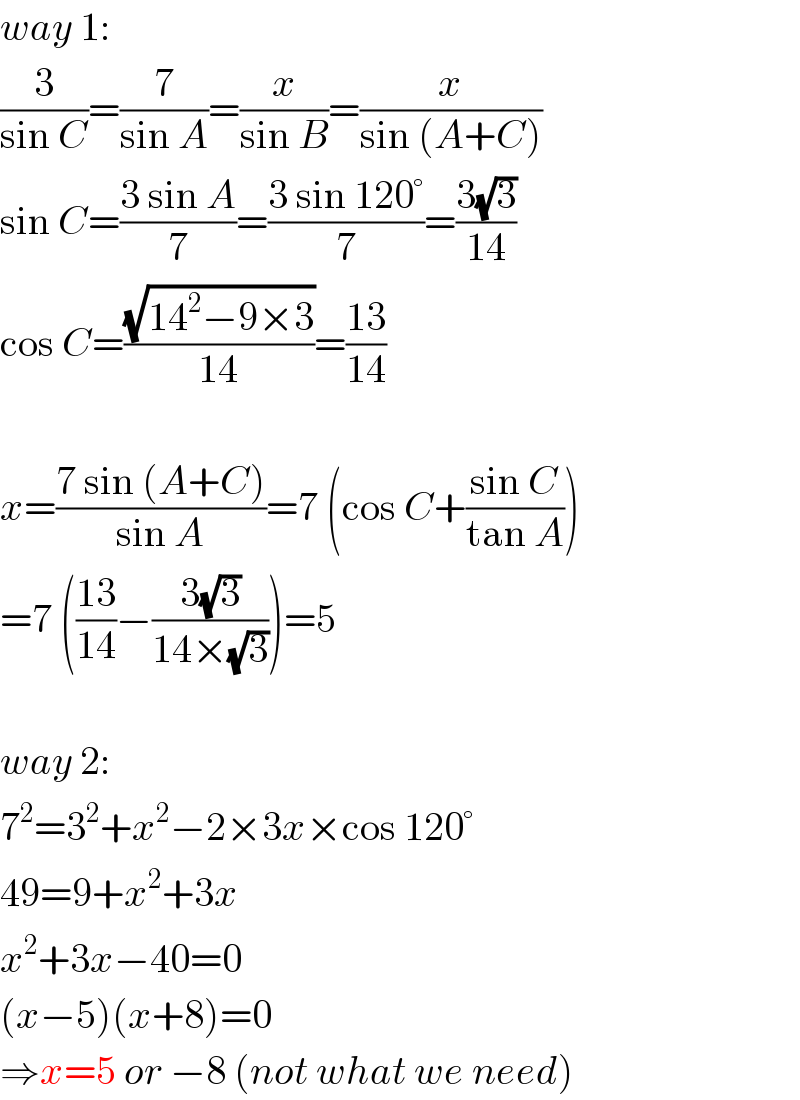
$${way}\:\mathrm{1}: \\ $$$$\frac{\mathrm{3}}{\mathrm{sin}\:{C}}=\frac{\mathrm{7}}{\mathrm{sin}\:{A}}=\frac{{x}}{\mathrm{sin}\:{B}}=\frac{{x}}{\mathrm{sin}\:\left({A}+{C}\right)} \\ $$$$\mathrm{sin}\:{C}=\frac{\mathrm{3}\:\mathrm{sin}\:{A}}{\mathrm{7}}=\frac{\mathrm{3}\:\mathrm{sin}\:\mathrm{120}°}{\mathrm{7}}=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{14}} \\ $$$$\mathrm{cos}\:{C}=\frac{\sqrt{\mathrm{14}^{\mathrm{2}} −\mathrm{9}×\mathrm{3}}}{\mathrm{14}}=\frac{\mathrm{13}}{\mathrm{14}} \\ $$$$ \\ $$$${x}=\frac{\mathrm{7}\:\mathrm{sin}\:\left({A}+{C}\right)}{\mathrm{sin}\:{A}}=\mathrm{7}\:\left(\mathrm{cos}\:{C}+\frac{\mathrm{sin}\:{C}}{\mathrm{tan}\:{A}}\right) \\ $$$$=\mathrm{7}\:\left(\frac{\mathrm{13}}{\mathrm{14}}−\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{14}×\sqrt{\mathrm{3}}}\right)=\mathrm{5} \\ $$$$ \\ $$$${way}\:\mathrm{2}: \\ $$$$\mathrm{7}^{\mathrm{2}} =\mathrm{3}^{\mathrm{2}} +{x}^{\mathrm{2}} −\mathrm{2}×\mathrm{3}{x}×\mathrm{cos}\:\mathrm{120}° \\ $$$$\mathrm{49}=\mathrm{9}+{x}^{\mathrm{2}} +\mathrm{3}{x} \\ $$$${x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{40}=\mathrm{0} \\ $$$$\left({x}−\mathrm{5}\right)\left({x}+\mathrm{8}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}=\mathrm{5}\:{or}\:−\mathrm{8}\:\left({not}\:{what}\:{we}\:{need}\right) \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 02/Dec/18
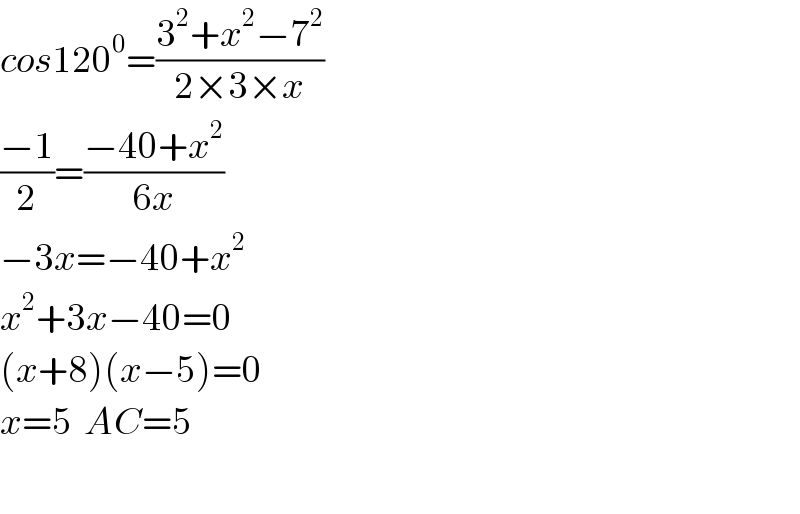
$${cos}\mathrm{120}^{\mathrm{0}} =\frac{\mathrm{3}^{\mathrm{2}} +{x}^{\mathrm{2}} −\mathrm{7}^{\mathrm{2}} }{\mathrm{2}×\mathrm{3}×{x}} \\ $$$$\frac{−\mathrm{1}}{\mathrm{2}}=\frac{−\mathrm{40}+{x}^{\mathrm{2}} }{\mathrm{6}{x}} \\ $$$$−\mathrm{3}{x}=−\mathrm{40}+{x}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{40}=\mathrm{0} \\ $$$$\left({x}+\mathrm{8}\right)\left({x}−\mathrm{5}\right)=\mathrm{0} \\ $$$${x}=\mathrm{5}\:\:{AC}=\mathrm{5} \\ $$$$ \\ $$
Commented by Pk1167156@gmail.com last updated on 02/Dec/18